---

半角公式

$\sin \frac{\alpha }{2}=\pm \sqrt{\frac{1-\cos \alpha }{2}}$

$\cos \frac{\alpha }{2}=\pm \sqrt{\frac{1+\cos \alpha }{2}}$

$\cos \alpha =2{\cos }^2\frac{\alpha }{2}-1=1-2{\sin }^2\frac{\alpha }{2}$

$\tan \frac{\alpha }{2}=\pm \sqrt{\frac{1-\cos \alpha }{1+\cos \alpha }}=\frac{\sin \alpha }{1+\cos \alpha }=\frac{1-\cos \alpha }{\sin \alpha }$

$\cot \frac{\alpha }{2}=\frac{1+\cos \alpha }{\sin \alpha }=\frac{\sin \alpha }{1-\cos \alpha }$

$\sec \frac{\alpha }{2}=\frac{\pm \sqrt{\frac{\sec \alpha +1}{2\sec \alpha }}2\sec \alpha }{\sec \alpha +1}=\frac{\pm \sqrt{\frac{4{\sec }^3\alpha +{\sec }^2\alpha }{2\sec \alpha }}}{\sec \alpha +1}$

$\csc \frac{\alpha }{2}=\frac{\pm \sqrt{\frac{\sec \alpha -1}{2\sec \alpha }}2\sec \alpha }{\sec \alpha -1}=\frac{\pm \sqrt{\frac{4{\sec }^3\alpha -{\sec }^2\alpha }{2\sec \alpha }}}{\sec \alpha -1}$

---

倍角公式

$\sin 2\alpha =2\sin \alpha \cos \alpha$

$\cos 2\alpha ={\cos }^2\alpha -{\sin }^2\alpha =2{\cos }^2\alpha -1=1-2{\sin }^2\alpha$

$\tan 2\alpha =\frac{2\tan \alpha }{1-{\tan }^2\alpha }$

$\cot 2\alpha =\frac{{\cot }^2\alpha -1}{2\cot \alpha }$

$\sec 2\alpha =\frac{{\sec }^2\alpha +{\csc }^2\alpha }{{\csc }^2\alpha -{\sec }^2\alpha }=\frac{{\sec }^2\alpha {\csc }^2\alpha }{{\csc }^2\alpha -{\sec }^2\alpha }$

$\csc 2\alpha =\frac{{\sec }^2\alpha +{\csc }^2\alpha }{2\sec \alpha \csc \alpha }=\frac{{\sec }^2\alpha \csc \alpha }{2}$

---

曲率公式

$曲率K=\frac{|y^{\prime \prime }|}{{\left(1+y^{\prime 2}\right)}^{\frac{3}{2}}}$

$曲率半径\rho =\frac{1}{K}=\frac{{\left(1+y^{\prime 2}\right)}^{\frac{3}{2}}}{|y^{\prime \prime }|}$

---

点到直线距离公式

设直线 $\mathrm{L}$ 的方程为 $\mathrm{Ax}+\mathrm{By}+\mathrm{C}=0$ ，点 $\mathrm{P}$ 的坐标为 $(x0,y0)$ ，则点 $\mathrm{P}$ 到直线 $\mathrm{L}$ 的距离为: $\frac{|A{x}_0+B{y}_0+C|}{\sqrt{A^2+B^2}}$

---

常用求导公式

${\left(x^{\alpha }\right)}^{\prime }=\alpha x^{\alpha -1},{\left(a^x\right)}^{\prime }=a^x\ln a,{\left(e^x\right)}^{\prime }=e^x,{\left({\log }_{a}x\right)}^{\prime }=\frac{1}{x\ln a},(\ln x{)}^{\prime }=\frac{1}{x}$

$(\sin x{)}^{\prime }=\cos x,(\cos x{)}^{\prime }=-\sin x,(\arcsin x{)}^{\prime }=\frac{1}{\sqrt{1-x^2}},(\arccos x{)}^{\prime }=-\frac{1}{\sqrt{1-x^2}}$

$(\tan x{)}^{\prime }={\sec }^{2}x,(\cot x{)}^{\prime }=-{\csc }^{2}x,(\arctan x{)}^{\prime }=\frac{1}{1+x^2},(\mathrm{arccot}x{)}^{\prime }=-\frac{1}{1+x^2}$

$(\sec x{)}^{\prime }=\sec x\tan x,(\csc x{)}^{\prime }=-\csc x\cot x$

---

常用等价无穷小

$a^x-1\sim x\ln a$

$\arcsin (a)x\sim \sin (a)x\sim (a)x$

$\arctan (a)x\sim \tan (a)x\sim (a)x$

$\ln (1+x)\sim x$

$\sqrt{1+x}-\sqrt{1-x}\sim x$

$(1+ax{)}^b-1\sim abx$

$\sqrt[b]{1+ax}-1\sim \frac{a}{b}x$

$1-\cos x\sim \frac{x^2}{2}$

$x-\ln (1+x)\sim \frac{x^2}{2}$

$\tan x-\sin x\sim \frac{x^3}{2}$

$\tan x-x\sim \frac{x^3}{3}$

$x-\arctan x\sim \frac{x^3}{3}$

$x-\sin x\sim \frac{x^3}{6}$

$\arcsin x-x\sim \frac{x^3}{6}$

---

常用麦克劳林公式

$e^x=1+x+\frac{x^2}{2!}+\cdots +\frac{x^n}{n!}+\cdots ={\sum }_{n=0}^{\infty }\frac{x^n}{n!}$

$\sin x=x-\frac{1}{3!}{x}^3+\cdots +(-1{)}^n\frac{1}{(2n+1)!}{x}^{2n+1}+\cdots ={\sum }_{n=0}^{\infty }(-1{)}^n\frac{x^{2n+1}}{(2n+1)!}$

$\cos x=1-\frac{1}{2!}{x}^2+\cdots +(-1{)}^n\frac{1}{(2n)!}{x}^{2n}+\cdots ={\sum }_{n=0}^{\infty }(-1{)}^n\frac{x^{2n}}{(2n)!}$

$\ln (1+x)=x-\frac{1}{2}{x}^2+\cdots +(-1{)}^{n-1}\frac{x^n}{n}+\cdots ={\sum }_{n=0}^{\infty }(-1{)}^{n-1}\frac{x^n}{n},-1<x\le 1$

$\frac{1}{1-x}=1+x+x^2+\cdots +x^n+\cdots ={\sum }_{n=0}^{\infty }{x}^n,|x|<1$

$\frac{1}{1+x}=1-x+x^2-\cdots +(-1{)}^n{x}^n+\cdots ={\sum }_{n=0}^{\infty }(-1{)}^n{x}^n,|x|<1$

$(1+x{)}^{\alpha }=1+\alpha x+\frac{\alpha (\alpha -1)}{2}{x}^2+o\left(x^2\right)(x\to 0,\alpha \ne 0)$

$\tan x=x+\frac{1}{3}{x}^3+o\left(x^3\right)(x\to 0)$

$\arcsin x=x+\frac{1}{6}{x}^3+o\left(x^3\right)(x\to 0)$

$\arctan x=x-\frac{1}{3}{x}^3+o\left(x^3\right)(x\to 0)$

---

常用无穷级数

$e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\dots +\frac{x^k}{k!}+\dots (-\infty <x<\infty )$

$\ln (1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}-\cdots +\frac{(-1{)}^{k-1}{x}^k}{k}+\cdots (-1<x\le 1)$

$\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\dots +\frac{(-1{)}^{k-1}{x}^{2k-1}}{(2k-1)!}+\dots (-\infty <x<\infty )$

$\cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\dots +\frac{(-1{)}^k{x}^{2k}}{(2k)!}+\dots (-\infty <x<\infty )$

$\arcsin x=x+\frac{1}{2}\cdot \frac{x^3}{3}+\frac{1\cdot 3}{2\cdot 4}\cdot \frac{x^5}{5}+\frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}\cdot \frac{x^7}{7}\cdots +\frac{\left(\begin{array}{c}2k\\ k\end{array}\right)x^{2k+1}}{4^k(2k+1)}+\cdots (|x|<1)$

$\arccos x=\frac{\pi }{2}-\arcsin x=\frac{\pi }{2}-\left(x+\frac{1}{2}\cdot \frac{x^3}{3}+\frac{1\cdot 3}{2\cdot 4}\cdot \frac{x^5}{5}+\cdots \right)=\frac{\pi }{2}-{\sum }_{k=0}^{\infty }\frac{\left(\begin{array}{c}2k\\ k\end{array}\right)x^{2k+1}}{4^k(2k+1)}(|x|<1)$

$\arctan x=x-\frac{x^3}{3}+\frac{x^5}{5}-\cdots +\frac{(-1{)}^k{x}^{2k+1}}{2k+1}+\cdots (|x|\le 1)$

$\sinh x=x+\frac{x^3}{3!}+\frac{x^5}{5!}+\dots +\frac{x^{2k-1}}{(2k-1)!}+\dots (-\infty <x<\infty )$

$\cosh x=1+\frac{x^2}{2!}+\frac{x^4}{4!}+\dots +\frac{x^{2k}}{(2k)!}+\dots (-\infty <x<\infty )$

$\mathrm{arcsinh}x=x-\left(\frac{1}{2}\right)\frac{x^3}{3}+\left(\frac{1\cdot 3}{2\cdot 4}\right)\frac{x^5}{5}-\left(\frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}\right)\frac{x^7}{7}+\cdots +\left(\frac{(-1{)}^k(2k)!}{2^{2k}k{!}^2}\right)\cdot \frac{x^{2k+1}}{2k+1}+\cdots (|x|<1)$

$\mathrm{arctanh}x=x+\frac{x^3}{3}+\frac{x^5}{5}+\cdots +\frac{x^{2k+1}}{2k+1}+\cdots (|x|<1)$

---

基本积分表

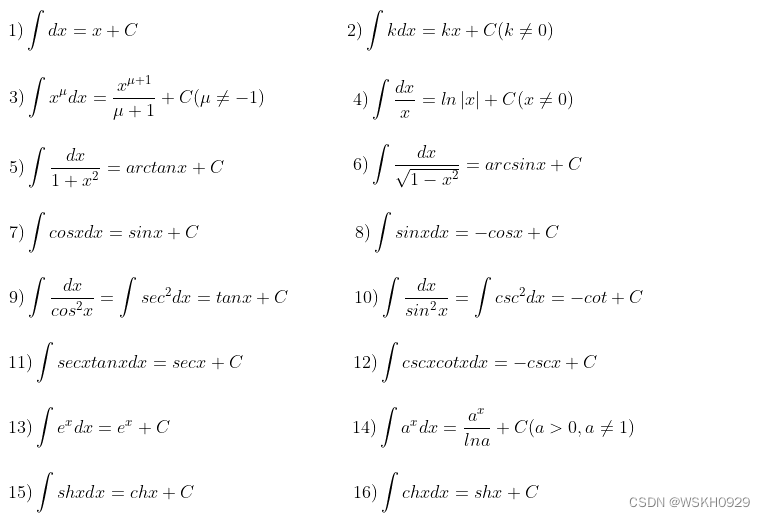
基本积分表的扩充

---