PS: 代码涉及的随机函数和一些容器虽然是C++的, 但算法是通用的, 这些容器java等其它语言里也都能找到类似的存在.

1. 最朴素暴力的做法.

void cal1()
{
	int i = 0, j = 0, num = 0;
	int result[M];

	result[0] = rand() % N;	//第一个肯定不重复, 直接加进去

	for (i = 1; i < M; i++)	//获得剩下的(M-1)个随机数
	{
		num = rand() % N;	//生成0 ~ N之间的随机数字

		for (j = 0; j < i; j++) 
		{
			if (num == result[j]) //如果和result数组中某个元素重复了
			{
				i--;	//重新开始此次循环
				break;
			}
		}

		if (j == i) // 说明新产生的数和数组里原有的元素都不同, 则add进去
		{
			result[i] = num;
		}
	}
}

2. 在方法1的基础上我们可以进行优化. 每轮遍历n太耗时, 那么优化成logn如何, 于是采用一下set作为辅助, 为了利用它logn的时间复杂度. 代价是多了一个M大小的set的空间.

void cal2()
{
	set<int> s;
	int num = 0, index = 0;
	int result[M];

	while (index < M)
	{
		num = rand() % N;
		if (s.find(num) == s.end())	//如果没找到
		{
			s.insert(num);
			result[index++] = num;
		}
	}
}

3. 如果你被方法1和2无穷的重复比较弄烦了, 可能想到, 每次新产生的随机数都要和已有的数去进行比较是否已存在, 越往后这种方法的效率越低, 不停在做无用功. 那么反其道而行如何? 几斤几两咱们都亮在牌面上, OK, 把所有数先都列出来, 从里面往外筛选, 那么每次选出来的, 肯定是不重复的. 只需要选M次就可以了.

void cal3()
{
	int result[M] = {0};
	deque<int> deq;	//队列
	int i = 0, index;

　　	for (i = 0; i < N; i++) //初始化, 把所有N个数都放到容器里, 从这里面往外挑, 每次必不重复
	{
		deq.push_back(i);
	}

	for (i = 0; i < M; i++)	//挑选出M个数
	{
		index = rand() % deq.size(); //注意deq.size()是不断变小的, 但是每次都符合随机特性
		result[i] = deq.at(index);	//把deq数组index位置的元素赋给result[i]
		deq.erase(deq.begin() + index);	//从deq队列中把该元素删除
	}
}

4. 方法3是思路比较理想化和直接, 实际操作中, 你会发现比方法1都要慢很多很多, 原因就出在容器的erase函数, 内部实现的本质是内存片的拷贝, 这个操作相当相当的耗时.这个和语言无关, 换成java等其它语言, 类似的这种函数都是同样的原理. 其实思考到方法3, 真理已经呼之欲出了. 我们沿着这个思路继续优化算法. 从中剔除元素的想法是好的, 但是方法不佳. 其实我们需要的本来就是基本的数组就可以了, 速度还快, 用deque, vector这些容器无非是为了使用他们的erase函数把某个数剔除出去不参与下次的随机过程. 随着一个个数被选出, 容器的大小也在不停变小, 其实使用数组, 利用下标的偏移, 我们直接就可以做到了! 和用数组实现一个队列或者栈不是一样的吗, 无非就是数组下标的移动! 于是沿着方法3的思想, 我们每次随机出来一个下标index(0 <= index < size(size初值为N)), 每次把arr[index]这个位置的元素甩到数组最后面就可以了, 就相当于剔除操作了!

void cal4()
{
	int result[M] = {0};
	int data[N] = {0};
	int i = 0, index = 0;

	for (i = 0; i < N; i++)	//初始化
	{
		data[i] = i;
	}

	for (i = 0; i < M; i++)
	{
		index = rand() % (N - i);
		result[i] = data[index];	//把data数组index位置的元素赋给result[i]
		data[index] = data[N - i - 1];	//从data数组末尾(这个位置在不停前移)拿一个数替换到该位置, 相当于这个元素被剔除了
	}
}

算法都写出来了, 贴一下实际测试的时间数据, 增加一下直观感受.

(注: 下面数据在vs2008平台下测试, 用的GetTickCount()函数, 这个函数精度在10~16ms范围内. 由于机器配置不同, 下面数据仅供参考, 只为表达一种直观上的时间差异)

N = 1,000, M = 1,000 : (可以看出, N值较小时, 方法1甚至优于方法2, 因为这时logn相对于n的速度优势并不明显, 却多了set的处理开销, 方法3最慢)

N = 10,000, M = 10,000 : (方法2的logn优势已经显现, 方法3的龟速放大的很明显)

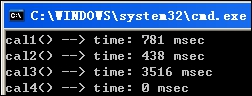
N = 30,000, M = 30,000 : (方法2较之1的优势更加明显, 方法3依然最耗时)

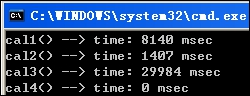
N = 50,000, M = 50,000 : (方法1和2已经算不出结果了, 方法1下班没关机, 执行了一宿第二天还是没出结果, 方法2等了15分钟也没结果, 虽然会比1会快点, 原理是一样的, 就是越到后面随机出不重复数的几率越小了, 做太多无用功. 方法3虽然慢, 还是出的来结果的, 方法4依然坚挺, 0ms!)

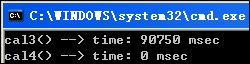
N = 100,000, M = 100,000: (十万, 依旧是0)

N = 1,000,000, M = 1,000,000: (1百万, GetTickCount()函数有10~16ms的误差, 从下面1千万和1亿的时间来看, 这个算法是绝对线性的, 因此此时实际时间应该在23ms左右. 当然, 这时开始已经换成了堆数组)

N = 10,000,000, M = 10,000,000: (1千万)

N = 100,000,000, M = 100,000,000: (1亿, 将近100M的内存啦, 十亿的时候编译器不支持了)

总结: 无论从代码的实现来看, 还是实际的效率来看, 方法4都是当之无愧的佼佼者. 当然, 文中所测都是在M和N相等的情况, 这种测试用例数量级越大, 对于方法1和2来说越是艰难. 算法是死的, 实际情况是多变的, 实际应用中我们灵活选择甚至混合使用这些方法, 比如N非常大, M相对N来说却又比较小(比如N=1亿, M=1万), 这时候方法1也是完全可以接受的, 毕竟方法1比较省空间, 而方法4是用空间换了时间. 可以说M和N越趋近, 方法4的多余空间开销是越值得的, 否则也可能会有得不偿失的情况呀. 

鉴于此, 又一种思路浮现出来, 可以再继续演化一下, 用于M比较大但是仍远小于N的情况. 

5. 我们把方法4的data数组去掉, 但是想象中是有这么个数组的. 初始时这个数组里的值都等于其下标. 循环的过程中, 如果某个坐标index被随机到了, 那么把这个记录加到map里, key为index, 从数组尾部拿来一个元素作为value. 

void cal5()
{
	map<int, int> m;
	int result[M] = {0};
	int index = 0;

	for (int i = 0; i < M; i++)
	{
		index = rand() % (N - i);

		if (m.find(index) == m.end())	//如果没找到, 说明该坐标第一次被随机到, 该位置的值没有被改过, 值和坐标相等
		{
			result[i] = index;
		}
		else	//如果该位置的值被改过, 那么值在m[index]是这个位置的值
		{
			result[i] = m[index];
		}

		//更新这个index对应的值, 和方法同样道理, 用数组后面的数替代该位置的值
		//这个地方比方法复杂点, 需要多个判断, 因为N-i-1位置的值的情况不同
		if (m.find(N - i - 1) == m.end())	//如果map里没有N-i-1这个key
		{
			m[index] = N - i - 1;
		} 
		else
		{
			m[index] = m[N - i - 1];
		}
	}
}

测试结果如下:

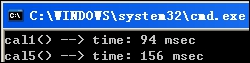
M = N = 100,000的时候仍然1秒多就可以出结果, 当然, 这种算法是应用于M远小于N的情况, M,N都是十万的时候有这个结果还是不错的:

这是N = 10,000,000, M = 10,000时的结果, 可见纯数组操作还是更快些, 虽然有很多轮无用功.

N = 10,000,000, M = 100,000时, 方法1就已经无响应了, 而方法5的优点则显而易见了, 这个速度还是可以接受的. 

可见, N越大, M和N越接近, 方法1越无力, 反之方法1甚至是个不错的方法, 速度快, 省空间. 所以还是那句话, 算法是死的, 而实际情况是复杂的, 但是我们可以把死的算法进行灵活运用.没有最好只有最适合的, 一切取舍依实际情况吧! : )

全文完. 

版权所有, 转载请标明出处.   http://blog.csdn.net/aa2650/article/details/12507817