Logit模型和Logistic模型
一、离散选择模型(Discrete Choice Model, DCM)常见的DCM模型:二项Logit(Binary Logit)、多项Logit(Multi-nominal Logit)、广义Logit(Generalized Logit)、条件Logit(Conditional Logit)、层式Logit(Nested Logit)、有序Logit/Probit(Ordered Logit
一、离散选择模型(Discrete Choice Model, DCM)
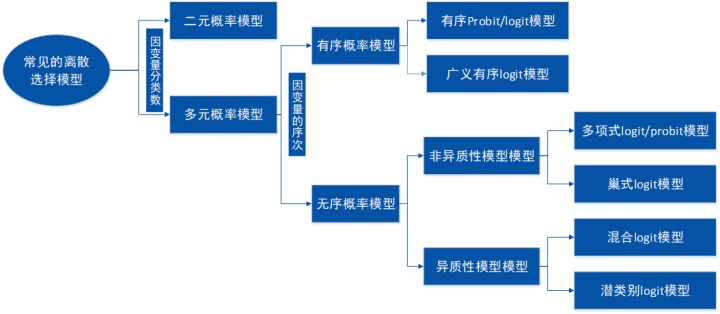
| 常见的DCM模型:二项Logit(Binary Logit)、多项Logit(Multi-nominal Logit)、广义Logit(Generalized Logit)、条件Logit(Conditional Logit)、层式Logit(Nested Logit)、有序Logit/Probit(Ordered Logit/Probit)、混合Logit(Mixed Logit)等 |
| 拟合离散选择模型的软件:SAS、NLOGIT、Stata、Python、R、Matlab等 |
| Daniel McFadden丹尼尔·麦克法登:在离散选择模型研究方面的贡献而被授予2000年的诺贝尔经济学奖 |
| 线性回归模型是分析相关关系最常用模型,因变量为离散时进行拟合时会违背线性回归模型的一些假设条件, 区别主要在于:
|
1.1用途
离散选择行为即因变量不是一个连续的变量:(品牌选择、定性影响因素分析(天气条件等)、出行方式选择)
1.2基本要素
一个基本的选择过程(Choice Process)包含一下4个要素:
1.2.1:决策者(Decision Maker)即做出选择行为的主体
| 决策者自身的属性会对选择的结果产生影响 |
| 调查、研究用户/消费者的选择行为时需要收集受访者的个人社会经济状况的资料 |
| 年龄、性别、收入、工作类型 |
1.2.2:备选方案集(Alternatives)通常会有多个方案供决策者选择(出行方式选择:飞机或高
铁)
| 通用方案集(Universal Choice Set) |
| 可行方案集(Feasible Choice Set) |
| 实际考虑的方案集(Consideration Choice Set) |
1.2.3:各个方案的属性(Attributes of Alternatives)备选方案自身属性中影响决策者的因素称之为一个属性(Attributes),通常会建立指标体系
| 不同的方案属性描述了各个方案在不同的维度上可以提供给人们的效用(Utility) |
| “效用最大化”是最为常见的决策准则 |
| 方案在不同属性上的差异,决策者提供一个选择的空间 |
1.2.4:决策准则(Decision Rules)不同的决策者在做出方案选择时的行为准则存在差异。
| 优势准则 (Dominance Rule) | 不同维度上分别存在优势难以选择 |
| 下限准则 (Satisfactory Rule) | 利用“下限准则”进行决策时可能最终会产生多个选择结果 |
| 多重排序准则 (Lexicographic Rule) | 属性按重要程度从高到低进行排列,不断循环删选 |
| 效用最大化准则 (Utility Maximization Rule) | 不同属性建立权重(每个方案属性类别、权属性重一样,属性值不同) |
1.3离散选择模型的类型
选择是可以根据需要,符合条件即可
| 备选方案的数量 | 二项选择模型(Binomial choice models) | 备选方案只有两个选项:是、否 |
| 多项选择模型(Multinomial choice models) | 备选方案数量为3个或3个以上 | |
| 备选方案的特征 | 无序离散选择模型(Unordered DCM) | 存在等级程度 能见度:极好、好、一般、较差 |
| 有序离散选择模型(Ordered DCM) | 无等级程度 |
1.4随机效用变量 ε
| Probit模型 | 随机效用变量 ε 服从正态分布 |
| Logit模型 | 随机效用变量 ε 服从Logistic分布 |
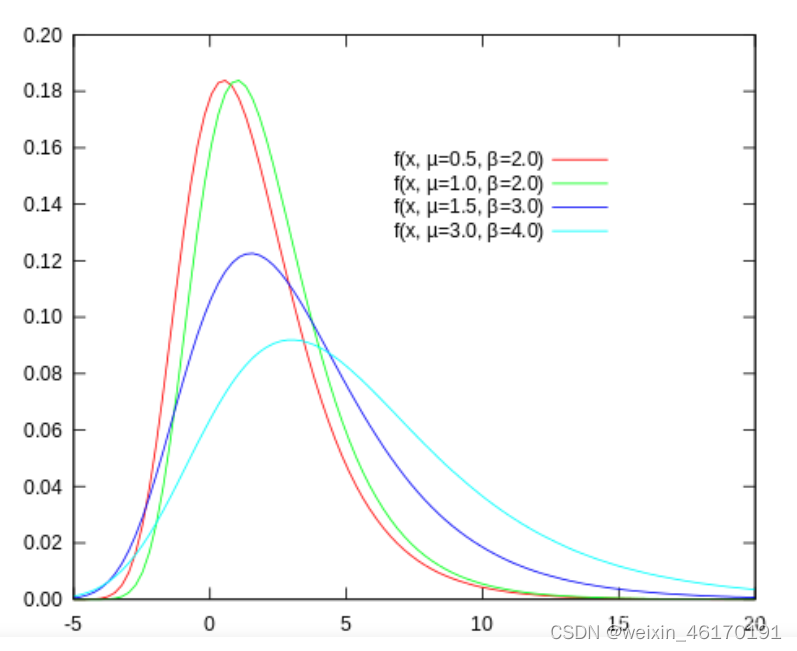
| 二项Logit模型 | 服从Gumbel分布 |

1.5数据计量尺度
| Nominal Scale分类数据 (名义尺度、名义数据、定类数据等) |
|
| Ordinal Scale,定序数据 (顺序尺度、序列数据、等级数据等) |
|
| Interval Scale,定距数据 (间隔尺度、定距尺度、等距数据等) |
|
| Ratio Scale,定比数据 (比例尺度、比例数据、等比数据等) |
|
Multi-nominal Logit——多类别Logit模型
Ordered Logit——有序Logit模型
二项Logit(Binary Logit)——Bi-nomial Distribution模型
二、Logit模型
2.1,关于概率
| 概率(Probability) | p(A)=A事件发生的次数/所有事情发生的次数 | 掷骰子为例。掷出点数为6的概率为1/6 | p(A)在0-1之间 |
| 几率、可能性、胜率(Odds) | Odds=A事件发生的次数/非A事件发生的次数 | 掷骰子为例。掷出点数为6的Odds为1/5 | Odds理论下假设甲乙二人掷骰子对赌;若甲出1块钱赌掷到6点,乙需要投注5块钱才能保证公平。 |
| Odds和概率(P)之间关系 | Odds=p/(1-p) Odds=A事件发生的概率/非A事件发生的概率 | 概率等于0.5的时候,Odds等于1 | |
| 优势比Odds Ratio | 相对优势的概念 | ||
2.2,Logit理解
| Logit =Odds的对数 | logit=log(it)=log(odds) =log(p/(1-p)) | |
| 对Odds取自然对数(,就可以将概率P从范围(0,1)映射到 | ||
| 取对数后函数没有上下限,符合回归模型的假设,可以采用线性回归建模 | ||
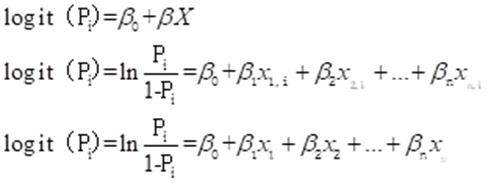 | ||
| Logit 模型的回归系数 如果 | ||
2.3、二项Logit模型(Binary Logit)
| 基于基于效用最大化准则:决策者 n 选择方案 i 和 j ,对应的效用为Ui和Uj,如果 即决策者n选择i的概率等价于
| |
| 影响决策的是方案之间效用的相对差值 | |
| 二项Logit模型中,决策者 n 选择方案 i 的概率可以表示为 | 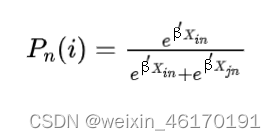 |
| 随机效用变量 ε 服从Gumbel分布 | Gumbel分布是一种极值型分布,常被用于极端事件的估计和预测,如地震、洪水等极端自然灾害现象的预测 |
| Gumbel分布不是对称的,其分布呈现一定的偏态 | |
| 如果随机变量 εin 和εjn 均服从Gumbel分布,且 εin 与εjn 之间相互独立,则 εin-εjn 服从Logistic分布
| |
2.4,多项Logit模型, Multi-nominal Logit,MNL
| 基于基于效用最大化准则:决策者 n 有k个选择方案,对应的效用为 即决策者n选择i的概率等价于 记为: 注:此时为一组不等式,表示K组比较同时发生的概率 | |
| 注意事件之间相互独立:即为多项Logit模型的IIA特性,Independent of Irrelevant Alternative, | |
| 用X表示决策主体n的相关属性: 多项Logit模型常见形式
|
| IIA特性:无关方案的独立性:随机项的i.i.d( independent identically distributied,独立同分布) | |
| 在MNL模型中 任意两个方案被选中的概率之比只和方案本身的属性有关,属性效用分为明确部分+随机部分 假定所有方案的随机项 | 由于随机项中经常包含未观测到的指标 常常导致随机项之间并不独立,存在一定关联 典型案例“红/蓝公交悖论” |
| IIA假设作为强假设,实际方案中效用往往随机项并不独立,利用MNL模型导致与实际存在偏差 | |
| hausman specification test:豪斯曼检验 比较所有样本基础上获得的参数估计值与剔除所选方案的样本后得到的参数估计值:没有显著差别,则通过假设,IIA假设成立 没有通过,需要使用其他模型(嵌入式logit,混合logit) | |
| 数据处理 | |
| 个人属性——决策者个人属性 | 性别、收入、工作类型等 |
| 方案属性—每个方案的属性 | 例如出行方案中每个交通工具对应的费用、时间、舒适性、安全性等 |
当因变量Y有多个选择是,可以利用多项Logit模型进行建模,多想logit模型包含一系列模型
Ordered Logit Model——有序Logit模型
Generalized Logit Model——广义logit模型
Conditional Logit Model——条件Logit模型
2.4.1 有序Logit模型Ordered Logit Model
如果因变量Y是由序的,则称为有序Logit模型
例如:因变量杯子大小:小杯、中杯、大杯,销售分析哪些因素影响顾客选择,由于杯子是有序递增的,可以考虑使用有序Logit模型
2.4.2 广义logit模型 Generalized Logit Model
如果自变量X全部都和决策者相关的属性,不包含任何方案相关的属性,则采用广义logit模型
例如:因变量不同的冰激凌味道,自变量是受访者年龄、受访者玩电子游戏的得分,受访者玩拼图游戏得分,全部与决策主体相关的信息。
| 决策主体n一共有J个方案,
决策者n选择方案J的概率为
|
| 共有J组系数, 个人属性每增加1个单位,对方案的影响程度不一样,例如第一个属性增加1,对方案1的影响值为 |
| 在Generalized Logit Model中,个人属性对每个方案的影响程度是不一样的 |
2.4.3 条件Logit模型Conditional Logit Model
如果自变量X全部都和方案相关的属性,不包含任何和决策者相关的属性,则采用条件Logit模型
例如:交通出行方案,知道了每个出行者选择各种交通方式的费用、时间、舒适度、安全性等数据,但不知道出行者自身相关的信息。
|
决策者n选择方案J的概率为
|
| 只有一组系数,任意一个方案属性增加或者减少一个单位,对每个方案的影响程度是一样的 |
| 方案属性对每个方案的影响程度是相同的 |
2.5 混合logit模型
数据即有决策者信息、方案的相关属性,采用参数是一种分布的logit模型(即系数不是一个常数,而是一个随机分布)
5.mixed conditional logit models
2.4 嵌入式logit(Nested Logit )
参考:
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容


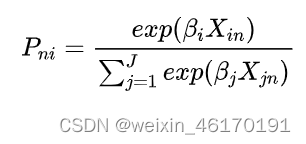






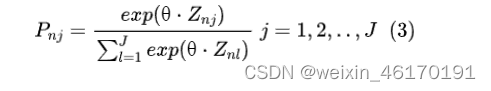







所有评论(0)