目录

一、什么是并查集

二、并查集的存储结构

三、并查集的基本操作

（一）初始化

（二）Find操作

（三）Union操作

四、并查集的优化

（一）Union操作优化（小树并入大树）

（二）Find操作优化（压缩路径）

---

一、什么是并查集

        并查集的逻辑结构是一个包含N个元素的集合，如图：

        我们将各个元素划分为若干个互不相交的子集，如图：

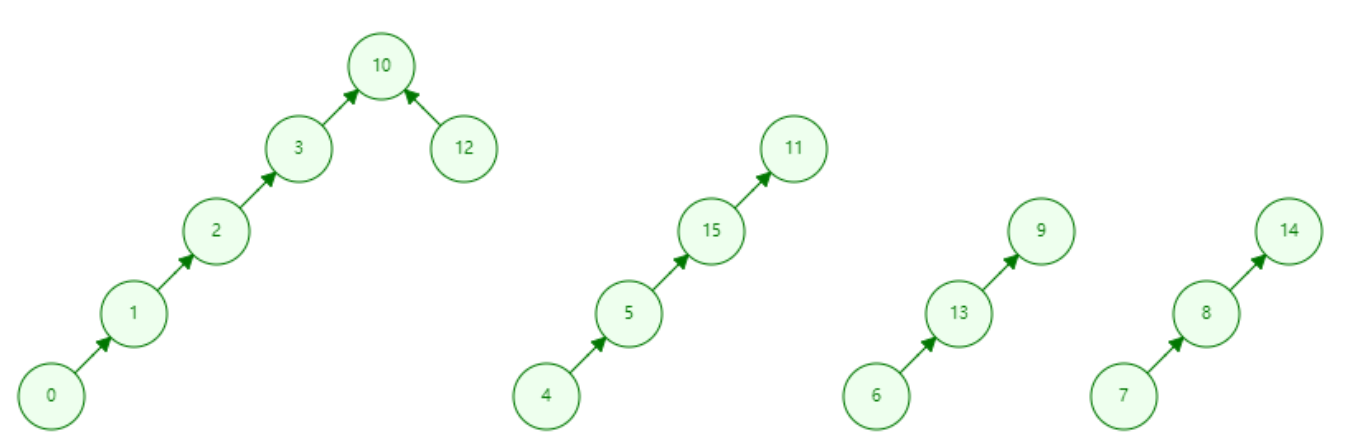
        我们假设第一个集合中的元素为：苹果、橘子、香蕉等各种水果，结点10就表示水果1。
        我们假设第二个集合中的元素为：油菜、香菜，芹菜等各种蔬菜，结点11就表示蔬菜。
        我们假设第三个集合中的元素为：高数、线代、计网等各种学科，结点9就表示学科。
        我们假设第四个集合中的元素为：蓝莓、草莓、杨梅等各种水果，结点14就表示水果2。
        （注：四个集合互不相交）

        

        下面有几个问题：

1. 如何判断高数（结点6）是什么集合门类下的？
   从结点6向上找（6 -> 13 -> 9）,结点9代表学科门类。
2. 如何判断苹果（结点0）和橘子（结点12）是否属于同一集合？
   从结点0开始向上找（0 -> 1 -> 2 -> 3 -> 10）
   从结点12开始向上找（12 -> 10）
   所以，它两属于同一个集合
3. 集合一中的水果要与集合四中的水果合成一组，这时应该怎么做？
   我们可以理解为结点10带领的是水果（1）大家族，结点14带领的是水果（2）大家族，只要结点10与结点14合并到一起，便可以实现两个集合的合并，其余结点不需要操作，如图：
   

        在一些有N个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中，其特点是看似并不复杂，但数据量极大，若用正常的数据结构来描述的话，往往在空间上过大，计算机无法承受;即使在空间上勉强通过，运行的时间复杂度也极高，只能用并查集来描述。

二、并查集的存储结构

        并查集的存储结构可以通过 树的双亲表示法 来理解。

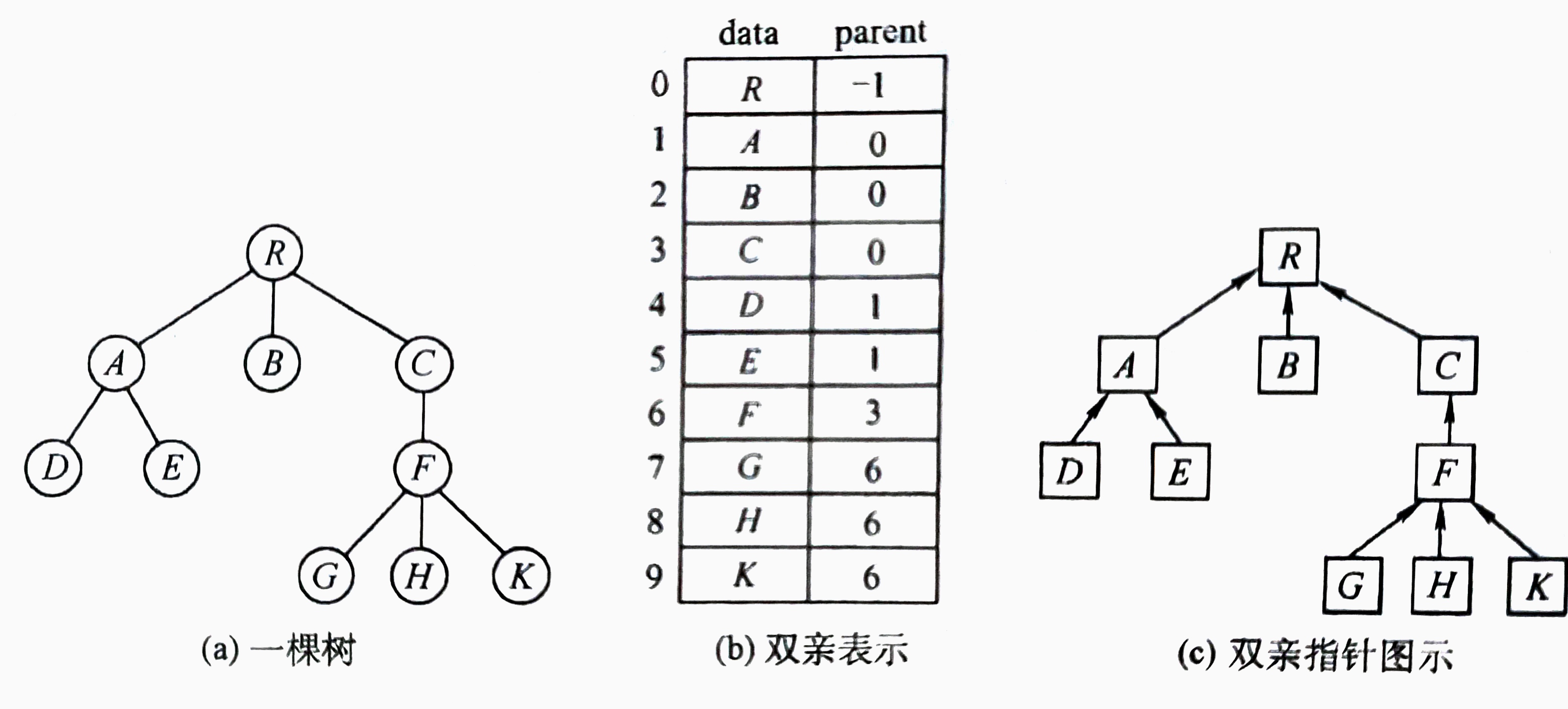
        我们先来看一下树的双亲表示法：

这种存储方式采用一组连续空间来存储每个结点，同时在每个结点中增设一个伪指针，指示其双亲结点在数组中的位置。如图所示，根结点下标为0，其伪指针域为-1。          该存储结构利用了每个结点（根结点除外）只有唯一双亲的性质，可以很快得到每个结点的双亲结点，但求结点的孩子时需要遍历整个结构。

        接下来，我们来看并查集：

        若设有一个全集合为 S ={0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}，初始化时每个元素自成一个单元素子集合，每个子集合的数组值为 -1，如图：

         经过一段时间的计算，这些子集合合并为3个更大的子集合，并查集的树形表示和存储结构如图：

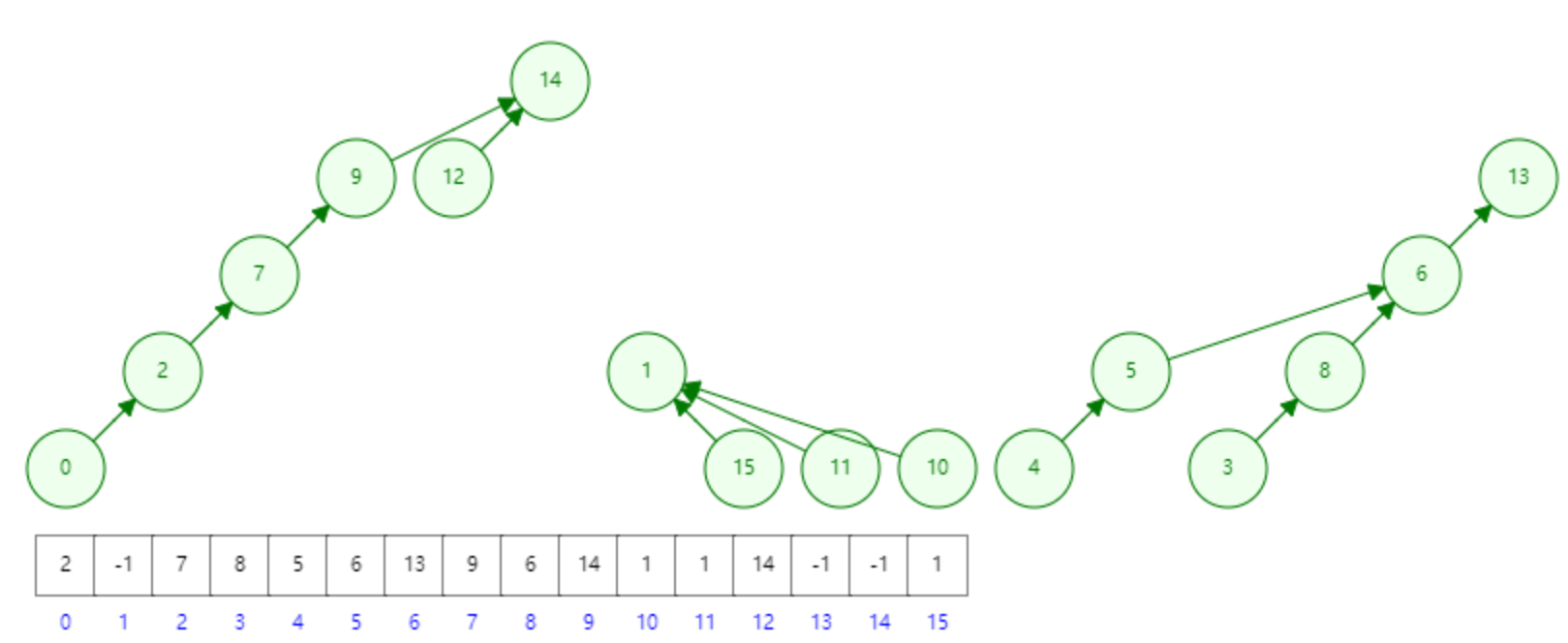
         可见，并查集可用数组进行表示，数组下标序号表示该数据元素，数组值存放其双亲信息。

分析： 对于上一个图 结点 0 的数组值为 2 ，代表双亲是 2 ； 结点 2 的数组值为 7 ，代表双亲是 7 ； 结点 7 的数组值为 9 ，代表双亲是 9 ； 结点 9 的数组值为 14 ，代表双亲是 14 ； 结点 14 的数组值为 -1 ，代表该结点为根结点 ； 至此，我们仅通过数组这一数据结构便完成了结点信息的存放和结点双亲的查找。

   下面，我们用代码描述并查集：

• 并查集的结构定义为：

  #define SIZE 100
  int UFSets[SIZE]; //集合元素数组

三、并查集的基本操作

（一）初始化

• 并查集的初始化即使每个元素自成一个单元素子集合，每个子集合的数组值为-1

  void Initial(int S[])
  {
  	for (int i = 0; i < SIZE; i++)
  		S[i] = -1;
  }

（二）Find操作

• 查找操作即在并查集S中查找并返回包含元素 x 的树的根

  int Find(int S[], int x)
  {
  	while (S[x] >= 0) //循环寻找 x 的根
  		x = S[x];
  	return x; //根的 S[] 小于0
  }

（三）Union操作

• 合并操作即将两个子集合的根合并到一起

  void Union(int S[], int Root1, int Root2)
  {
  	//要求Root1与Root2是不同的，且表示子集合的名字
  	if (Root1 == Root2) return;
  	S[Root2] = Root1;
  }

  （Root2的双亲指向了Root1，意味着Root2带领的整个集合都指向了双亲Root1,实现了合并）

四、并查集的优化

（一）Union操作优化（小树并入大树）

• 问题：若只有一个子集合，且这一个子集合是一条细长的链，若结点数是 n ,那么查找的最坏时间复杂度是O(n)
• 优化思路：在每次Union操作构建树的时候，尽可能让树不长高
• 方法：
  1. 每个根结点不再用-1表示，用根结点的绝对值表示树的结点总数，例如，原先数组值如图

  

  图中表示结点 1 、13 、14是根结点。
  优化后为

  

  图中仍然表示结点 1、13、14为根结点，同时说明了根结点1子集合下共有4个元素，其他同理。
  2.Union操作，让小树合并到大树
  代码编写

  void Union(int S[], int Root1, int Root2)
  {
  	//要求Root1与Root2是不同的，且表示子集合的名字
  	if (Root1 == Root2) return;
  	if (S[Root2] > S[Root1]) //Root2结点数更少
  	{
  		S[Root1] += S[Root2];
  		S[Root2] = Root1; //小树合并到大树，即Root2指向Root1
  	}
  	else
  	{
  		S[Root2] += S[Root1];
  		S[Root1] = Root2;
  	}
  }

•  结果：Union操作优化后，Find操作的最坏时间复杂度变为了

（二）Find操作优化（压缩路径）

• 问题：反复查找某个结点的根结点，每次都会花费大量时间
• 优化思路：只要查找一次，就将查找路径上的所有结点都挂到根结点下面，如图,查找L的根结点A，查找一次过后，就将E、B、L全部挂到根结点A之下
  
•  方法：
  代码编写

  int Find(int S[], int x)
  {
  	int root = x;
  	while (S[root] >= 0) root = S[root]; //循环找到根
  	while (x != root) //x不为根结点，则压缩路径
  	{
  		int t = S[x]; //t指向x的父节点
  		S[x] = root; //x直接挂到根结点下
  		x = t;
  	}
  	return root; //返回根节点编号
  }

•  结果：Find操作优化后，Find操作的最坏时间复杂度为，是一个增长很缓慢的函数，通常<=4