Hybrd A(混合A)算法

2010年，斯坦福Dmitri Dolgov, Sebastian Thrun, Michael Montemerlo等人在国际顶级期刊International Journal of Robotics Reaserch上首次提出一种满足车辆运动学的算法(Hybrid A*),并在(DARPA)的城市挑战赛中得以运用。Hybrid A*算法是一种图搜索算法，改进于A*算法。与普通的A*算法区别在于，Hybrid A*规划的路径考虑了车辆的运动学约束，即满足了车辆的最大曲率约束。Hybrid A*算法的启发式包括两种: non-holonomic without-obstacles和holonomic with obstacles。前者考虑了车辆的运动约束，但不考虑障碍物，一般使用RS曲线，Dubins曲线；后者将车辆当成网格地图上面的点，但考虑了障碍物。

Dubins曲线

Dubins曲线是在满足曲率约束和规定的始端和末端的切线方向的条件下，连接两个二维平面（即X-Y平面）的最短路径，并假设车辆行驶的道路只能向前行进。在1957年, Lester Eli Dubins (1920–2010) 证明任何路径都可以由最大曲率弧或直线段组成（两点之间的路径必须存在）。换句话说，连接两点的最短路径将通过最大曲率的圆弧和直线段的构成。

车辆单车模型

Simple Car模型是一个表达车辆运动的简易模型。Simple Car模型将车辆看做平面上的刚体运动，刚体的原点位于车辆后轮的中心；x轴沿着车辆主轴方向，与车辆运动方向相同；车辆在任意一个时刻的姿态可以表述为 $(x,y,\theta )$ ，车辆的运动速度为 $v$ ， $L$ 为前轴到后轴的长度， $\delta _{f}$ 为最大前轮转角，对应的转弯半径为 $R$ 。有 $R=L/\tan (\delta _{f})$

运动学方程：

$\dot{x} = vcos(\theta )$

$\dot{y} = vsin(\theta )$

$\dot{\theta} = \omega =\frac{v}{R}$

其中， $\theta$ 为偏航角，有了运动学方程，给定时间间隔 $T_{s}$ 和 $v$ 就可以得到一系列的点，也就是路径了，且是满足运动学要求的，而点的疏密，则可以由 $T_{s}$ 和 $v$ 来确定，令 $\delta =vT_{s}$ ：

$x{_{new}}=x_{prev}+\delta *cos(\theta )$

$y{_{new}}=y_{prev}+\delta *sin(\theta )$

$\theta _{new}=\theta _{prev}+\frac{\delta }{R}$

Dubins曲线计算

令S为车辆直行的Motion Primitive，L和R分别为车辆左转和右转的Motion Primitive，可以证明，任意起点到终点的Dubins最短路径可以由不超过三个Motion Primitives构成。由三个Motion Primitives构成的序列称为一个Word。由于两个连续的、相同的Motion Primitive可以合并为一个Motion Primitive，因此所有可能的Word有10中组合，Dubins证明最优的Word组合只能是6种组合之一。如下图，分别是LSL，RSR，RSL，LSR，RLR，LRL（注意：对于RLR和LRL两种情况，那个大圆的半径是与两个小圆的半径相等的，否则采用其他4种情况更优)

前四种的计算原理可以视为一种情况，后两种可以视为一种情况，详细的计算过程参考最后的参考链接，这里我们只给出代码用到的计算结果。

设起始点为 $s(x_{i},y_{i},\alpha _{i})$ ，终点为 $g(x_{g},y_{g},\beta _{g})$ ，为方便计算，将起点设定为坐标原点，起始点到终点连线方向 $\theta$ 为x轴方向。经过坐标转换，起始点坐标为 $s(0,0,\alpha )$ ，终点坐标为 $g(d,0,\beta )$ ，其中：

$\theta =atan2(\frac{y_{g}-y_{i}}{x_{g}-x_{i}})$

$D=sqrt((x_{i}-x_{g})^{2}+(y_{i}-y_{g})^{2})$

$d=D/R$

$\alpha =mod(\alpha _{i}-\theta ,2\pi )$

$\beta =mod(\beta _{g}-\theta ,2\pi )$

上面将D除上R是为了正则化R，这样每个最小转弯半径都为1，由角度计算弧长时更方便，弧长即等于角度的弧度。

对于前四种情况，设车辆在起始圆上走过的长度为 $t$ ，直线长度为 $p$ ，第二个圆上的圆弧长度为 $q$ ，如图所示LSL情况：

LSL情况

构建方程组：

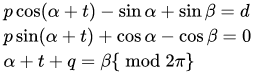
求解：

总长度为：

RSR情况

构建方程组：

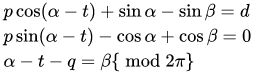
求解：

RSL情况

构建方程组：

求解：

LSR情况

构建方程组

求解：

对于后两种情况，一定是 $D<4R$ ，否则会有之前的情况最优。如图所示，LRL 情况时构成的三个圆，都是等半径的，也即等于 1.

LRL情况

构建方程组：

求解：

总长度为：

RLR情况

构建方程组：

求解：

Reeds-Shepp曲线

相比于Dubins曲线只允许车辆向前运动，Reeds Shepp曲线运动模型既允许车辆向前运动，也允许车辆向后运动。J Reeds和L Shepp证明Reeds Shepp Car从起点 $q_{I}$ 到终点 $q_{G}$ 的最短路径一定是下面的word的其中之一。word中的"|"表示车辆运动朝向由正向转为反向或者由反向转为正向。

每个world都由 $L^{+}$ ， $L^{-}$ ， $R^{+}$ ， $R^{-}$ ， $S^{+}$ ， $S^{-}$ 这六种primitives组成，其中， $L^{+}$ 表示车辆左转前进； $L^{-}$ 表示车辆左转后退； $R^{+}$ 表示车辆右转前进； $R^{-}$ 表示车辆右转后退， $S^{+}$ 表示车辆直行前进； $S^{-}$ 表示车辆直行后退。 $C_{\beta }$ 表示两个曲线长度一样的曲线部分， $C_{\pi /2}$ 表示曲线部分有90度。

Reeds and Shepp曲线的word所有组合不超过48种，所有的组合一一枚举如下：

位置姿态统一化

一般在计算之前，会将车辆的姿态归一化。假设车辆的初始姿态为 $q_{I}=(x_{1},y_{1},\theta _{1})$ ，目标姿态为 $q_{G}=(x_{2},y_{2},\theta _{2})$ ，车辆的半径为 $r=\rho$ 。归一化的过程就是向量的平移和旋转的过程，使得变换后的起始位姿 $q_{I}=(0,0,0)$ ，目标姿态为 $q_{G}=(x,y,\phi )$ ，车辆的转弯半径r=1。其中，

$x=((x_{2}-x_{1})*cos(\theta _{1})+(y_{2}-y_{1})*sin(\theta _{1}))/\rho$

$y=(-(x_{2}-x_{1})*sin(\theta _{1})+(y_{2}-y_{1})*cos(\theta _{1}))/\rho$

$\phi =\theta _{2}-\theta _{1}$

代码如下:

double x1 = s1->getX(), y1 = s1->getY(), th1 = s1->getYaw();
double x2 = s2->getX(), y2 = s2->getY(), th2 = s2->getYaw();
double dx = x2 - x1, dy = y2 - y1, c = cos(th1), s = sin(th1);
double x = c * dx + s * dy, y = -s * dx + c * dy, phi = th2 - th1;

return reedsShepp(x / rho_, y / rho_, phi)

利用对称关系降低求解复杂度

Reeds shepp曲线有48种组合，编程时一一编码计算比较麻烦，因此可以利用其对称性降低求解工作量。具体原理为，将目标点变更后，相当于原目标点A关于y轴与x轴进行对称，得到新的目标点B，生成一组新的路径 $t$ ， $u$ ， $v$ 。

timefilp对称性（符号对称性）

符号对称性指的是 $+-$ 对称性，假设我们推导出从起始姿态 $q_{I}(x_{1},y_{1},\theta _{1})$ 到达目标姿态的路径计算方法， $path=calcPath(x_{1},y_{1},\theta _{1},x_{2},y_{2},\theta _{2})$ ， $L^{+}S^{+}R^{+}$ 类型轨迹。利用对称性，将目标pose修改为 $(-x_{2},y_{2},-\theta _{2})$ ，带入同样的Path计算函数： $path=calcPath(x_{1},y_{1},\theta _{1},-x_{2},y_{2},-\theta _{2})$ 就得到从 $(x_{1},y_{1},\theta _{1})$ 到 $(x_{2},y_{2},\theta _{2})$ 的 $L^{-}S^{-}R^{-}$ 类型的运动路径。

reflect对称性（RL对称性）

RL对称性指的是R与L的互换，不涉及符号，将目标姿态修改为 $(x_{2},-y_{2},-\theta _{2})$ ，带入同样的Path计算函数： $path=calcPath(x_{1},y_{1},\theta _{1},x_{2},-y_{2},-\theta _{2})$ 就得到从 $(x_{1},y_{1},\theta _{1})$ 到 $(x_{2},y_{2},\theta _{2})$ 的 $R^{+}S^{+}L^{+}$ 类型的运动路径。

timeflip+reflect

结合timeflip对称性和reflect对称性，将目标姿态修改为 $(-x_{2},-y_{2},\theta _{2})$ ，带入同样的Path计算函数： $path=calcPath(x_{1},y_{1},\theta _{1},-x_{2},-y_{2},\theta _{2})$ 就得到从 $(x_{1},y_{1},\theta _{1})$ 到 $(x_{2},y_{2},\theta _{2})$ 的 $R^{-}S^{-}L^{-}$ 类型的运动路径。

对应关系如下表：

$(x,y,\theta )$	$(-x,y,-\theta )$	$(-x,-y,\theta )$	$(x,-y,-\theta )$
$L^{+}$	$L^{-}$	$R^{-}$	$R^{+}$
$R^{+}$	$R^{-}$	$L^{-}$	$L^{+}$
$S^{+}$	$S^{-}$	$S^{-}$	$S^{+}$
$L^{-}$	$L^{+}$	$R^{+}$	$R^{-}$
$R^{-}$	$R^{+}$	$L^{+}$	$L^{-}$
$S^{-}$	$S^{+}$	$S^{+}$	$S^{-}$

Reeds-Shepp曲线结算流程图

维诺（Voronoi）地图

在路径规划中，地图是最基本的要素，也是反映现实世界的一种重要的表达。在常用的地图中，距离地图、栅格地图和维诺地图等。其中，栅格地图是地图分成一个个边长相等的栅格来表示环境信息。距离地图是在规划算法进行搜索过程中提供扩展节点到障碍物的最近距离。其中，最近距离是通过欧式距离所计算得到。维诺地图是一种对距离地图的扩展。通过距离地图和广义泰森多边形(generalized Voronoi diagram，GVD)相结合所形成。

Voronoi图的定义

又叫泰森多边形或Dirichlet图，它是由一组由连接两邻点直线的垂直平分线组成的连续多边形组成。如图所示：

Voronoi图的特点

（1）每个V多边形内有一个生成元；

（2）每个V多边形内点到该生成元距离短于到其它生成元距离；

（3）多边形边界上的点到生成此边界的生成元距离相等；

（4）邻接图形的Voronoi多边形界线以原邻接界线作为子集。

混合A*算法中的使用

在Hybrid A*算法中，通过使用维诺地图获得扩展节点的势能值，并将其作为启发函数的部分代价值添加到代价函数中，使用这样的方式让扩展节点与障碍物形成一定的距离。

势能的计算公式为：

$\rho _{v}(x,y)=\left\{\begin{matrix} (\frac{\alpha }{\alpha +d_{0}(x,y)})(\frac{d_{v}(x,y)}{d_{0}(x,y)+d_{v}(x,y)})(\frac{d_{0}-d_{max}}{d_{max}})^{2} & d_{0}\leqslant d_{0}^{max}\\ 0 &other \end{matrix}\right.$

其中，

$\rho _{v}(x,y)$ ：节点(x,y)处的势能，取值从0到1，当 $d_{0}>d_{0}^{max}$ 时，(x,y)势能为0，势能值到达最大的时候是(x,y)在障碍物上或者里面，势能值到达最小的时候是(x,y)在广义泰森多边形的边上。

$d_{0}$ ：是节点到达最近障碍物的距离；

$d_{v}$ ：是节点到达维诺地图边的最近距离；

$\alpha$ ：表示势能下降速率，为常数， $\alpha \epsilon [0,+\infty )$ ，当 $\alpha$ 值越大，(x,y)处的势能下降的越慢；

$d_{0}^{max}$ ：势能的控制范围，为常数；

A*算法

A*(A star)算法最初发表于1968年，由Stanford研究院的Peter Hart, Nils Nilsson以及Bertram Raphael发表。它可以被认为是Dijkstra算法的扩展。是一种很常用的路径查找和图形遍历算法。它有较好的性能和准确度。

如图，A*算法从起始点到达目标点，过程描述如下：

1. 把起点加入 open list（开启列表或开放列表）。

2. 重复如下过程：

a. 遍历 open list ，查找 F 值最小的节点，把它作为当前要处理的节点。

b. 把这个节点移到 close list（关闭列表或封闭列表）。

c. 对当前节点相邻的每个节点？

◆ 如果它是不可抵达的或者它在 close list 中，忽略它。否则，做如下操作。

◆ 如果它不在 open list 中，把它加入 open list ，并且把当前节点设置为它的父节点，记录该节点的 F ， G 和 H 值。

◆ 如果它已经在 open list 中，检查这条路径 ( 即经由当前节点到达该节点 ) 是否更好，用 G 值作参考。更小的 G 值表示这是更好的路径。如果是这样，把它的父亲设置为当前节点，并重新计算它的 G 和 F 值。如果你的 open list 是按 F 值排序的话，改变后你可能需要重新排序。

d. 停止，当你

◆ 把终点加入到了 open list 中，此时路径已经找到了，或者

◆ 查找终点失败，并且 open list 是空的，此时没有路径。

3. 保存路径。从终点开始，每个方格沿着父节点移动直至起点，这就是你的路径。

* 初始化open_set和close_set；
* 将起点加入open_set中，并设置优先级为0（优先级最高）；
* 如果open_set不为空，则从open_set中选取优先级最高的节点n：
    * 如果节点n为终点，则：
        * 从终点开始逐步追踪parent节点，一直达到起点；
        * 返回找到的结果路径，算法结束；
    * 如果节点n不是终点，则：
        * 将节点n从open_set中删除，并加入close_set中；
        * 遍历节点n所有的邻近节点：
            * 如果邻近节点m在close_set中，则：
                * 跳过，选取下一个邻近节点
            * 如果邻近节点m也不在open_set中，则：
                * 设置节点m的parent为节点n
                * 计算节点m的优先级
                * 将节点m加入open_set中

A*算法通过代价值F来确定节点的优先级，F的值越小，则节点的优先级越高。

$F(n)=G(n)+H(n)$

其中 $G(n)$ 表示由起点到节点n的实际消耗，又被称作耗散函数。 $H(n)$ 表示节点n到终点的估计消耗，又被称作启发函数。H的计算方式有很多种，比如曼哈顿H(n) = x + y，或者欧几里得式H(n) = sqrt(x^2 + y^2)等。启发函数对于A*算法的搜索效率是至关重要的，而研究合理的、有效的启发来估计扩展节点到目标点的代价至关重要。

Hybrid A*算法

Hybrid A和A区别

	Hybrid A*	A*
维数	$(x,y,\theta ,R)$	$(x,y)$
H(n)	max(Reeds-Shepp，A*)	Manhattan/Euclidean
扩展节点	符合车辆运动学模型的节点	二维平面坐标点
节点与节点连接处	交点可以不是栅格顶点	交点是栅格顶点
缺点	不具有完备性	不满足车辆运动学特

Hybrid A*算法描述

Hybrid A*算法是标准A*算法的一种改进，通过这种方式能够使得A*算法满足车辆运动学。与A*算法类似，先将起始点加入开启列表中。在将开启列表中优先级最高的节点加入到关闭列表中前，判断当前节点是否小于阈值（源码中为15米），如果小于阈值，则用Reed-Shepp曲线或Dubins曲线与目标相连接，并加入车身轮廓判断是否与障碍物碰撞。如果和障碍物无碰撞，则保留该曲线并生成路径。如果与障碍物发生碰撞则放弃该曲线，并从开启列表中重新寻找节点，重新进行扩展。

A*算法的扩展节点是栅格的交点，因此不能解决在连续空间内车辆朝向和位置的问题。而Hybrid A*算法通过使用车辆运动学生成的轨迹替代A*算法中的节点，从而解决路径不满足车辆运动学的问题。如图所示，A*算法扩展节点时为八个格子，Hybrid A*算法扩展节点时有六个运动基原，向前扩展三个运动模式，向后扩展三个运动模式。

在Hybrid A*算法中将启发函数分成两种：无障碍物的非完整性约束启发代价和有障碍物的完整性启发式代价。

无障碍物的非完整约束启发代价

这第一个启发式代价主要是忽略了在路径规划中障碍物对规划器的影响。这项启发函数必须获得车辆的最小转弯半径作为输入。并且，改启发函数主要是通过离散周围的栅格地图，获得不同方向坐标点并使用最优曲线计算路径长度。比如，在需要计算起始点到目标点 $(x_{g},y_{g},\theta _{g})$ 的最优曲线的路径长度时。首先，是在起始点 $(x_{i},y_{i},\theta _{i})$ 使用Dubins曲线或者Reeds-Shepp曲线连接目标点 $(x_{g},y_{g},\theta _{g})$ ，得到最优曲线的路径长度。然后，计算最优曲线的距离，并作为启发函数的代价值 $H_{1}(n)$ 。因为这项代价函数忽略了环境中障碍物的影响，所以可以通过离线的形式计算出来。同时，这项代价函数的主要目的是为修剪A*搜索树的分支，避免了到达目标点时，所规划路径方向与目标方向不一致的问题。

有障碍物的完整性启发式代价

第二项代价函数主要是考虑环境中障碍物信息，但忽略了车辆的最小转弯半径对其的影响。通过在每个节点上使用Djikstra算法获得该节点到达目标点的最近距离作为其代价函数的代价值 $H_{2}(n)$ 。由于Djikstra算法能够在类似迷宫环境中获得扩展节点到目标点的最近路径，因此可以避免在扩展过程中Hybrid A*算法扩展朝向不正确的问题。