观察vector.push_back()具体拷贝机制

实验需要条件

1. vector容器
2. 创建一个能通过拷贝控制函数打印相关信息的类，这里我自己写了一个简易的String类来打印信息

实验代码：

	vector<String> vec;

	String s = "1";
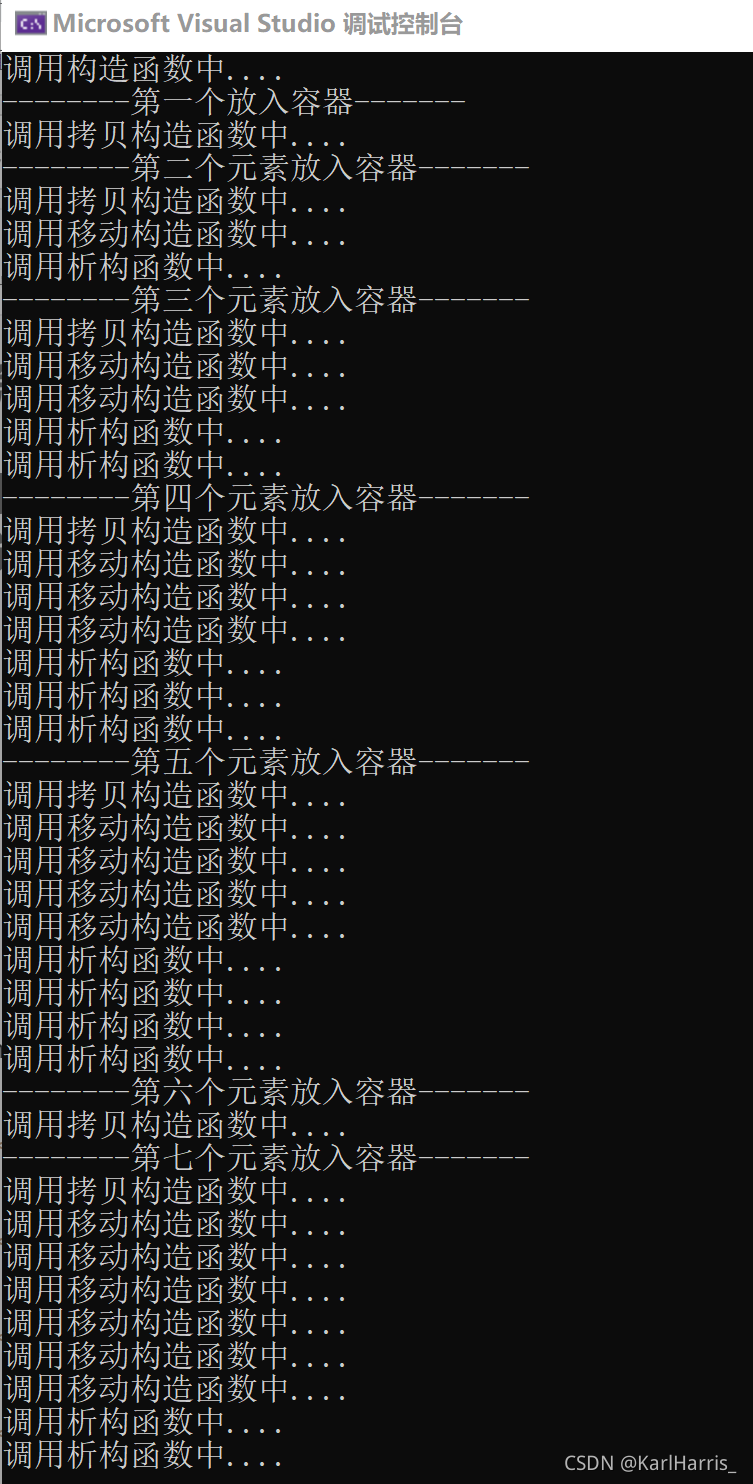
	cout << "--------第一个放入容器-------" << endl;
	vec.push_back(s);
	cout << "--------第二个元素放入容器-------" << endl;
	vec.push_back(s);
	cout << "--------第三个元素放入容器-------" << endl;
	vec.push_back(s);
	cout << "--------第四个元素放入容器-------" << endl;
	vec.push_back(s);
	cout << "--------第五个元素放入容器-------" << endl;
	vec.push_back(s);
	cout << "--------第六个元素放入容器-------" << endl;
	vec.push_back(s);
	cout << "--------第七个元素放入容器-------" << endl;
	vec.push_back(s);
	cout << "--------第八个元素放入容器-------" << endl;
	vec.push_back(s);
	cout << "--------第九个元素放入容器-------" << endl;
	vec.push_back(s);
	cout << "--------第十个元素放入容器-------" << endl;
	vec.push_back(s);
	cout << "--------放入完毕-------" << endl;

实验结果：

分析实验结果

看到实验结果一开始是头皮发麻的，其实通过查找规律，可以验证侯杰老师在深入理解STL源码中所说的vector容器大小1.5倍增长

步骤1

vec.push_back(s);

实验结果：

实验结果很显然符合我们的预期，调用push_back函数时，拷贝一次s,此时vector容器大小为1

步骤2

vec.push_back(s);
vec.push_back(s);

实验结果：

这时候结果开始令人费解了，我们预期应该调用两次拷贝构造函数，为什么这里出现了一次移动构造函数与一次析构函数，没关系，这时候我们先记住此时容器大小为2就行，继续下一步

步骤3

vec.push_back(s);
vec.push_back(s);
vec.push_back(s);

实验结果：

第三次push_back不出我们所料，令人费解的出现了两次移动构造函数与两次析构函数
此时容器大小为3

步骤4

vec.push_back(s);
vec.push_back(s);
vec.push_back(s);
vec.push_back(s);

实验结果：

此时容器大小为4

步骤5

vec.push_back(s);
vec.push_back(s);
vec.push_back(s);
vec.push_back(s);
vec.push_back(s);

实验结果：

此时容器大小为5
完蛋了，都已经push_back五个元素了，还是令人费解，难道要寄了吗？！最后一次push_back，还不出现转机直接不干了！

步骤6

vec.push_back(s);
vec.push_back(s);
vec.push_back(s);
vec.push_back(s);
vec.push_back(s);
vec.push_back(s);

实验结果：

我的天啊，当我们push_back第六个元素的时候出现不一样的结果了，开心！这时候居然只出现了一次拷贝构造函数，此时容器大小是6

步骤7

vec.push_back(s);
vec.push_back(s);
vec.push_back(s);
vec.push_back(s);
vec.push_back(s);
vec.push_back(s);
vec.push_back(s);

实验结果：

该死，第七次又出现了奇奇怪怪的移动构造函数与析构函数
此时容器大小为7

步骤8&9

vec.push_back(s);
vec.push_back(s);
vec.push_back(s);
vec.push_back(s);
vec.push_back(s);
vec.push_back(s);
vec.push_back(s);
vec.push_back(s);
vec.push_back(s);

第八和第九次都只构造了一次，此时容器大小为9

步骤10

vec.push_back(s);
vec.push_back(s);
vec.push_back(s);
vec.push_back(s);
vec.push_back(s);
vec.push_back(s);
vec.push_back(s);
vec.push_back(s);
vec.push_back(s);
vec.push_back(s);

结果我就不放了，第十次依然是出现了奇怪的移动构造函数与析构函数
此时容器大小为10
这个时候我回想起之前侯杰老师所讲的vector容器1.5倍增长的结论，心中的疑惑解除了
在这里我们要搞清vec.size()与vec.capacity()的区别

vec.size()	vec.capacity()
容器目前容纳的元素个数	容器最大容纳元素个数

而且满足vec.size()<=vec.capacity()
一旦vec.size()>vec.capacity()vec会重新分配一块更大的空间，并且容量为之前容量的1.5倍，这就是所谓的1.5倍增长。然而，开辟了新的空间，我们需要把旧空间的元素拷贝到新空间去，但由于旧元素被拷贝后就不会再用了，此时我们可以使用移动构造函数让新空间窃取旧空间的元素权限，以减少拷贝所带来的时间开销，同时，旧空间需要被摧毁。
上面的这段操作不就和步骤2、3、4、5、7、10所伴随的奇奇怪怪的移动构造函数与析构函数很相似吗，为了描述方便，我将这段操作简述为出现增长

所谓的1.5倍增长指的是vector的最大容纳元素个数！
通过结论，我们可以模拟一下vector增长的过程
这里初始时vector容器大小为1
最大容纳元素个数增长过程：
1 -> 2 -> 3 -> 4 -> 6 -> 9

我们可以模拟一下push_back时候vec的最大容量capacity，就会发现秘密了！

步骤2：出现增长
此时capacity为1，size为1，push_back后size=2>capacity=1，需要重新分配空间，并且出现将旧空间的1个元素移动到新空间，析构旧空间的1个元素，符合实验结果调用一次移动构造函数与一次析构函数

步骤3：出现增长
此时capacity为2，size为2，push_back后size=3>capacity=2，需要重新分配空间，并且出现将旧空间的2个元素移动到新空间，析构旧空间的2个元素，符合实验结果调用两次移动构造函数与两次析构函数

步骤4：出现增长
此时capacity为3，size为3，push_back后size=4>capacity=3，需要重新分配空间，并且出现将旧空间的3个元素移动到新空间，析构旧空间的3个元素，符合实验结果调用三次移动构造函数与三次析构函数

步骤5：出现增长
此时capacity为4，size为4，push_back后size=5>capacity=4，需要重新分配空间，并且出现将旧空间的4个元素移动到新空间，析构旧空间的4个元素，符合实验结果调用四次移动构造函数与四次析构函数

步骤6：
此时capacity为6，size为5，push_back后size=6=capacity=6，不需要重新分配空间，因为最大容纳空间还足以满足分配元素的需求

步骤7：出现增长
此时capacity为6，size为6，push_back后size=7>=capacity=6，需要重新分配空间，并且出现将旧空间的6个元素移动到新空间，析构旧空间的6个元素，符合实验结果调用六次移动构造函数与六次析构函数

步骤8：
此时capacity为9，size为7，push_back后size=8<capacity=9，不需要重新分配空间，因为最大容纳空间还足以满足分配元素的需求

步骤9：
此时capacity为9，size为8，push_back后size=9=capacity=9，不需要重新分配空间，因为最大容纳空间还足以满足分配元素的需求

步骤10：出现增长
此时capacity为9，size为9，push_back后size=10>capacity=9，需要重新分配空间，并且出现将旧空间的9个元素移动到新空间，析构旧空间的9个元素，符合实验结果调用九次移动构造函数与九次析构函数

步骤11：通过实验结果我们可以预测步骤11不会出现增长
此时capacity为13，size为10，push_back后size=11<capacity=13

实验结论：

原来啊，步骤2、步骤3、步骤4、步骤5、步骤7、步骤10出现奇奇怪怪的移动与析构函数是因为push_back元素的时候发生了size>capacity，此时需要将最大容纳空间向1.5倍扩充，以满足增加元素的需求!至于步骤1、步骤6、步骤8、步骤9因为满足size<=capacity，所以可以直接在旧空间上增加元素，而不需要重新分配一段1.5倍率的内存空间