模式识别|机器学习学期总结
文章目录一、主成分分析 PCA二、奇异值分解 SVD三、K均值聚类四、均值漂移聚类五、EM算法六、SOM算法七、朴素贝叶斯算法八、逻辑斯蒂回归九、支持向量机 SVM十、决策树10.1 ID3算法10.2 C4.5算法10.3 决策树剪枝10.4 CART10.4.1 回归树10.4.2 分类树10.4.3 CART剪枝一、主成分分析 PCA利用正交变换把原来的数据转换为低维度的线性无关的数据几何上
文章目录
一、主成分分析 PCA
利用正交变换把原来的数据转换为低维度的线性无关的数据
几何上理解就是旋转坐标系,然后将数据映射到新坐标系,让映射到新坐标系的数据方差尽量大,从而最大程度地保留了原来数据信息。
二、奇异值分解 SVD
奇异值分解是一种矩阵因子分解方法。假设A是m*n的矩阵,那么有如下的分解:
A = U Σ V T A=U\Sigma V^T A=UΣVT
其中 U,V分别是m,n阶的正交矩阵, Σ \Sigma Σ是由降序排列的非负的对角线元素组成的m*n对角矩阵。
三、K均值聚类
K-means 聚类,主要思想步骤:
- 随机选取K个指定类的中心点
- 进行聚类:计算所有点到这K个点的距离,每个点被指派到与其最近的中心点的类中
- 计算新的类中心:计算新的类中各个样本的均值点,作为新的中心点
- 重复2直到收敛
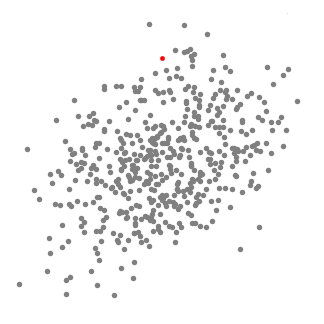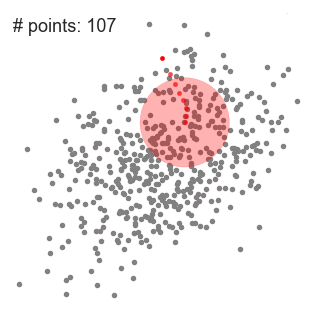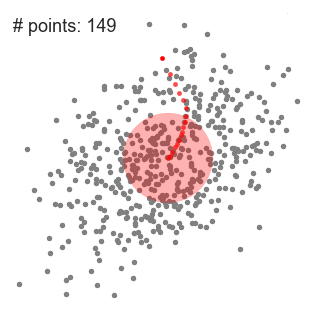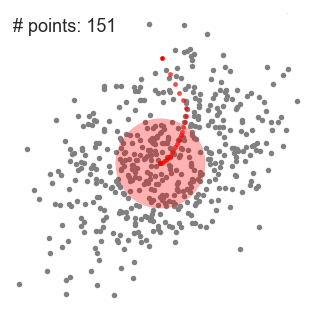
四、均值漂移聚类
不要指定K,即类的个数
思想:沿着密度上升的方向进行聚类,一个类聚合收敛后随机选择新的一点进行聚类,直到所有点都被遍历,按点的遍历次数指派类。

五、EM算法
用于含有隐变量的概率模型参数的极大似然估计,其中用到了琴生不等式来放缩。
不明白
六、SOM算法
自组织映射神经网络(SOM)
不明白
有监督算法
七、朴素贝叶斯算法
思想:后验概率可以根据先验概率计算;条件独立性假设。
其中,先验概率可以由极大似然估计来计算。

有N个样本,其中k个标签是yi,那么P(yi)就可以估计为 k/N
P ( x j ∣ y i ) = P ( x j , y i ) P ( y i ) P(x_j|y_i)=\frac{P(x_j,y_i)}{P(y_i)} P(xj∣yi)=P(yi)P(xj,yi)
八、逻辑斯蒂回归
思想:用极大似然估计一个概率模型。
P ( Y = 1 ∣ X ) = e x p ( w ⋅ x + b ) 1 + e x p ( w ⋅ x + b ) P(Y=1|X) = \frac{exp(w \cdot x +b)}{1+exp(w \cdot x +b)} P(Y=1∣X)=1+exp(w⋅x+b)exp(w⋅x+b)
P ( Y = 0 ∣ X ) = 1 1 + e x p ( w ⋅ x + b ) P(Y=0|X) = \frac{1}{1+exp(w \cdot x + b)} P(Y=0∣X)=1+exp(w⋅x+b)1
就是求解以上模型的w和b。
给定训练集合 T = { ( x 1 , y 1 ) , . . . , ( x N , y N ) } T=\{(x_1,y_1),...,(x_N,y_N)\} T={(x1,y1),...,(xN,yN)}
并且设 P ( Y = 1 ∣ x ) = π ( x ) , P ( Y = 0 ∣ x ) = 1 − π ( x ) P(Y=1|x)=\pi(x), \quad P(Y=0|x)=1-\pi(x) P(Y=1∣x)=π(x),P(Y=0∣x)=1−π(x)
那么似然函数为 ∏ i = 1 N [ π ( x i ) ] y i [ 1 − π ( x i ) ] 1 − y i \prod_{i=1}^N[\pi(x_i)]^{y_i}[1-\pi(x_i)]^{1-y_i} ∏i=1N[π(xi)]yi[1−π(xi)]1−yi
对这个函数取对数然后求极大值,就估计出了w和b
九、支持向量机 SVM
思想:在一堆数据点中寻找一个超平面wx+b=0,使得间隔最大化。也就是估计参数w和b。
直观: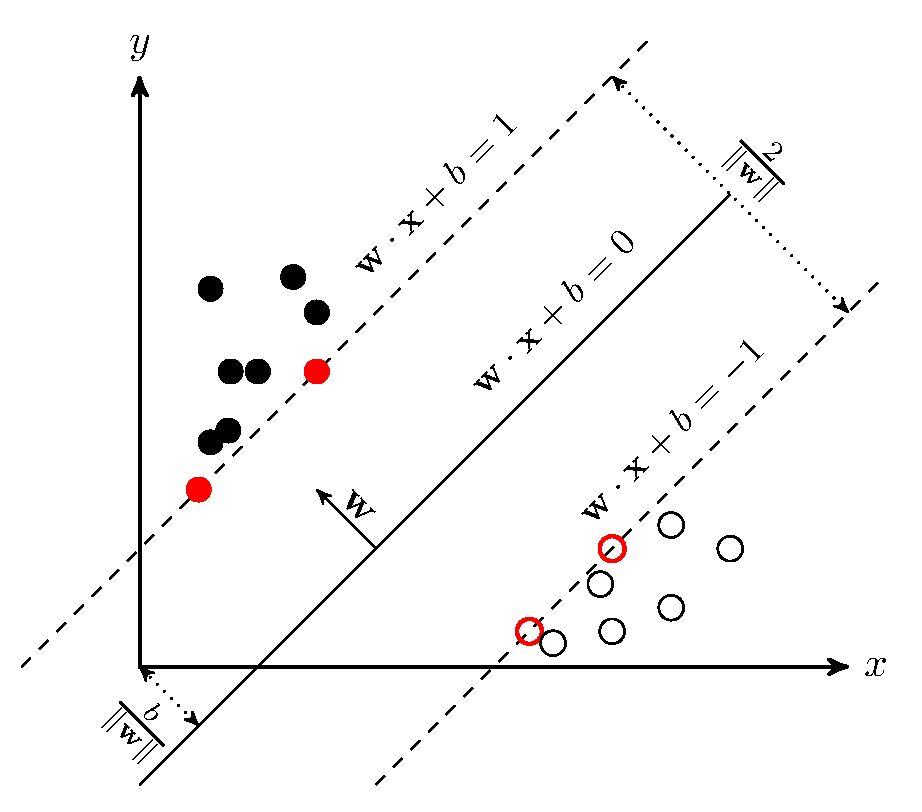
线性可分支持向量机、线性支持向量机、非线性支持向量机。
核函数。
序列最小优化算法。
SVM的数学推导较多。核函数用到拉格朗日对偶定理。
十、决策树
信息熵: 
其中 C k C_k Ck 表示集合 D 中属于第 k 类样本的样本子集。
条件熵:

其中 D i D_i Di 表示 D 中特征 A 取第 i 个值的样本子集, D i k D_{ik} Dik 表示 D i D_i Di 中属于第 k 类的样本子集。
信息增益:信息熵减去条件熵
信息增益越大表示使用特征 A 来划分所获得的“纯度提升越大”。
10.1 ID3算法
ID3 算法的核心思想就是以信息增益来度量特征选择,选择信息增益最大的特征进行分裂。算法采用自顶向下的贪婪搜索遍历可能的决策树空间。
10.2 C4.5算法
C4.5利用信息增益比来选择特征。
信息增益比:(信息熵-条件熵)/特征熵

其中 n 是特征A取值个数
比如说规模特征,有大、中、小 共三个取值
10.3 决策树剪枝
决策树可能过拟合,因此需要剪枝
10.3.1 预剪枝
在节点划分前来确定是否继续增长,及早停止增长的主要方法有:
- 节点内数据样本低于某一阈值;
- 所有节点特征都已分裂;
- 节点划分前准确率比划分后准确率高。
预剪枝不仅可以降低过拟合的风险而且还可以减少训练时间,但另一方面它是基于“贪心”策略,会带来欠拟合风险。
10.3.2 后剪枝
在已经生成的决策树上进行剪枝,从而得到简化版的剪枝决策树。
C4.5 采用的悲观剪枝方法,用递归的方式从低往上针对每一个非叶子节点,评估用一个最佳叶子节点去代替这课子树是否有益。如果剪枝后与剪枝前相比其错误率是保持或者下降,则这棵子树就可以被替换掉。C4.5 通过训练数据集上的错误分类数量来估算未知样本上的错误率。
后剪枝决策树的欠拟合风险很小,泛化性能往往优于预剪枝决策树。但同时其训练时间会大的多。
10.4 CART
分类与回归树(classfication and regression tree,CART)
CART假设决策树是二叉树,内部节点特征取值为“是”和“否”,左分支为“是”,右分支为“否”。递归构建二叉决策树,对回归树用平方误差最小化准则,对分类树用基尼指数最小化准则,进行特征选择,生成二叉树。
10.4.1 回归树
此时数据是连续的,采用平方误差最小的原则来选择特征。

其中,A为划分特征,s为划分点,D1为小于s的数据点,D2为大于s的数据点。
10.4.2 分类树
基尼指数:
建树思想:对每一个特征A以及它的每一个可能取值a,计算A=a的基尼指数。在所有特征以及取值中,选择基尼指数最小的特征与取值作为最优特征与最优切分点,生成两个子结点。
10.4.3 CART剪枝
不明白
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容








所有评论(0)