【实验目的】

对模式识别有一个初步的理解，能够根据自己的设计对贝叶斯决策理论算法有一个深刻地认识，理解二类分类器的设计原理。

【实验原理】

最小风险贝叶斯决策可按下列步骤进行：

【实验内容】

类条件概率的曲线：

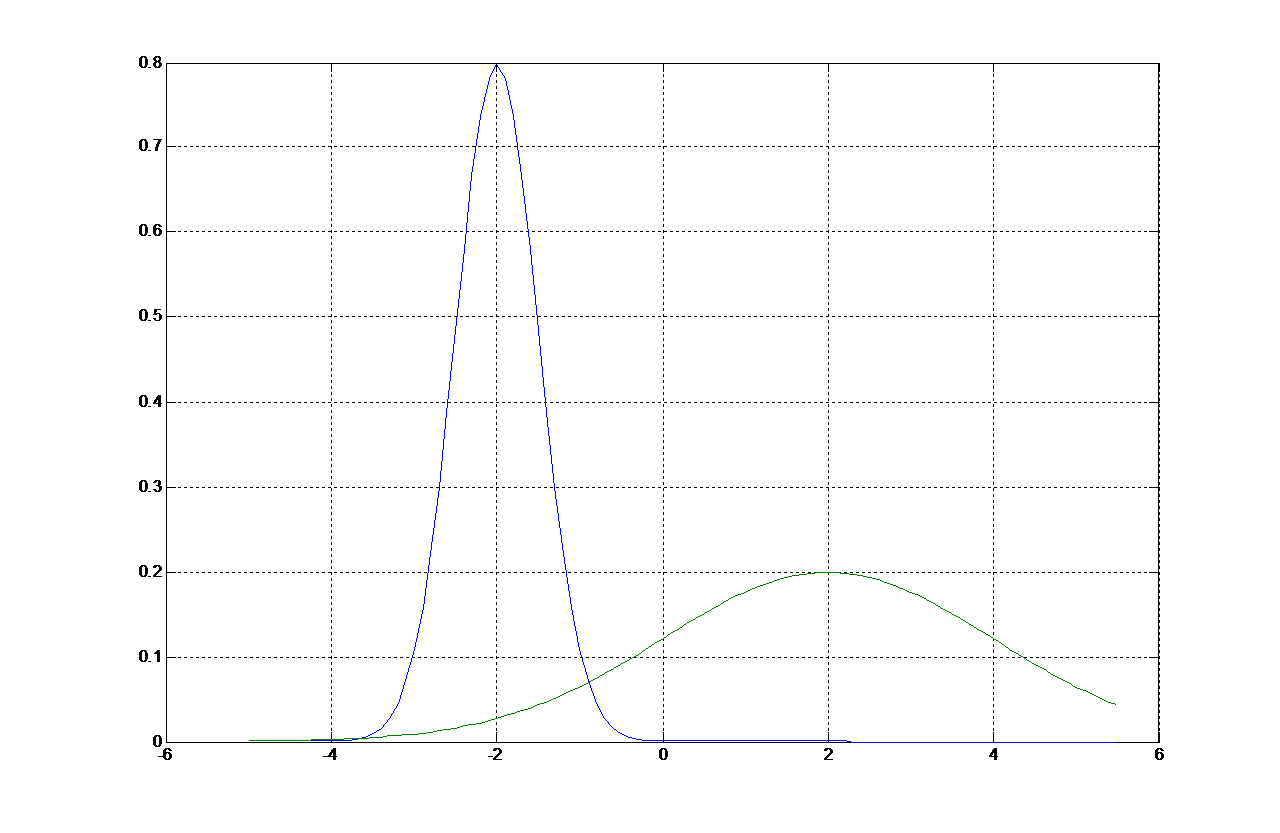
【实验要求】

1) 用python完成基于最小错误率的贝叶斯分类器的设计，要求程序相应语句有说明文字，要求有子程序的调用过程。

2) 根据例子画出后验概率的分布曲线以及分类的结果示意图。

3) 如果是最小风险贝叶斯决策，决策表如下：

最小风险贝叶斯决策表：

请重新设计程序，完成基于最小风险的贝叶斯分类器，画出相应的条件风险的分布曲线和分类结果,并比较两个结果。

最小错误实验程序：

import numpy as np
import math
import matplotlib.pyplot as plt

x = [-4.9847, -3.5649, -2.2401, -0.9780, -0.8032, -2.9531,
     -2.8605, -3.9287, -3.3414, -2.2792, -3.6549,-3.0852,
     -4.1934, 2.9792, -0.9980, 0.8932, 1.1982, 3.2682,
     -1.5899, -1.4985, -0.7531, -0.4321, -1.2186, 4.3532]
y = range(24)
P_w1 = 0.92  # 先验概率1
P_w2 = 0.08  # 先验概率2

mean1 = -2  #均值1
std1 = np.sqrt(0.25)  #方差1
mean2 = 2   #均值2
std2 = np.sqrt(4)  #方差2

data_w1 = []  # 正常细胞
data_w2 = []  # 非正常细胞
x1 = 0
x2 = 0
for x_i in x:

    P_x_w1 = 1 / (std1 * pow(2 * math.pi, 0.5)) * np.exp(-((x_i - mean1) ** 2) / (2 * std1 ** 2))  # 条件概率密度函数1
    P_x_w2 = 1 / (std2 * pow(2 * math.pi, 0.5)) * np.exp(-((x_i - mean2) ** 2) / (2 * std2 ** 2))  # 条件概率密度函数2

    P_x = P_x_w1 * P_w1 + P_x_w2 * P_w2  # x的概率密度函数
    P_w1_x = (P_x_w1 * P_w1) / P_x  # 后验概率1
    P_w2_x = 1 - P_w1_x   # 后验概率2

    if P_w1_x > P_w2_x:  # 分类正常细胞
        data_w1 = np.append(data_w1, x_i)
        x1 = x1 + 1
    if P_w1_x < P_w2_x:  # 分类非正常细胞
        data_w2 = np.append(data_w2, x_i)
        x2 = x2 + 1

print("data_w1=", data_w1)
print("data_w2=", data_w2)

print("正常细胞个数:",x1)
print("非正常细胞个数:",x2)

plt.rcParams["font.family"] = "SimHei" # 添加了这句话可在图中显示中文
plt.rcParams["axes.unicode_minus"] = False # 添加了这一行使得负号可以显示

plt.scatter(range(x1), data_w1,marker='+',label='正常细胞')

plt.scatter(range(x2), data_w2,marker='o',label='非正常细胞')

plt.title('最小错误贝叶斯决策')
plt.legend()
plt.show()

最小错误结果图：

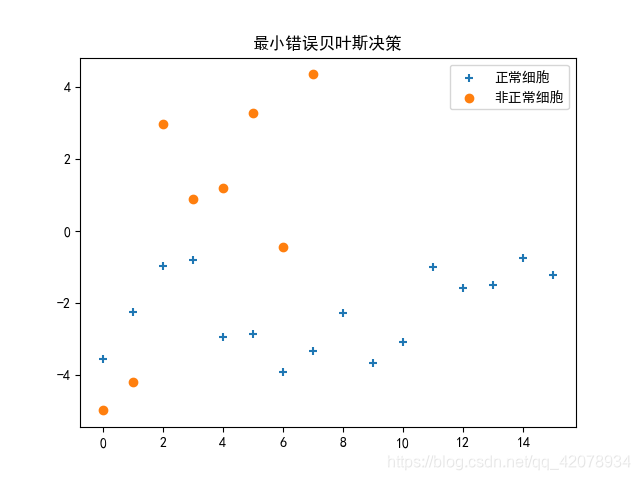
最小风险实验程序：

import numpy as np
import math
import matplotlib.pyplot as plt

x = [-4.9847, -3.5649, -2.2401, -0.9780, -0.8032, -2.9531,
     -2.8605, -3.9287, -3.3414, -2.2792, -3.6549,-3.0852,
     -4.1934, 2.9792, -0.9980, 0.8932, 1.1982, 3.2682,
     -1.5899, -1.4985, -0.7531, -0.4321, -1.2186, 4.3532]
y = range(24)
P_w1 = 0.92  # 先验概率1
P_w2 = 0.08  # 先验概率2

mean1 = -2  #均值1
std1 = np.sqrt(0.25)  #方差1
mean2 = 2   #均值2
std2 = np.sqrt(4)  #方差2

data_w1 = []  # 正常细胞
data_w2 = []  # 非正常细胞

x1 = 0
x2 = 0
for x_i in x:

    P_x_w1 = 1 / (std1 * pow(2 * math.pi, 0.5)) * np.exp(-((x_i - mean1) ** 2) / (2 * std1 ** 2))  # 条件概率密度函数1
    P_x_w2 = 1 / (std2 * pow(2 * math.pi, 0.5)) * np.exp(-((x_i - mean2) ** 2) / (2 * std2 ** 2))  # 条件概率密度函数2

    P_x = P_x_w1 * P_w1 + P_x_w2 * P_w2 # x的概率密度函数
    P_w1_x = (P_x_w1 * P_w1) / P_x  # 后验概率1
    P_w2_x = 1 - P_w1_x   # 后验概率2

    P_a1 = 0 * P_w1_x + 8 * P_w2_x
    P_a2 = 1 * P_w1_x + 0 * P_w2_x

    if P_a1 > P_a2:  # 分类正常细胞
        data_w1 = np.append(data_w1, x_i)
        x1 = x1 + 1 # 细胞个数
    if P_a1 < P_a2:  # 分类非正常细胞
        data_w2 = np.append(data_w2, x_i)
        x2 = x2 + 1 # 细胞个数 
print("data_w1=", data_w1)
print("data_w2=", data_w2)

print("正常细胞个数:",x1)
print("非正常细胞个数:",x2)

plt.rcParams["font.family"] = "SimHei" # 添加了这句话可在图中显示中文
plt.rcParams["axes.unicode_minus"] = False # 添加了这一行使得负号可以显示

plt.scatter(range(x1), data_w1,marker='+',label='正常细胞')
plt.scatter(range(x2), data_w2,marker='o',label='非正常细胞')

plt.title('最小风险贝叶斯决策')
plt.legend()
plt.show()

最小风险结果图：

本人能力有限，解释尚不清楚明了，如遇任何问题，大家可留言或私信。开源Matlab程序较多，大家按需参考学习使用。

本文希望对大家有帮助，当然上文若有不妥之处，欢迎指正。

分享决定高度，学习拉开差距