素数筛

基本介绍

素数问题是数学领域中的基本问题，也是程序设计或者面试笔试中的常见问题。计算机的诞生，让素数的计算过程大大加快。

本文是这段时间我个人学习素数相关知识的阶段性总结，也是对知识的记录和分享。

希望和大家一起学习、一起进步。以后还会陆续更新其他方面的知识。

首先，明确素数的定义：

质数(素数)是指在大于 1 的**自然数**中，除了 1 和它本身以外不再有其他因数的自然数。—“质数(素数)百度百科”

根据素数这一定义，可以提炼出几点内容

1. 素数是自然数，因此是整数
2. 素数是大于1的自然数，因此小于等于1的数字都不是素数（包括负数，0和小数）
3. 素数只有两个因数，1和自身
4. 结合1,2,3点，可以推断出，在自然数范围内，最小的素数是2

同时根据这一定义，发展出许多计算素数的方法，以下让我一一介绍。

小技巧，sqrt赋值给一个变量

算法

1、朴素算法

1.1、 试除法

朴素算法即最为直观的算法，这里只是根据素数的定义而设计的算法，没有涉及其他方面的知识。

根据素数的定义：素数只有两个因子，1和自身。

因此如果有其他因子的数字，都不是素数，这类数字称之为合数，概念上和素数相对。

从因子这一点入手，根据因子个数的多少，判断一个数字是否为素数。

这里采用试除法，正如字面意思一样，尝试相除。要判断n是否为素数，则在[2，n-1]范围内，逐一枚举数字，对每一素数，尝试用n去除。

• 如果可以被整除，则说明枚举的数字是n的因子。根据素数定义，数字n非素数
• 如果不可以被整除，则需要继续往后枚举，查看其他枚举数字相除之后的结果
  • 如果后面有可以被整除的数字，则结果和上面第一条一样。
  • 如果在[2，n-1]范围内都没有可以被整除的数字，则说明数字n在[1，n]范围内只有1和n两个因子，因此n是素数。

程序代码

时间复杂度为O(n)

#include<stdio.h>

int IsPrime(int n)
{
    int i;
//素数是指在大于 1 的自然数中，除了1和它本身以外不再有其他因数的自然数。
    if(n<2)//最小的素数是2，因此小于2的数字都是非素数。
        return 0;//加此判断是为了避免输入小于1的数而呈现出错误的结果
    else
    {
        for(i=2;i<n;i++)//逐个判断【2，n-1】范围内有无其他因子
        {//n=2时，直接跳过了此循环，返回结果1。
            if(n%i==0)
                return 0;
        }
        return 1;
    }
}

int main()
{
    int n;
    printf("请输入要检验的数字\n");
    while(scanf("%d",&n)!=EOF)
    {
        if(IsPrime(n)==1)
            printf("%d是素数\n\n",n);
        else
            printf("%d不是素数\n\n",n);
    }
    return 0;
}

1.2、优化方法一

上面的方法，是最容易想到的，但是效率并不高。如果在小范围内求素数可以，但n的规模一旦变大，就需要耗费很长的时间。

这里介绍两种优化方法，对上面的方法、程序进行一点优化。尽管这一点优化在大规模数据面前微不足道，但这种方式还是很值得去学习。

上面的程序，是在[2，n-1]范围内进行试除，那么是否可以缩小试除的范围呢？

我们注意到，一个数字x如果有其他因子a,b，则可以写成x=a*b的形式。a和b是一种负相关的关系，不会同时变大或者变小。当a最小为2,时，b最大为x/2。而a最大也只能为x/2，因为b最小只能为2。因此，可以推断出，x如果有其他因子，那么这个因子一定是在[2，x/2]范围内。基本原理和上面一致，都是试除法。在新的范围内如果没有可以整除的数字，那么就说明n没有其他因子，说明n是素数。

因此这样就把范围缩小到n/2，进行了一点优化

程序代码

时间复杂度为O(n/2)

#include<stdio.h>

int IsPrime(int n)
{
    int i,m;
    if(n<2)
        return 0;
    else
    {
        m=n/2;//其他代码都没有变，只是这里范围变动了一下
        for(i=2;i<=m;i++)//这里应该取等号，保证区间右侧大于等于左侧。不然可能会造成4的误判
        {//2和3不能保证区间右侧大于左侧，但是这两个数字是素数，因此没有关系。
            if(n%i==0)
                return 0;
        }
        return 1;
    }
}

int main()//主函数不变
{
    int n;
    printf("请输入要检验的数字\n");
    while(scanf("%d",&n)!=EOF)
    {
        if(IsPrime(n)==1)
            printf("%d是素数\n\n",n);
        else
            printf("%d不是素数\n\n",n);
    }
    return 0;
}

1.3、优化方法二

这里介绍另外一种优化方法

让我们换一种思路，不从范围入手，而是从数字的性质入手。

奇数和偶数是我们最常接触的一种分类方法，让我们从这里入手。

• 偶数是可以整除2的数字，那么这就说明偶数大概率不是素数（数字2除外），因为有个因子2。因此素数都是奇数

• 奇数不可以被2整除，也不可以被2的倍数整除。因此奇数不需要判定偶数因子，只需要判定奇数因子即可

素数都是奇数这个大家应该都认可，可能有的人对奇数不可以被2整除，也不可以被2的倍数整除这句话有点不理解，这里简单证明一下

设x是个奇数，那么x%2=1。设2的倍数为2*k。如果x可以被2*k整除，那么就是x%(2*k)=0。这里设商为a，即x/(2*k)=a

即x/2/k=a，那么把k移到右边就是x/2=k*a。这就说明x是偶数，与最开始的假设相悖。因此x是奇数时，不可以被2的整数倍整除。

经过上面两点，就可以减少判断的次数。当判定的数字是奇数时，就不需要在进行偶数因子的判定。奇数和偶数交错分布，那这样就可以少判断一半的范围，进行了一定程度的优化。

程序代码

时间复杂度为O(n/2)

#include<stdio.h>

int IsPrime(int n)
{
    int i;
    if(n<2||(n!=2&&n%2==0))//如果n小于2或者n是不等于2的偶数，则n不是素数
        return 0;//直接返回0
    else
    {//到这里的n都是奇数
        for(i=3;i<n;i+=2)//只需要判定奇数因子，从3开始
        {
            if(n%i==0)
                return 0;
        }
        return 1;
    }
}

int main()//主函数不变
{
    int n;
    printf("请输入要检验的数字\n");
    while(scanf("%d",&n)!=EOF)
    {
        if(IsPrime(n)==1)
            printf("%d是素数\n\n",n);
        else
            printf("%d不是素数\n\n",n);
    }
    return 0;
}

1.4、优化方法三

上面介绍了两种优化方法，这里第三种优化方法，就是把前面两种方法结合起来。在方法二的基础上，加上方法一。

即方法二是指判断n以内的奇数因子，加上方法一之后，就只判断n/2以内的奇数因子。两因子中一个因子取2时，另外一个因子才取n/2。而这里n是奇数，不可以取2，因此另外一个因子是小于n/2的。

注意：

• 并不是什么优化操作都可以叠加使用，要注意彼此之间的原理，是否冲突，是否会影响正确性
• 这里优化方法一是从因子分布区间入手，无论n如何，都成立。优化方法二是从n的性质入手。两者之间并不冲突
• 优化方法一中，因子的范围是[2，n/2]，极端情况下分布在两端，因此两端都可取。而在优化方法二中，因为左侧不可取，所以右侧也不可取，所以因子范围是(2，n/2)

程序代码

时间复杂度O(n/4)

#include<stdio.h>

int IsPrime(int n)
{
    int i,m;
    if(n<2||(n!=2&&n%2==0))//如果n小于2或者n是不等于2的偶数，则n不是素数
        return 0;//直接返回0
    else
    {//到这里的n都是奇数
        m=n/2;//加了这一步
        for(i=3;i<m;i+=2)//范围左端不取2，因此右端不取m=n/2
        {
            if(n%i==0)
                return 0;
        }
        return 1;
    }
}

int main()//主函数不变
{
    int n;
    printf("请输入要检验的数字\n");
    while(scanf("%d",&n)!=EOF)
    {
        if(IsPrime(n)==1)
            printf("%d是素数\n\n",n);
        else
            printf("%d不是素数\n\n",n);
    }
    return 0;
}

2、优化的朴素算法

2.1、算法介绍

上面介绍了三种优化方法，实际上是两种，但最好的情况也只是把时间复杂度从O(n)降到了O(n/4)。

那么是否有更好的优化方法呢？

在上面的方法二中，因子虽然都是在[2，n/2]这个范围内，但因子在数轴上，总是一个前一个后。在此范围内，如果前半部分都没有找到因子，那么必然后半部分的数字也不是因子。那么这个前后的分界线在哪里呢？

聪明的你可能想到，或者已经知道了，这个分界线就是根号n，下面用sqrt(n)表示。

这里对朴素的素数判定方法进行一点优化。

数字的因子有一个特点，就是成对出现的（两个成对的因子相乘才等于原来的数字），并且成对出现的因子分布在sqrt(n)的两侧

简单证明一下为什么一定分布在sqrt(n)两侧：假设k=sqrt(n)，那么k*k=n

如果成对的两个因子不分布在k的两侧，比如同时大于k或者同时小于k。因为k*k=n，那么这两个成对因子相乘的结果要么是大于n，要么是小于n。既然相乘结果都不是n，那么就不是n的因子，则与最开始的假设相悖。

得到上面的性质之后，就可以对朴素算法再进行优化。

因为因子是成对出现，并且分布在sqrt(n)两侧。那么判断数字有无其他因子的时候，判断范围可以从[2，n-1]缩小到[ 2，sqrt(n) ]。（如果[2， sqrt(n) ]没有因子，那么[ sqrt(n) ， n-1]也不会有因子。原因就是前面提到的，因子是成对出现的）

程序代码

时间复杂度O(sqrt(n))

#include<stdio.h>
#include<math.h>//sqrt的头文件

int IsPrime(int n)
{
    int i,m;
    if(n<2)
        return 0;
    else
    {
        m=(int)sqrt((double)n)//sqrt函数中形参类型是double类型，这里进行一下转换防止出错
        for(i=2;i<=m;i++)//缩小判断范围，判断2-sqrt(n)范围内有无其他因子即可
        {//数字的因子是成对出现的，且分布在sqrt(n)两侧。因此判断一侧没有因子，就可知另一侧也没有
            if(n%i==0)//其他步骤不变
                return 0;
        }
        return 1;
    }
}

int main()//主函数不变
{
    int n;

    printf("请输入要检验的数字\n");
    while(scanf("%d",&n)!=EOF)
    {
        if(IsPrime(n)==1)
            printf("%d是质数\n\n",n);
        else
            printf("%d不是质数\n\n",n);
    }
    return 0;
}

关于Isprime函数，其中还可以另外一种写法，就不需要用sqrt函数开根

int IsPrime(int n)
{
    int i;
    if(n<2)
        return 0;
    else
    {//函数其他部分不变
        for(i=2;i*i<=n;i++)//这里用i替代了开根号的过程
        {//这里应该取等号，需要取到i=sqrt(n)这个值
            if(n%i==0)
                return 0;
        }
        return 1;
    }
}

2.2、小优化方法

这里可以利用之前提到过的1.3中的优化方法再进行优化。只对奇数进行素数判断，并且只判定奇数因子。

原因是什么？这里再简单重复一遍

• 偶数（除了2以外）必然不是素数，素数必然是奇数
• 奇数不能被2的整数倍整除，因此奇数的因子中必然没有2的整数倍(偶数)，也就不需要判定偶数是否为奇数的因子

程序代码

int IsPrime(int n)
{
    int i;
    if(n<2||(n!=2&&n%2==0))//n小于2或者n是不等于2的偶数，必然非素数
        return 0;
    else//这里n都是奇数
    {//这里使用上面刚提到的写法，用i代替开根号的过程
        for(i=3;i*i<=n;i+=2)//这里注意循环条件
        {//2必然不是因子，从3开始，每次递增2，直到sqrt(n)为止
            if(n%i==0)
                return 0;
        }
        return 1;
    }
}

3、素数筛-埃氏筛(埃拉托斯特尼筛法)

这里介绍另外一种找素数的方法。

上面的朴素算法以及各种优化方法，都是对给定的单一数字进行判断，从而得知这个数字是否为素数。但在实际问题中，往往需要获取一个区间内所有素数，或者在短时间内多次查询判断。应对这样的需求，我们会进行预处理：对某一区间进行素数挑选，把素数挑选出来，存储到另外一个地方或者标记起来。

要实现这样的预处理，使用上面的朴素算法，就需要双层循环，这样时间复杂度大概是O(n^2)

接下来介绍的这两种算法，正好是把某一区间内的素数都筛选出来，且时间复杂度也不高。

3.1、简单介绍–引入

让我们再次回顾素数(质数)的定义

质数(素数)是指在大于 1 的**自然数**中，除了 1 和它本身以外不再有其他因数的自然数。—“质数(素数)百度百科”

上面的朴素算法，我们是尝试把数字拆分为因子相乘的形式，对范围区间内的数字进行判断时，，则需要对每个数字都进行拆分，那么我们是否可以使用另外一种方式呢？

这里我们选择另外一种方式：反向构造。

我们事先不知道一个数是否为素数，但是我们可以创造出合数（非素数）。

数字可以划分为素数和合数两大类，那么当我们把某一范围内的合数都标记出来，则剩下的数字就是素数。

如何构造合数呢？在大于1的数字中任取两个数字a，b相乘即可，这样得到的结果c必然有1，a，b，c四个因子（当a=b时为三个因子）那么c必然是合数

总结成算法就是

1. 设定两个数组，一个数组包括范围内的所有数字，用来标记此数字是否被访问过；另外一个数组用来存储已经筛选出来的素数（如果仅仅是查询某个数是否为素数，则访问数组就可以实现这个功能，素数数组是方便筛选过程结束后可以输出筛选出的素数）
2. 将访问数组中访问标记设为未访问，将素数数组清空，将0，1等非素数访问标记设为已访问（素数标记是设为未访问还是已访问，根据自己的逻辑习惯设定）
3. 从2开始循环，直到范围的上界，判断每一个数字是否被访问过，访问过的是非素数（合数），未访问过的是素数
4. 接着对这个数字进行倍增操作，从两倍开始，直到若干倍后到达上界为止，这其中得到的数字结果的访问标记都设为已访问。重复步骤3,4，直至3中循环结束

这里步骤4中是第二个循环，用来进行倍增操作，凡是在此过程中得到的数字，都是构造出来的合数。而步骤3中，循环到当前数字未被访问过，则此数字是素数。因为如果此数字是合数的话，那么它的因子一定是小于自身的。那么在前面从小数开始循环的时候，就会遇到因子，更会在这个因子倍增的过程中，把数字给标记掉。所以如果步骤3访问当某个数字是未标记时，那么这个数字一定是素数。

举例说明：12是合数，有2,3,4,6；从小数开始循环、倍增时，2倍增时会把12标记掉，同样地，3,4,6也会把12标记掉。所以如果访问到a未被标记，那么a一定是素数

这个算法的好处就是，利用了一次倍增，得到了后面若干个数字的结果。循环到这些数字的时候，就不再需要花时间去计算，直接可以得到结果。这里用了一个必不可少的标记数组，花费了一定的空间。**这里实际上就是典型的用空间来换取时间。**花费更多的内存空间，来换取时间的减少。时间和空间的取舍，也讲求经济性

程序代码

这里就不提时间复杂度了。这里整个过程像个筛子一样，把不要的合数筛下去，剩下的就是所需的素数。

#include<stdio.h>
#include<string.h>//memset函数的头文件

//设定一个宏，定义数组大小
#define maxn 20010

int vis[maxn];//vis用来判断数字是否访问过
int prime[maxn];//prime用来存储筛选出来的素数


int sieve(int n)
{
    int i,j,k;
    k=0;//i用来控制逐个访问，j用来第二轮标记，k用来标记prime数组位置
    //这里在函数中置为0，保证每一次函数调用时都清空，不会受到上次使用完后的结果
    //理论上需要这样做，但是在此程序中可以省略，因为数字范围彼此之间是子集的关系，而范围的改变不会改变数字的性质
    memset(vis,0,sizeof(int)*maxn);//将访问数组清零。可以使用short或者C++的bool类型节省内存、
    vis[0]=vis[1]=1;//将0和1标记为已访问，不标记其实也可以，因为我们素数的计数是从2开始
    for(i=2;i<=n;i++)//从最小的素数2开始筛选，2以下就没必要筛选
    {
        if(vis[i]==0)//这个数是目前最小的，且未被访问过的
            prime[k++]=i;//因此这个数是素数
        for(j=2;i*j<=n;j++)//j表示倍数，从两倍开始倍增，直到上界为止
            vis[i*j]=1;//将倍数标记为已访问
    }
    return k;//返回范围内素数的个数
}

void print(int k)//打印结果函数
{
    int i;
    for(i=0;i<k;i++)
    {
        printf("%5d ",prime[i]);//每个数字占5个宽度，右对齐，保持输出结果整洁
        if((i+1)%5==0)//每五个为一组换行
            printf("\n");
    }
    printf("\n\n");
}

int main()
{
    int n;//求n以内的素数
    int k;//保存返回的素数个数
    while(scanf("%d",&n)!=EOF)
    {
        k=sieve(n);
        if(k==0)
            printf("(1-%d]范围内没有素数\n",n);
        else
            printf("(1-%d]范围内的素数有:\n",n);
        print(k);
    }
}

函数中另外一种写法

int sieve(int n)
{
    int i,j,k;
    k=0;
    vis[0]=vis[1]=1;
    for(i=2;i<=n;i++)
    {
        if(vis[i]==0)
            prime[k++]=i;
        for(j=i+i;j<=n;j+=i)//这里j表示i的倍数结果，每次加i相当于加一倍
            vis[j]=1;
    }
    return k;
}

这里给出1-100范围内的素数以供检验

范围	素数
(1,10]	2,3,5,7
(10,20]	11,13,17,19
(20,30]	23,29
(30,40]	31,37
(40,50]	41,43,47
(50,60]	53,59
(60,70]	61,67
(70,80]	71,73,79
(80,90]	83,89
(90,100]	97

3.2、埃氏筛

上面的构造方法，是对每个数字都进行倍增，但实际上这样的效率很低，造成了很多的重复。

比如说对2进行倍增之后，会对4,6,8,10,12,14,16,18,20,22,24,26,28,30等等进行标记

而轮到4的时候，就会对8,12,16,20,24,28,32等等进行倍增

可以发现这其中有大量的重复，这相当于重复标记了，并且这只是举了2和4的例子，后面还有更多的重复。而造成重复的根本原因就是后面进行倍增的数字，如4，是前面数字倍增后的结果。可以想到，4的倍数，8的倍数，必然是2的倍数，那么使用4,8进行倍增无疑是以不同的步长重复标记。4和8这类数字，都是已经被标记过的数字，换言之也就是合数。那么就是不应该对合数进行倍增，因为合数必然是某个素数的倍数(一定是某个素数的倍数吗？必然是，这是一个递归定义，必然终结于素数)。对合数进行倍增，就是在重复标记。

这里引入一个数学定理–唯一分解定理，也是算术基本定理

算术基本定理可表述为：任何一个大于 1 的自然数 N, 如果 N 不为**质数**，那么 N 可以唯一分解成有限个质数的乘积—-唯一分解定义百度百科

因此合数的因子中一定有个素数，循环是从小到大的，那对最小的素数进行倍增之后，就不需要对其倍数结果进行倍增。（即对3进行倍增之后，就不在需要对6,9,12进行倍增）因此上面的算法，进行一点改进，就可以大大提升效率，而这种算法就是埃拉托斯特尼筛法，简称埃氏筛。

程序代码

时间复杂度O( N log(logN) )*

#include<stdio.h>
#include<string.h>//memset函数的头文件

//设定一个宏，定义数组大小
#define maxn 20010


int vis[maxn];//vis用来判断数字是否访问过
int prime[maxn];//prime用来存储筛选出来的素数

//埃氏素数筛函数
int Eratosthenes_sieve(int n)//这里用了英文全称，平时用sieve等命名就好
{
    int i,j,k;
    k=0;
    memset(vis,0,sizeof(int)*maxn);
    vis[0]=vis[1]=1;
    for(i=2;i<=n;i++)//从最小的素数2开始筛选，2以下就没必要筛选
    {
        if(vis[i]==0)//这个数是目前最小的，且未被访问过的
        {
            prime[k++]=i;//因此这个数是素数,存储起来
            for(j=2;i*j<=n;j++)//这里的改变就是把损坏放入if判断语句之内
                vis[i*j]=1;//只对素数进行倍增筛选，其他基本不变
        }
    }
    return k;//返回范围内素数的个数
}

void print(int k)//打印结果函数
{
    int i;
    for(i=0;i<k;i++)
    {
        printf("%5d ",prime[i]);//每个数字占5个宽度，右对齐，保持输出结果整洁
        if((i+1)%5==0)//每五个为一组换行
            printf("\n");
    }
    printf("\n\n");
}

int main()
{
    int n;
    int k;//保存返回的素数个数
    while(scanf("%d",&n)!=EOF)
    {
        k=Eratosthenes_sieve(n);
        if(k==0)
            printf("(1-%d]范围内没有素数\n",n);
        else
            printf("(1-%d]范围内的素数有:\n",n);
        print(k);
    }
}

3.3、优化方法一

再次观察上面的程序，会发现优化之后，仍然会有重复标记的情况出现，这是为什么呢？

仔细观察之后，发现是倍增的起点选择问题。上面的程序每次都是从2倍开始倍增，如果想要不重复标记，则需要从 i 倍开始倍增。

假设现在 i=b，如果从2倍开始倍增，将会标记b*2这个数，而这个数实际上在2倍增b倍的时候，就已经标记了。所以每次倍增应该从 i 开始，从 i^2开始标记。

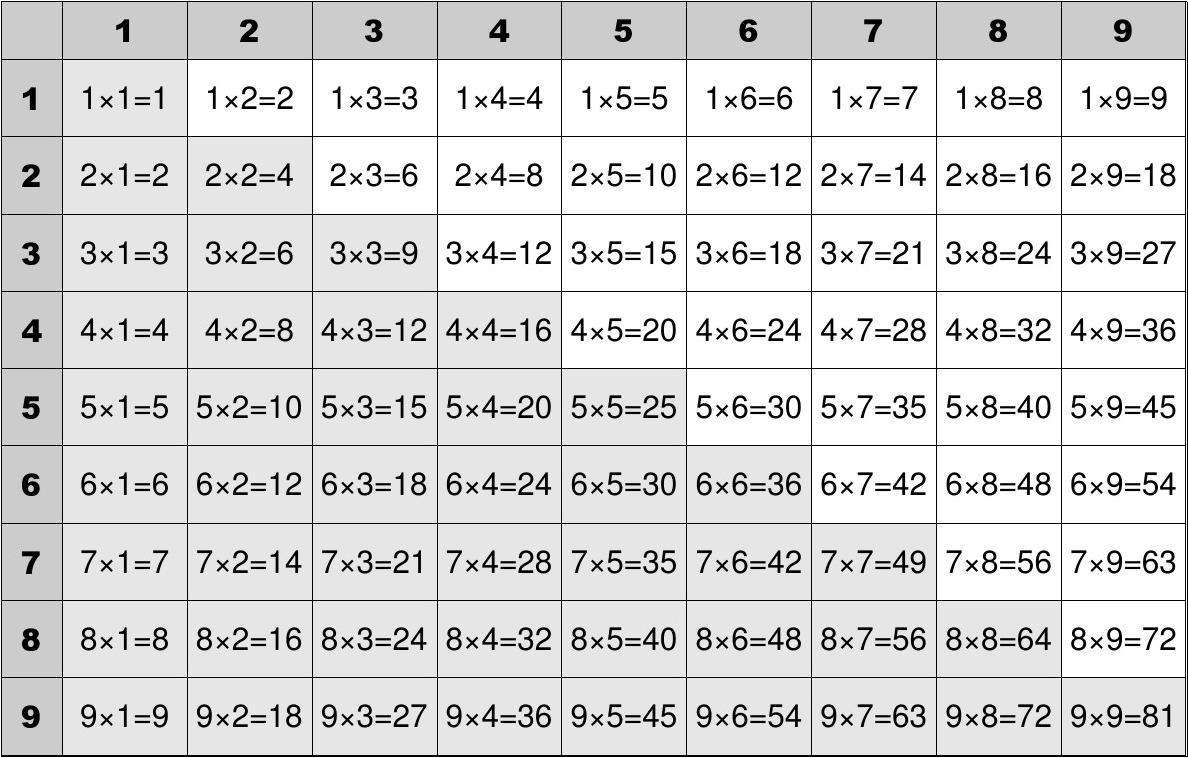
这就相当于这张九九乘法表，如果没有从 i*i 开始，从2倍开始，就会标记第2列到第9列中的所有内容。如果从 i*i 开始，那标记的就是对角线部分+表格的上三角白色部分。这样就很明显看出，小小的一点改动，就节约了将近一半的计算。

程序代码

这里就不提时间复杂度了

//埃氏素数筛函数
int Eratosthenes_sieve(int n)
{
    int i,j,k;
    k=0;
    memset(vis,0,sizeof(int)*maxn);
    vis[0]=vis[1]=1;
    for(i=2;i<=n;i++)
    {
        if(vis[i]==0)
        {
            prime[k++]=i;
            for(j=i;i*j<=n;j++)//仅仅是这里，把j=2改为j=i
                vis[i*j]=1;
        }
    }
    return k;
}

3.4、优化方法二

这一步，让我们继续优化。

上一步，我们是优化到，只对素数进行倍增。结合朴素算法中的优化方法二：素数一定是奇数。我们是否可以再进行优化呢？

这里我们可以对上面的第一重循环进行优化，只判断奇数是否为素数，再进入第二重循环。

那么这种方法是否正确呢？先让我们看看如果这样做时候，会发生什么：

• 2以上的奇数(3,5,7,9等等)的倍增过程不受影响
• 2以上(包括2)的偶数，将不再倍增

第一点不影响算法的正确性，第二点，2以上的偶数，就是2的倍数，按照上面的优化过程，也不会倍增，这一点也不影响算法的正确性。而关于2的倍增，2的倍增都是偶数，并且全都不是素数，这一点进行一下预处理即可避免。因此我们可以进一步优化，只对奇数进行判断。

程序代码

这里也不提时间复杂度了

//埃氏素数筛函数
int Eratosthenes_sieve(int n)
{
    if(n<2)//之前不加上这句，是因为可以通过循环条件进行判定
        return 0;//现在前面有预处理，需要先判断
    int i,j,k;
    k=0;
    memset(vis,0,sizeof(int)*maxn);
    vis[0]=vis[1]=1;
    vis[2]=0;//这步可以省略，加上后方便理解
    prime[k++]=2;//这步很重要，不能省略，容易忘记
    for(i=3;i<=n;i+=2)//只对奇数判定，因此从3开始，步长为2
    {
        vis[i+1]=1;//把偶数的标记补上
        //这里存在大于n的风险，因此需要把数组开大一点
        //如果是i-1，则当n为偶数时，n的标记不能补上
        if(vis[i]==0)
        {
            prime[k++]=i;
            for(j=i;i*j<=n;j++)//这里把j=2改为j=i
                vis[i*j]=1;
        }
    }
    return k;
}

这里的优化并不是很明显，只是在循环中省略了判断偶数是否为素数这一过程

虽然针对时间要求高的题目有更好的算法去解决应对，但这种优化方式还是值得学习一下，一方面作为了解，成为知识储备，另一方面开拓思维。

3.5、优化方法三

埃氏筛的平方优化

让我们继续深入，看看有没有其他优化的方法

上面的朴素算法中，可以把O(n)的时间复杂度优化到O( sqrt(n) )。不需要对[2，n-1]中每个数字都判断是否为因子，只需要判断[2，sqrt(n) ]范围内即可，因为因子是成对出现，并且分布在sqrt(n)两侧的。因此只需要对一侧进行判断，如果这一侧的数字不是因子，那么另外一侧的数字也不是因子，这就可以说明这是素数。

那么这种方式是否也可以应用到埃氏筛中呢？答案是可以，不妨尝试证明一下

简单证明一下：一个范围内的数字分为素数和合数，合数有多个因子(至少3个)，且因子都分布在sqrt(n)两侧。如果左侧范围数字不是因子，那么由于因子是成对出现的，则右侧范围中也没有因子，因此可以说明这个数字是素数。回顾埃氏筛的过程，使用素数去倍增来筛选出合数。

一个合数x，必然有一个因子在[2，sqrt(x) ]范围内，当我们在这个范围内循环倍增时，必然会经过x的因子，那么在之后的倍增过程中，就得到合数x，并把合数x进行标记。（值得说明的一点是，这里的合数x是奇数，因为偶数的合数我们早就已经人为标记过了）

程序代码

时间复杂度暂时不提

//埃氏素数筛函数
int Eratosthenes_sieve(int n)
{
    if(n<2)
        return 0;
    int i,j,k;
    k=0;
    memset(vis,0,sizeof(int)*maxn);
    vis[0]=vis[1]=1;
    vis[2]=0;
    for(i=4;i<=n;i+=2)//这里把偶数全部标记为1，非素数
        vis[i]=1;

    for(i=3;i*i<=n;i+=2)//这里只是把 i<=n 改为 i*i<=n
    {
        if(vis[i]==0)//对素数进行倍增
        {
            for(j=i;i*j<=n;j++)//这里把j=2改为j=i
                vis[i*j]=1;
        }
    }

    //上面的循环，只循环到sqrt(n),因此要存储范围内的素数，需要重头遍历一遍
    prime[k++]=2;
    for(i=3;i<=n;i+=2)//只遍历奇数
    {
        if(vis[i]==0)
            prime[k++]=i;
    }
    return k;//返回素数的个数
}

这个程序后面补了一个循环，和之前的程序相比，效率似乎反而降低了。之前的程序，在一遍循环中完成标记和存储两个任务，而这个程序需要三个循环。

我没有测试过不同程序的具体耗时，无法给出一个准确的比较结果。但这个程序适合于只标记，不存储的情况，这样就可以少一个循环。另外这个程序的效率还是高的，时间主要节约在第二层循环中：其他程序，对每个素数都要进行倍增，而这个程序只对sqrt(n)内的素数进行倍增，当数据量越大，则两者之间素数的个数就差的越大，继而倍增的次数就相差越大。就比如说n=20的时候，前者需要对2,3,5,7,11,13,17,19倍增，而后者只需要对2,3进行倍增。n=100时差距就更大了，前者需要对25个素数进行倍增，后者只需要对2,3,5,7进行倍增。

4、素数筛-欧拉筛

埃氏筛有一个问题，就是一个数字可能会被重复筛除。比如说12，可能在2的时候被筛除，可能在6的时候被筛除。即使进行了上面的优化(只对素数进行倍增)，也还是会被3筛除。这里只是举一个例子，当一个合数数字越大，其中的素因子越多的时候，则重复被筛除的次数就越多。

欧拉筛就是要解决这个问题，保证每个合数只被筛选一次，从而提高效率和运行速度，那么怎么做呢？

根据唯一分解定理可知，每个合数都有一个最小素因子。而欧拉筛的基本思想是，让每个合数被其自身的最小素因子筛选，而不会被重复筛选。欧拉筛的框架和埃氏筛大致相同，区别点在于第二层循环对倍增过程的操作。

埃氏筛是，只要是素数就进行倍增。而欧拉筛是用当前遍历到的数字i，去乘以已经在素数表中的素数。

首先，这样就保证了是以素数进行倍增，相较于使用任何数字进行倍增的情况，是已经优化过了。比如说此时i=6，前面有素数2,3,5。在欧拉筛中就是用2,3,5去乘以6，进行倍增筛除。因为 i 是从小到大进行循环，会乘以前面的每一个素数，这就保证了每个素数的倍数都不会被错过。并且每个素数的倍增过程都是从平方开始，就和前面埃氏筛优化方法一种一样，可以有效避免重复。

举例说明：现在 i 循环到6，前面有素数2,3,5，这三个素数，都是从2*2，3*3，5*5开始倍增的，不会出现2*3，3*2的情况同时出现。

那么至于怎么保证每个合数只被标记一次呢？这里我们先看核心代码

//欧拉筛函数
int Euler_sieve(int n)
{
    int i,j,k;
    k=0;//保存素数的个数
    memset(vis,0,sizeof(int)*maxn);//初始化数组
    for(i=2;i<=n;i++)
    {
        if(vis[i]==0)//i是素数，则存起来
            prime[k++]=i;
        for(j=0;j<k;j++)//进行倍增，用i去乘以i之前(包括i)的素数
        {
            if(i*prime[j]>n)//倍增结果超出范围，退出
                break;

            vis[ i*prime[j] ]=1;//将倍增结果进行标记

            if(i%prime[j]==0)//i是前面某个素数的倍数时，也需要退出
                break;
        }
    }
    return k;
}

代码中，最关键是这条语句

if(i%prime[j]==0)
    break;

这条语句的加入，保证了每个合数只会被筛除一次，不会被重复筛除。那么为什么？

当 i 可以整除素数表中某个素数时，那么 i 就不需要在往后乘以其他素数了，因此往后乘以得到的结果，会以另外一种方式得到。

用公式解释就是

当 i%prime[j]==0时，i*prime[j+1]的结果，可以通过另外一种方式得到，比如说 x*prime[j]，即x*prime[j]=i*prime[j+1]

i%prime[j]==0 说明prime[j]是i的一个素因子，并且是最小的素因子(因为是最早接触的素因子)，所以i可以表示为a*prime[j]的形式

那么i*prime[j+1]即等于a*prime[j]*prime[j+1]的，所以i*prime[j+1]的结果，也是prime[j]的倍数，当i往后继续循环到x的时候，就会有x*prime[j]出现，就把之前的结果给补回来了。

prime[j+1]是这种结果，往后的j+2,j+3等等也是类似的结果，因此这里就可以退出循环，等到i循环到x的时候，再把这个合数结果筛除。

这里合数到了prime[i]就退出了，因此后面的素数没有倍增的机会，即这个合数不会被其他素因子倍增到。(不会出现2*6=3*4=12等重复标记的情况出现)

因此每个合数只被其最小的素因子筛除，不会被其他素因子筛除，因此欧拉筛中每个合数只会被筛除一次，不会被重复筛除。

举例说明就是

比如i=12，此时素数数组中有素数2,3,5,7,11

2*12=24，把24筛除了，但是判定12可以整除2，2是12的最小素因子(是因子，且是素数因子)，此时循环退出。

为什么呢？

因为12*3=36这个结果可以通过12的最小素因子2，以其他方式得到。36这个结果，当x=18时可以通过18*2得到。同样的，后面的素数*12得到结果，也可以通过另外的x与2相乘得到。比如12*5=60，可以通过30*2得到

上面使用公式进行了解释，这里再说明一下，2是12的最小素因子，12可以被2整除，那么12乘以其他的素数得到的结果，也同样可以被2整除，得到的商就是那个x。因此这里就不再第二层循环中往后乘，而是跳出第二层循环，进入第一层循环。等到第一层循环中循环到了合适的i=x时，就可以复现此时的结果。因此这个合数并不会被忽略，而只是筛除的过程滞后了。

这样的滞后操作，保证了每一个合数，只被筛除一次，不会被重复筛除。这种筛除方式，就是欧拉筛算法最前面提到的，使用最小素因子筛除。

6、区间筛

这里挖个坑，过段时间补上

6、素数筛总结

这里给出一点编程小技巧：

1. 如果是用作标记，可以选择用更小的数据类型进行存储，比如说short，bool类型。甚至经过巧妙设计之后，可以使用 位 来标记
2. 循环中尽量不要出现表达式，可在外面用变量存储表达式的值，再放入循环中。避免每循环一次，都要重新计算一次

求素数的几种方法：

1. 判断单个数字是否为素数
   1. 试除法（穷举法）
      1. 优化方法一：范围缩小到n/2，原因是合数因子范围为[2，n/2]
      2. 优化方法二：使用奇偶数性质优化，原因是素数是奇数，奇数不能被2的整数倍(偶数)整除
      3. 优化方法三：上面两种方法结合
   2. 优化到sqrt(n)的试除法，原因是因子成对且分布在sqrt(n)两侧，检测一侧即可
      1. 优化方法一：使用奇偶性质优化，原因不重复
2. 筛选区间范围内的素数
   1. 埃氏筛
      1. 引入中，利用任何数字的倍数都不是素数的性质
      2. 埃氏筛，只对素数进行倍增，利用唯一分解定理，合数必然可以分解出素因子
      3. 优化方法一：倍增从 i 开始
      4. 优化方法二：只对奇数进行素数判定，以为素数一定是奇数
      5. 优化方法三：开平方优化，同样是因为数字的因子成对出现且分布在sqrt(n)两侧
   2. 欧拉筛
      1.

这里有多种优化方法，有的甚至是多种优化方法复合使用。但在复合使用前，需要先判断一下这样做是否会影响程序的正确性。