1 基础

熵年岁很大，建国前一年香农提出来的的，成精了。熵指的是体系的混乱的程度，越乱越大。图像熵是图像特征的一种统计形式,反映了图像中平均信息量的多少,能够反映图像各像素点的分布复杂程度。

1.1 图像一维熵

只能表示图像灰度值的聚集特征，不能表征空间特征。公式:
$$H=-\sum _{i=0}^{255}lo{g}_2{p}_i$$
其中Pi表示图像中灰度值为i(0≤i≤255)的像素所占的比例,熵非负。(公式中使用Log或者ln均可，不同文献描述不一样)

1.2 二维熵

为表征灰度信息的空间特征,引入图像的像素点与该点的邻域信息,构成一个新的特征二元组,记为(i,j)；其中i表示像素的灰度值(0≤i≤255), j表示邻域灰度均值(0≤j≤255)。同时，为了反映某像素位置上的灰度值与其周围像素的灰度分布的综合特征,定义图像中f(i,j)的发生的概率为$P_{ij}$。
$$P_{ij}=f(i,j)/(WH)$$
其中f(i,j)为特征二元组(i,j)出现的次数,W和H为图像尺寸,公式：
$$j=\frac{{\sum }_{k=1}^{8}j(k)}{8}$$
此处设置为8的原因是选择了9宫格领域，除了目标像素点，邻域总共为8个像素
$$H=-\sum _{i=0}^{255}\sum _{j=0}^{255}{p}_{ij}lo{g}_2{p}_{ij}$$
邻域随便一点，反正求个均值就行了，九宫格，菱形，近圆，得为奇数，不理解就画图…（本文按九宫格火锅来写的）

• 代码中的计算$Pij$这里使用len(F)有点不合适，最好换成img的长宽乘积。只是因为本例自己采用的图像的特殊性，没有重复的(i,j)对，所以len(F)=len(IJ)=len(arr)=256=img.shape[0]*img.shape[1]。

1.3 局部熵

就是把图分成一个个区域，分别计算再融合成信息分布图，有点类似heatmap.

2 python 实现

2.1 一维熵

import cv2
import matplotlib.pyplot as plt
import numpy as np
import math


def calc_array():
    # img = cv2.imread('20201210_3.bmp',0)
    # img = np.zeros([16,16]).astype(np.uint8)

    a= [i  for i in range(256)]
    img = np.array(a).astype(np.uint8).reshape(16,16)

    hist_cv = cv2.calcHist([img],[0],None,[256],[0,256]) #[0,256]的范围是0~255.返回值是每个灰度值出现的次数

    # plt.subplot(111)
    # plt.plot(hist_cv)
    # plt.show()
    
    P= hist_cv/(len(img)*len(img[0]))  #概率
	E = np.sum([p *np.log2(1/p) for p in P])
    print(E) #熵
calc_array()

2.2 二维熵

import cv2
import matplotlib.pyplot as plt
import numpy as np
import math

def calc_2D_Entropy():
    '''
    邻域 3*3的小格子
     __ __ __
    |__|__|__|
    |__||||__|
    |__|__|__|
    角点
     __ __
    ||||__|
    |__|__|
    边
     __ __
    |  |__|
    ||||__|
    |__|__|
    '''
    a= [i  for i in range(256)]
    img = np.array(a).astype(np.uint8).reshape(16,16)

    N = 1 # 设置邻域属性，目标点周围1个像素点设置为邻域，九宫格，如果为2就是25宫格...
    S=img.shape
    IJ = []
    #计算j
    for row in range(S[0]):
        for col in range(S[1]):
            Left_x=np.max([0,col-N])
            Right_x=np.min([S[1],col+N+1])
            up_y=np.max([0,row-N])
            down_y=np.min([S[0],row+N+1])
            region=img[up_y:down_y,Left_x:Right_x] # 九宫格区域
            j = (np.sum(region) - img[row][col])/((2*N+1)**2-1)
            IJ.append([img[row][col],j])
    print(IJ)
    # 计算F(i,j)
    F=[]
    arr = [list(i) for i in set(tuple(j) for j in IJ)] #去重，会改变顺序，不过此处不影响
    for i in range(len(arr)):
        F.append(IJ.count(arr[i]))
    print(F)
    # 计算pij
    P=np.array(F)/(img.shape[0]*img.shape[1])#也是img的W*H

    # 计算熵
    
	E = np.sum([p *np.log2(1/p) for p in P])
    print(E)

calc_2D_Entropy()

2.3 局部熵

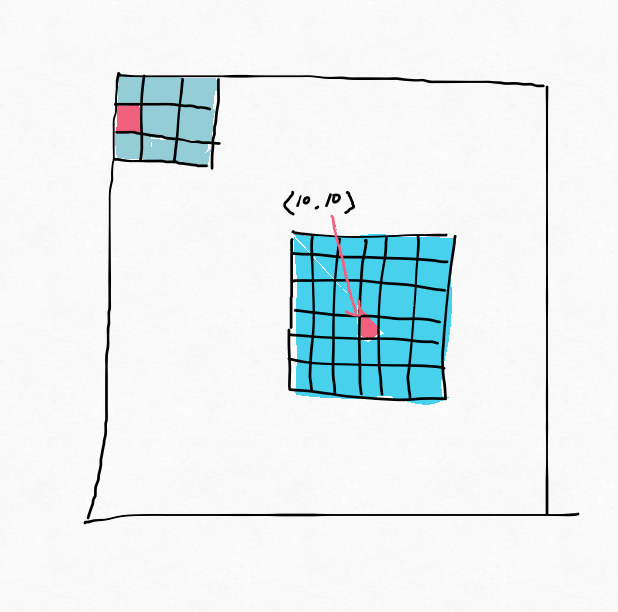
可以当作是局部的确的一维熵，再拼起来。如下图(N=3,计算的是6*6这个局域)，注意边缘点边界

from PIL import Image
import numpy as np
from matplotlib import pyplot as plt

# 熵
def entropy(signal):
        lensig=signal.size
        symset=list(set(signal))
        propab=[np.size(signal[signal==i])/(1.0*lensig) for i in symset]#每个值的概率
        ent=np.sum([p*np.log2(1.0/p) for p in propab])
        return ent
# 读图，也可以用Opencv啥的
colorIm=Image.open('20201210_3.bmp')
colorIm=np.array(colorIm)
# 灰度
greyIm=colorIm.convert('L')
greyIm=np.array(greyIm)
N=3
S=greyIm.shape
E=np.array(greyIm)

#以图像左上角为坐标0点
for row in range(S[0]):
    for col in range(S[1]):
        Left_x=np.max([0,col-N])
        Right_x=np.min([S[1],col+N])
        up_y=np.max([0,row-N])
        down_y=np.min([S[0],row+N])
        region=greyIm[up_y:down_y,Left_x:Right_x].flatten()  # 返回一维数组
        E[row,col]=entropy(region)

plt.subplot(1,3,1)
plt.imshow(colorIm)

plt.subplot(1,3,2)
plt.imshow(greyIm, cmap=plt.cm.gray)

plt.subplot(1,3,3)
plt.imshow(E, cmap=plt.cm.jet)
plt.xlabel('6x6 邻域熵')
plt.colorbar()

plt.show()

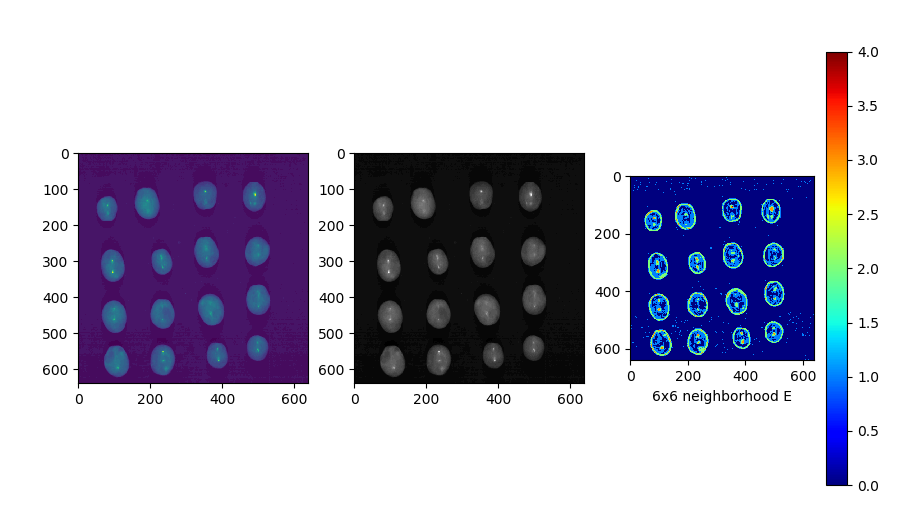
结果如图，可知同内容部分熵较低

2022/4/14 已更新

代码中添加了注释，二维熵公式描述做了补充，欢迎大家指正。前期可能是我描述不太清楚。