本系列将从下面几方面谈谈最近的一点点收获

令声明：本文主要是对我找到的一个莫名其妙国外英文pdf文件的学习与解读，因为我也没有找到他的出处（也没作者也没学校），所以我仅以此段文字向这个未知的作者致敬。本文主要处于科普类的理解，列出的主要算法并没有给出详细解读，从csdn上找到了各处有效的不错的超链接，附在对应算法后，方便读者查阅，侵删。

频繁模式（Frequent Patterns）

搜索优化算法（ Search Optimization Algorithms）

频繁项集挖掘（Frequent Itemset Mining）

序列挖掘（Sequence Mining）

频繁模式

过度进食、睡眠、吸烟、饮酒、压力、心脏病发作、睡眠、暴饮暴食、吸烟、饮酒、压力？？？？这些词之间到底有什么值得我们去发掘。

• 频繁模式挖掘是识别那些经常发生的事件、任务、实体等的过程
• 尽管其搜索空间简易，但依旧在数据挖掘中占有重要的一席位

定义

• 事务（Transaction）：指将实体聚集在一起的单元
• 项目集（itemset）：指出现在数据集中的一个或多个事件、实体、数据对象、项的集合

Transactions	Items
1	a, b, c, d
2	b, d
3	b, e
4	a, c, d
5	a, d
6	a, c, e
7	b, c
8	c, e
9	d, e
10	a, c

例如，在情况2中，我们有三个不同的项集：
{b}，{d}，{b，d}。
在情形6，我们有七个不同的项集：
{a}，{c}，{e}，{a，c}，{a，e}，{c，e}，{a，c，e}。

• 数学支持A与B可以被写成
  $$support(A,B)=P(A\cap B)$$
• 置信度（Confidence）：指如果实体A发生，那么实体B也发生的一种值。
  我们可以这么写
  $$confidence(A=>B)=P(A|B)=\frac{support(A,B)}{support(A)}$$

例证

从上表分析可知：
$$support(A,B)=0.1$$
置信度为：
$$confidence(A=>B)=P(A|B)=\frac{0.1}{0.5}=0.2$$

搜索优化算法（ Search Optimization Algorithms）

频繁项集中的挖掘搜索

关联规则挖掘包括两个主要步骤：
第一步：找到频繁项集（或候选项生成）
第二步：生成从频繁项集关联规则（或计算支持和每个候选项的置信度）
其中，大多数时间复杂度高的算法都是为了完成第一步。需要注意的是，如果不使用搜索优化算法，那么数据的时间复杂度将是$O（2^n)$,这意味着即使是在小范围的数据集中，暴力完成的方法也是不可取的。

搜索优化算法

我这里仅列出对应的优化算法，并引用部分csdn优质博客链接供参考
希望大家多多给这些博客博主点赞

• 哈希散列表（Hash Tables）
  哈希散列表
  MinHashing
• 树结构（Tree Structures）
  二叉树
  平衡二叉树
  漫画讲述B-树
  红黑树
  前缀树
• 位操作（Bit Manipulations）
  信息论编码压缩
  LZ压缩
  哈夫曼编码
• 滑动窗算法（Sliding Window）
  Sliding window
• 布隆过滤器（Bloom Filter）
  布隆过滤器
  那我现在假设上面的内容你们都已经有所了解或是掌握，毕竟这是个科普类的博客，我们继续往下。

频繁项集挖掘

算法

• Apriori
  简介：
  Apriori是第一个基于自底向上的关联规则挖掘算法，它迭代地扫描着数据集。在每次迭代中，算法构建两个列表，一个候选列表和一个频繁列表，令其大小为k（kitemset）。随后，再下一次迭代中，算法增加k的大小，并更新候选列表与频繁列表。重复此过程直到常用列表中均不大于最小支持集。然后，满足最小支持条件的频繁项集将被分开，用于计算他们的置信度和最小项集，同时满足最低支持和最小置信度的将被作为频繁项集的结果返回。
  min_support = 0.6 min_confidence=0.8

Txn#	Items
1	a, c, d
2	b, c, e
3	a, b, c, e
4	b, e
5	a, c, e

C1

Itemset	support
a	3
b	3
c	4
d	1
e	4

其中，d < min_support,我们得到
F1

Itemset	support
a	3
b	3
c	4
e	4

使用F1生成C2数据集并对他们进行计数
C2

Itemset	support
a ,b	1
a,c	3
a,e	2
b,c	2
b,e	3
c,e	3

同理，{a,b},{a,e},{b,c}<min_support
我们得到F2
F2

Itemset	support
a,c	3
b,e	3
c,e	3

使用F2生成C3数据集并对他们进行计数
C3

Itemset	support
a,b,c	1
a,b,e	1
a,c,e	2
b,c,e	2

发现所有的都小于min_support，因此F3不存在，退回到F2，作为频繁项集返回。

计算置信度：

置信度是一个值，表示如果一个实体发生，则另一个实体也同时出现。
$$confidence(A=>B)=P(A|B)=\frac{support(A,B)}{support(A)}$$
同样是上面的表格，我们计算可知：
$$\begin{gathered} confidence(a,c)=3/3=1.00 \\ confidence(c,a)=3/4=0.75 \\ confidence(b,e)=3/3=1.00 \\ confidence(e,b)=3/4=0.75 \\ confidence(c,e)=3/4=0.75 \\ confidence(e,c)=3/4=0.75 \end{gathered}$$
据上述结果可知，最小频繁集为{a，c}，{b，e}，因为其余的都小于最小置信度（0.8）
code：

pip install efficient_apriori
from efficient_apriori import apriori
transactions = [('eggs', 'bread', 'soup'),
 ('eggs', 'bread', 'apple'),
 ('soup', 'bread', 'banana'),
 ('bread','banana','jam')]
# note support and confidence should be between 0 and 1
itemsets, rules = apriori(transactions, min_support=0.5,
min_confidence=0.8)
print(rules) 
复制

• FP-Growth
• 简介
  Apriori在数据集大小增长时并不有效，因为：
  （i）它需要创建一个非常大的候选列表。
  （ii）它需要的在每个迭代中扫描数据集以生成频繁项集列表。
  FP-Growth算法分为两个主要步骤：
  （i）创建FP-Tree（频繁模式树，是一个压缩的树中数据集）
  （ii）分割压缩数据集（FP-Tree）成一组更小的数据集。这些小数据集叫做条件模式基于，FP-Growth算法从中寻找频繁项集
  演示如下：
  
  （a） 包含八个事务的样本数据集
  （b）已计算每个项目的支持度
  （c）已删除低于最小支持的项目
  然后，该算法扫描原始数据集中的每个事务，并根据支持的频率对其项进行排序，并得到下表：

Txn#	Items	based on min_support
1	a, c, d, e	e, d, a, c
2	a, b, d	d, a
3	c, d, e	e, d, c
4	a, b, c, e	e, a, c
5	b, d, e	e, d
6	a, d, e	e, d, a
7	a, c , d	d, a
8	b, d, e	e,d

min_support=3

相较于原数据集，FP树显然占用更少的空间，因为有些项集共享了部分路径
，同时FP树也包含了我们所需要的所有数据。
下一步就是从FP树中提取条件模式.该算法采用自底向上的方法，即从叶节点开始到根节点,按照以下顺序{c，a，d，e}.

• 我们需要看看“c”是否是基于给定最小支持的频繁项集：该算法计算子树中的“c”（沿虚线计算“c”的所有值），其中有3个“c”小于最小支持，因此子树2将被解析。第二层子树是“a”。如图，满足最小支撑条件。因此，它列出了结尾有“a”的频繁项集，如下所示：
  {e，d，a}，{d，a}，{e，a}
  同理我们列出d、e的{d,e},{d},{e}

• 创建“条件模式库”之后，下一步是创建“条件FP树”，该算法通过“条件基模式”并选择所有“条件模式库”中共同的项目。
  对于’c’，其条件模式基唯一常见项时e，且出现了三次，即{e:3}

• 在创建了条件FP-Tree之后，下一步是创建频繁模式，如“frequent pattern”列中所示,您可以在下面看到，通过将项“d”组合到它的“条件FP树”，我们将得到一个频繁模式：{d，e:5}
  
  a，d 小于最小支持，直接略过
  计算置信度：
  $$\begin{gathered} confidence(d,e)=5/6=0.83 \\ confidence(e,d)=0 \\ confidence(c,e)=3/4=0.75 \\ confidence(e,c)=0 \\ confidence(a,e)=3/5=0.6 \\ confidence(e,a)=3/6=0.5 \\ confidence(a,d)=3/7=0.42 \\ confidence(d,a)=3/5=0.6 \end{gathered}$$
  {d，e}，{c，e}，{a，e}，{e，a}，{e，a},{d，a}可以作为关联规则返回.

code：

import pyfpgrowth
transactions = [('eggs', 'bread', 'soup'),
 ('eggs', 'bread', 'apple'),
 ('soup', 'bread', 'banana'),
 ('bread','banana','jam')]
patterns = pyfpgrowth.find_frequent_patterns(transactions, 2)
patterns
复制

• Eclat
  等价类转换（ECLAT）是一种频繁关联挖掘算法，它不像Apriori需要频繁扫描数据集。
  Eclat假定事务按字典顺序排序，它处理每个项目的支持标识过程与一般的方法有所不同。Eclat在DFS模式下搜索项目树，DFS可以更快地发现长频模式，但这对于存储来说通常不是有效方案。
  Eclat将数据集转换为垂直格式并扫描tid列表数据集,然后根据tid列表之间的交集，提取频繁模式。在创建tid列表之后，该算法迭代新生成的tid列表，并比较每个项目tid列表与所有其他tid列表的交集。换言之，在第k个频繁项集被识别后，该算法将k增加到k+1，并在最新项列表上再次迭代以识别频繁项集（基于项的tid列表之间的交集）。
  重复此过程，直到不再有交集，并且所有交集结果将为空或小于最小支持。
  

code：

import pandas as pd
from fim import eclat
transactions = [('eggs', 'bread', 'soup'),
 ('eggs', 'bread', 'apple'),
 ('soup', 'bread', 'banana'),
 (‘bread','banana','jam')]
rules = eclat(tracts = transactions, zmin = 3)
rules
复制

频繁项集挖掘

关联规则挖掘算法没有考虑事务中数据对象的顺序。他们希望用户通过词典对条目进行排序，然后将它们输入到算法中。当数据顺序较为重要是，关联规则挖掘的弊端就出现了，比如，包含时间戳或具有时间概念及其事件时间的数据集。
事务内容将定义为<a，b，（c，d），f>格式。这意味着第一个事件是’a’，然后是’b’，接着’c’和’d’（同时发生），最后’f’发生。

• GSP
  广义序列模式算法[Srikant’96]（GSP）是一种基本的序列模式挖掘算法。
  第一步（候选生成），计算数据集中每个项的所有支持。
  第二步（修剪），删除频率小于最小支持的元素。
  第三步，合并项目并创建k+1大小元素序列（k是迭代次数）。
  重复执行第二步和第三步，直到没有新的项集将被创建。
  
  
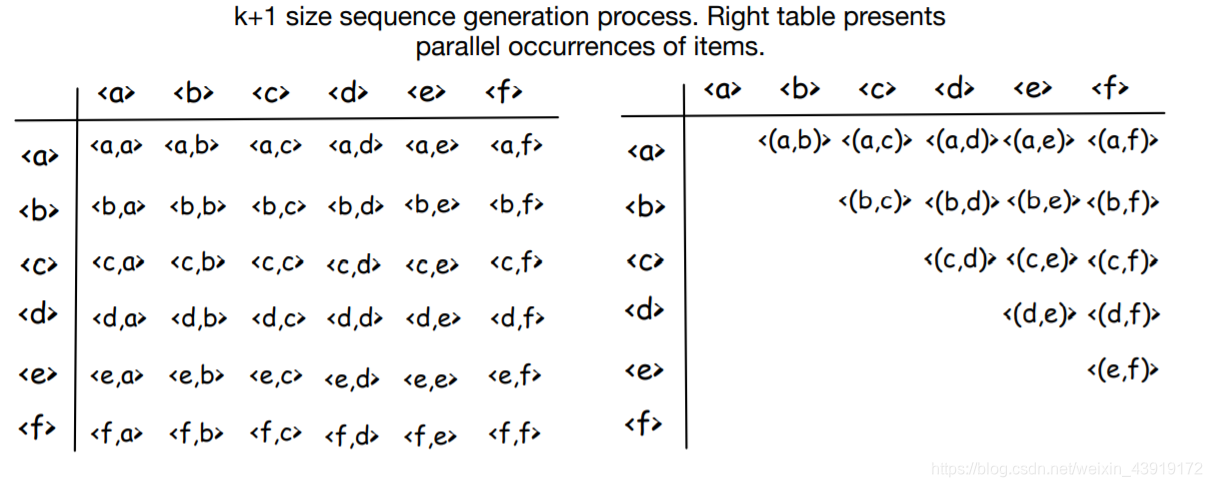
  通过检查两个表中的所有元素。我们将有以下序列：
  $<a，a>，<a，b>，<a，c>，<a，d>，<a，e>，<a，f>，\dots <f，f>，<（a，b）>\dots <（e，f）>$
  然后统计数据集中的这些序列，并删除那些小于min_support的序列。例如$<a，a>$存在于Seq ID.3和Seq ID.5中，保留; $<a，f>$只存在于Seq ID.3中，因此它的出现次数小于min_support=2，移除。
  同样，该算法增加迭代值（k=2）并执行另一个迭代，产生以下序列：
  $<a，a，a>，<a，a，b>，<a，a，c>，<a，a，d>，\dots <f，f，f>，<（a，b），a>\dots ，<（e，f），f>$，重复此过程，直到没有支持度等于或大于min_支持度的序列，然后算法结束并返回频繁序列，例如$<（x2，x4），x3，x2，x1>$（在数据集的第五次扫描中获得）和$<x1，x2，x2，x1>，<（x2，x4），x2，x3>$，…在数据集的第四次扫描中获得。

• SPADE
  SPADE（stays for Sequential Pattern Discovery）使用的等效类是一种以垂直数据格式运行的序列模式挖掘算法。
  首先，它对数据集执行一次扫描，并将数据从水平格式映射到垂直格式。然后，通过连接（k-1）序列的ID来识别k序列。将水平数据集转换为垂直数据集，然后根据其SID和EID分离每个元素:
  
  
  我们可以看到表’c’、‘e’、‘g’、‘f’和’h’小于min_支持，因此它们将被删除，接下来，算法根据元素表创建元素的组合。这意味着我们还有a，b，d和f，那么算法应该构造它们的二阶组合，即aa，ab，ad，af…
  现在，它把这些小表合并成一个组合表。这个组合是基于（i）等SID和（ii）元素的数字顺序构建的。例如，考虑构建AA。
  第一个元素是“2”。然后将其与“2”进行比较，由于两者相等，因此算法不会将它们写入结果表（检查下表中的红点和红线）。注意，条件是：第一个EID应该小于第二个EID。
  接下来，算法移动到下一个元素，现在它打算将2与3进行比较，2<3因此可以将它们添加到aa表中（见下表中的蓝色虚线）。
  
  
  为了构造三个元素的组合，该算法将相关的三个表的内容连接起来。
  例如，aab将由“a”、“b”和“a”之间的联接构造。abf将由’a’、'b’和’f’之间的连接来解释。下表提供了四个关于算法如何构造三元素联合表的示例。
  从结果来看，只有两个元素列为频繁序列似乎很奇怪，不过，我们应该记住括号内的事件不是以一个序列发生的，而是以并行的方式发生的，因此算法正确地没有将括号中的内容视为一个序列。
  

• code

data(zaki)
inspect(zaki)
## mine frequent sequences
s1 <- cspade(zaki, parameter = list(support = 0.4),
control=list(verbose = TRUE, tidLists = TRUE))
#s1 <- cspade(zaki, parameter = list(support = 0.4))
summary(s1)
as(s1, "data.frame")
##
summary(tidLists(s1))
transactionInfo(tidLists(s1))
复制

SPADE和GSP都非常有用，但它们有三个缺点：
（i）对数据集执行多次扫描，复杂度高
（ii）生成非常大的候选列表，空间复杂度大
（iii）且不是挖掘长序列模式的最佳方法（与Apriori问题非常相似）。
有一些更nb的算法可以减少数据集扫描，比如FreeSpan和PrefixSpan。

• FreeSpan
  FreeSpan是“frequent pattern-projected sequential pattern mining”,它基于“模式增长”的概念运作。
  模式增长不需要频繁的候选生成，它递归地创建“投影数据集”，将它们的搜索空间减少到更小的分区中。投影数据集是指从原始数据集递归派生的较小大小的数据集。在从原始数据集派生投影数据集时，频繁项集（序列模式）已经是投影数据集的已知内容。从第一个数据集（不包括第一个数据集）中递归地创建其他数据集的非频繁数据集。
  因此，算法最终得到每个投影数据集中的序列模式列表。
  
  因此，该算法最终得到每个投影数据集中的序列模式列表“a”投影数据集是$<a，a，a>，<a>，<a>，<a>$。为了了解我们是如何做到这一点的，让我们看看下表。然后，该算法从投影数据集中提取序列模式，即“$<a，a>：2，<a>：2$”。所以我们可以说，从数据集$<a，a，a>，<a>，<a>，<a>$，提取了序列模式$<aa>$和$<a>$
  
  
  
  “b”投影数据集是{<a，（ba），a>，<a，b，a>，<（ab），b>，<a，b>}。分析下表，通过搜索这个数据集，我们得到了四个新的序列模式：$<a，b>：4，<b，a>：4，<（ab）>：2，<aba>：2$
  
  
  “c”投影数据集是$<a，（abc），（ac），c>，<a，c，（bc），（ac）>，<（ab），c，b>，<a，c，b，c>$该算法识别频繁的序列模式，
  如下所示。具体来说，算法首先识别长度为2的序列模式，‘c’的投影数据集：$<a，c>：4，<（bc）>：2，<b，c>：3，<c，c>：3，<c，a>：2，<c，b>：3$
  
  为了识别长度为3的序列模式，对每个识别模式创建另一个投影数据集。
  例如
  $<a，c>$投影集=$<a，（abc），（ac），c>，<a，c，（bc），a>，<（ab），c，b>，<a，c，b，c>$
  这个递归循环一直持续到没有序列模式可识别为止。例如，从<a，c>-投影数据集中，我们有$<a，c，b>：3，<a，c，c>：3，<（ab），c>：2，<a，c，a>：2$从$<a，c>$投影的数据集中识别出的序列模式，但是如果我们寻找$⟨a，c，b⟩$投影数据集，$<a，c，c>$-投影数据集等。将没有4长度的序列模式，递归循环中断。

• PrefixSpan
  频繁模式投影序列模式挖掘（PrefixSpan使用数据集的投影序列（将搜索空间划分为更小的数据集）来减少搜索空间。它类似于FreeSpan，但不是从所有可能的频繁子序列创建投影序列数据集，而是基于前缀创建投影数据集。
  前缀是序列开头的一个项，后缀是序列的剩余部分（没有前缀）。
  例如：$<a，（abc），（ac），d，（cf）>$，我们可以提取其后缀和前缀如下：
  Prefix：$<a>$Suffix：$<（abc）（ac），d，（cf）>$
  Prefix：$<aa>$Suffix：$<（bc）（ac），d，（cf）>$
  Prefix：$<ab>$Suffix：$<（c）（ac），d，（cf）>$
  接着将搜索空间划分为更小的数据集，并为每个前缀创建一个投影数据集。
  （1） 仅包含“a”的项的子集
  （2） 包含“b”但不包含“b”之后的项的子集，即仅“a”和“b”
  （3） 包含“c”但不包含“c”之后的项的子集，即“a”、“b”和“c”
  （4） 包含“d”但不包含“d”之后的项的子集
  （5） 包含“e”但不包含“e”之后的项的子集
  （6） 仅包含“f”的项的子集
  
  注：在对数据集进行一次扫描时，所有这六个投影数据集将被构造一次。此外，在将数据集投影到后缀数据集时，前缀项之前的每一项（忽略它们的顺序）都将被删除。
  
  最后是在这些数据集中找到顺序模式。然后，增加前缀的长度(例如，prefix$<a>$变为prefix$<af>$和$prefix<aa>$)，并在新数据集中找到长度更长的序列模式。持续这个过程直到没有候选频繁序列被生成。
  

• ** code**

from prefixspan import PrefixSpan
db = [
 ['a', 'b', 'c', 'd', 'e'],
 ['b', 'b', 'b', 'd', 'e'],
 ['c', 'b', 'c', 'c', 'a'],
 ['b', 'b', 'b', 'c', 'c'],
]
ps = PrefixSpan(db)
print(ps.frequent(4))
print("-----------")
print(ps.frequent(3))
print("-----------")
print(ps.frequent(2))
复制

好了，水完了，不点个赞再走嘛

不点赞给我介绍个女朋友也行啊