约瑟夫问题_公式原理详解

小-黯

37501人浏览 · 2020-04-14 21:54:34

小-黯 · 2020-04-14 21:54:34 发布

一、约瑟夫问题：

在计算机编程的算法中，类似问题又称为约瑟夫环
约瑟夫环：N个人围成一圈，从第一个开始报数，第M个将被杀掉，最后剩下一个，其余人都将被杀掉。
例如N=6，M=5，被杀掉的顺序是：5，4，6，2，3，1。
如图：

二、公式原理

同例：N个人围成一圈，从第一个开始从1报数，第M个将被杀掉，最后剩下一个，其余人都将被杀掉。

如果我们从N个人开始一个一个的将被杀死的取出，我们要不断的循环遍历约瑟夫环，时间复杂度高达O（M*N）

假设我们反向推导，从只有一个人参与这个游戏开始，递推出N个人参加游戏的结果，就会变得简单多了，推导原理如下：

总人数：1人
	F（1,5）=0，假设存活人的序号为x
	排序顺序：x【0】

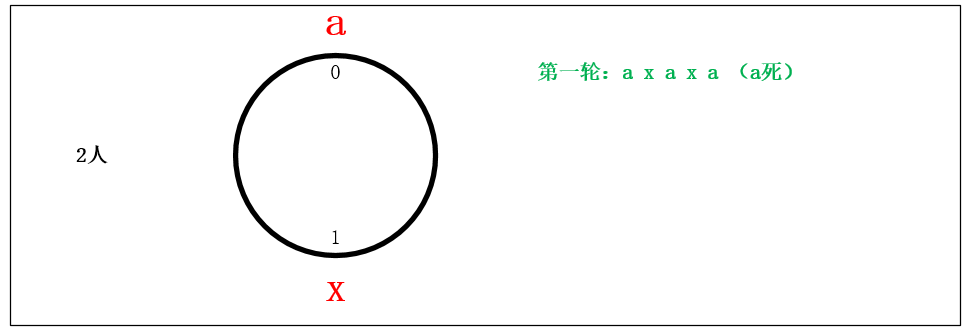
总人数：2人
	假设另外一个被杀的人的序号是a，则报数顺序是可以直接确定的
	条件：
		一死一活，已知x号是存活者，则第一次报第五个数的人必死
	
	报数顺序：a x a x a 
	排序位置：a[0] x[1]	(每次从0开始报数）
	
	！x的位置 = 总人数为1时的位置向后数5个数 = （0 + 5）% 2 = 1

在这里插入图片描述

总人数：3人
	假设第二位被杀的人的序号是b，则报数顺序依然确定
	俩个条件确定顺序：
		1、第一次报第五个数的人一定是b
		2、b死后总人数为2的排序已知
	
	报数顺序：x b a x b
	排序位置：x[0] b[1] a[2]
	
	！x的位置 = 总人数为2时的位置向后数5个数 =（1 + 5）% 3 = 0
	！a的位置 = 总人数为2时的位置向后数5个数 =（0 + 5）% 3 = 2

在这里插入图片描述

总人数：4人
	假设第三位被杀的人的序号是c，同理可确定报数顺序
	
	报数顺序：c x b a c
	排序位置：c[0] x[1] b[2] a[3]
	
	！x的位置 = 总人数为3时的位置向后数5个数 =（0 + 5）% 4 = 1
	！a的位置 = 总人数为3时的位置向后数5个数 =（2 + 5）% 4 = 3
	！b的位置 = 总人数为3时的位置向后数5个数 =（1 + 5）% 4 = 2

在这里插入图片描述

总人数：5人
	假设第四位被杀的人的序号是d，同理可确定报数顺序
	
	报数顺序：c a b x d
	排序位置：c[0] x[1] b[2] a[3] d[4]
	
	！x的位置 = 总人数为4时的位置向后数5个数 =（1 + 5）% 5 = 1
	！a的位置 = 总人数为4时的位置向后数5个数 =（3 + 5）% 5 = 3
	！b的位置 = 总人数为4时的位置向后数5个数 =（2 + 5）% 5 = 2
	！c的位置 = 总人数为4时的位置向后数5个数 =（0 + 5）% 5 = 0

在这里插入图片描述

总人数：6人
	假设第五位被杀的人的序号是e，同理可确定报数顺序
	报数顺序：c a b x e
	排序位置：x[0] b[1] a[2] d[3] e[4] c[5]
	
	！x的位置 = 总人数为5时的位置向后数5个数 =（1 + 5）% 6 = 0
	！a的位置 = 总人数为5时的位置向后数5个数 =（3 + 5）% 6 = 2
	！b的位置 = 总人数为5时的位置向后数5个数 =（2 + 5）% 6 = 1
	！c的位置 = 总人数为5时的位置向后数5个数 =（0 + 5）% 6 = 5
	！d的位置 = 总人数为5时的位置向后数5个数 =（4 + 5）% 6 = 3

在这里插入图片描述
由此我们可以总结出规律

每次增加一个人，我们第一轮的报数被指定的必定是新加入的人
例如当人数从5个增加到6个的过程如下：

三、公式递推

假设：
存活者位置 = F（N，M）；

例如N=6，M=5，被杀掉的顺序是：5，4，6，2，3，1。可知：
存活者位置 = F（6，5）；

给出例子中求存活者位置的递推过程
总人数 = 1 ： F（1，5）= 0
总人数 = 2 ： F（2，5）= （F（1，5）+5）% 2 = 1
总人数 = 3 ： F（3，5）= （F（2，5）+5）% 3 = 0
总人数 = 4 ： F（4，5）= （F（3，5）+5）% 4 = 1
总人数 = 5 ： F（5，5）= （F（4，5）+5）% 5 = 1
总人数 = 6 ： F（6，5）= （F（5，5）+5）% 6 = 0

思考：为什么加5取余？

例：F（3，5）= （F（2，5）+5）% 3 = 0

此时总共3人，即[0] 、[1]、[2]三个位置
在原本只有两个人的情况下，存活位置为【1】的人需要向后移动五个单位
而要向后数五个单位，则需要以环形的结构进行遍历
->[2]->[0]->[1]->[2]->[0]
也就是环形遍历约瑟夫环，得出最后停在[0]的位置，这也是取3的余数得出的结果。

最后我们得出公式

F（N，M）=（F（N-1，M）+M）%N

C语言代码

#include<stdio.h>
int main()
{
	int n,m;
	while(scanf("%d %d",&n,&m)!=-1)
	{
		int p=0;
		for(int i=2;i<=n;i++)
			p=(p+m)%i;
		printf("%d\n",p+1);
	}
	return 0;
}