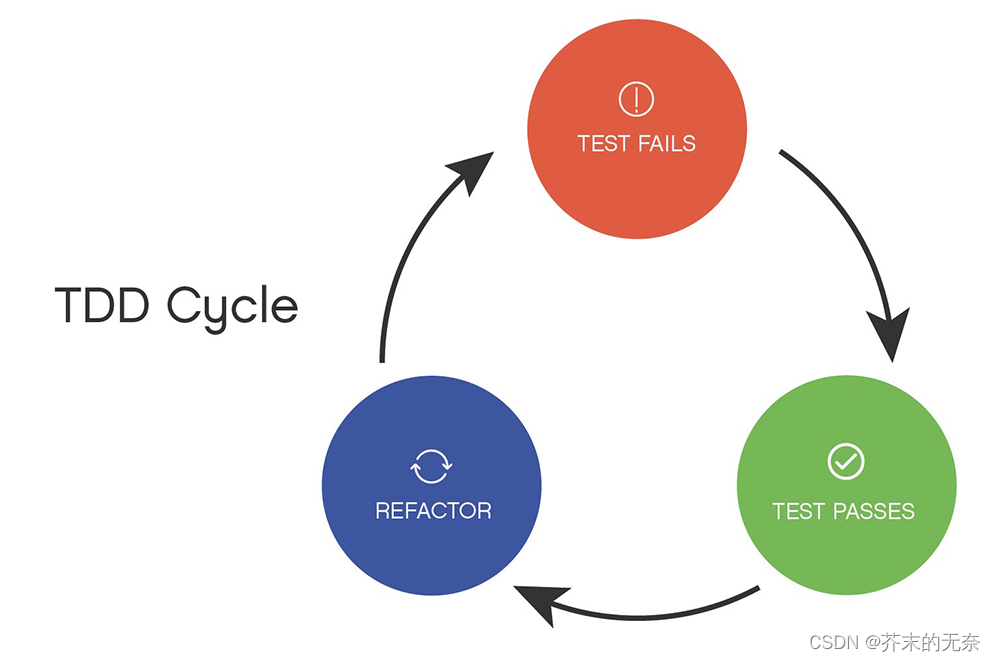
引言测试驱动开发，英文全称 Test-Driven Development，简称 TDD，是一种不同于传统软件开发流程的开发方法。在《程序员的职业素养》第五章，我第一次看到有关 TDD 内容，当时Bob大叔向我展示了一种不可思议的编程开发方法，这种方法颠覆了我的认知。Bob 大叔列举了 TDD 很多好处，例如确定性、降低代码缺陷、方便代码重构、测试单元文档化，更优秀的代码设计等等。并强力安利读者们

机器学习(深度学习)通用工作流程翻译 Deep Learning with Python 4.5节1. 定义问题并装载数据集(Defining the problem and assembling a dataset)首先，你必须定义你手头的问题：输入数据是什么？你希望预测什么？只有在能够获得训练数据的情况下你才能进行预测：举个例子，如果你同时又电影的影评和对应的情感注释，你

本章讨论 OpenGL ES 中多线程技术的运用。首先，说明我们为什么需要这项技术，在 ARM OpenGL ES 教程中提到当我们转向更复杂的图形应用程序时，可能会想要使用多线程（MT）。一个典型的情况是，我们的图形应用程序需要执行大量的数学运算。在这种情况下，可能通过将工作量移至不同于管理图形操作的线程来提高性能。另一个常见的例子是我们想让图形用户界面（GUI）在一个独立的线程中运行。多线程的

介绍了一种分析时间序列的方法 Matrix Profile，具有简单性、易用性、普适性等优点，另外介绍了MP的具体应用，展示了如何利用MP去分析时间序列。

Karplus-Strong 算法简单介绍和实现本文为Coursera数字信号处理课程第一周内容，对相关课程刚兴趣的同学，请参看这里为了有更好的交互性，本文所有代码均上传至Microsoft Azure Notebooks，你可以在上面试听所有输出的音频，具体代码在这里什么是Karplus-Strong算法Karplus-Strong算法简单的说就是一种合成声音的算法，它不断的循环重复...

DFTDFT(Discrete Fourier Transform)，离散傅里叶变化，可以将离散信号变换到频域，它的公式非常简单:X[k]=∑n=0N−1x[n]e−j2πkn/NX[k] = \sum_{n=0}^{N-1} x[n] e^{-j2\pi kn/N}X[k]=n=0∑N−1​x[n]e−j2πkn/NX[k]X[k]X[k]：离散频率下标为k时的频率大小x[n]x[n...

系列文章目录【音频处理】如何“认识”一个滤波器？【音频处理】IIR滤波器设计（一）【音频处理】IIR滤波器设计（二）文章目录系列文章目录前言一、模拟信号滤波器到数字信号滤波器的转换1. S域与Z域2. 模拟信号滤波器3. 双线性变换二前言在 【音频处理】IIR滤波器设计（一） 中，我们介绍了多种滤波器，并给出它们的差分方程、变换方程等。针对每种滤波器，我们都举了一个具体的实例来说明。同时，还讨论了

BP神经网络简单介绍在60年代提出了神经网络概念之后，由于感知机等神经网络无法处理线性不可分问题（比如异或问题）导致人们对神经网络的兴趣大减，认为神经网络的能力有限，只能处理线性可分问题。之后，有人提出了多层神经网络的想法，用于解决异或问题。下面就是用一个两层的神经网络解决异或问题具体方法：y=ψ(−2v1+v2−0.5)v1=ψ(x1+x2−1.5)v2=ψ(x1+x2−0.5)ψ(x)={1

文章目录傅里叶变换的基本性质线性性质平移性质对称性质卷积性质傅里叶变换的基本性质总的来说，傅里叶变换有这样几个性质：线性性质（Linearity）平移性质（Shift）对称性质（Symmetry）卷积性质（Convolution）参考 傅里叶变换-wikipedia线性性质线性性质：两个函数之和的傅里叶变换等于各自变换之和，反之亦然import numpy as npf...

本章内容是对 GStreamer 官方教程中第九、十和十一三章的一个介绍。这几章涉及的代码不多，主要是介绍 GStreamer 中工具，包括 GstDiscoverer、gst-discoverer-1.0、gst-launch-1.0、gst-inspect-1.0 、日志工具等。这块可以扩展的内容比较少，但我又不想漏了这块，因此本文只是做一些粗粒度的总结。