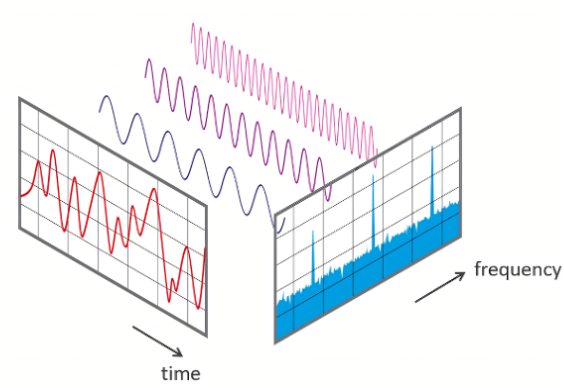
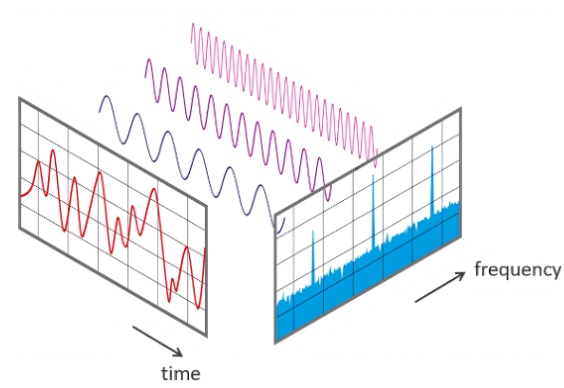
频率的估算是通过查找信号中的峰值并计算相邻峰值之间的平均时间差来实现的。幅值的估算是通过信号的最大值和最小值来计算的。相位的估算是通过第一个峰值的值和幅值来实现的。

莎士比亚说过：“有一千个读者就有一千个哈姆雷特”，对于FFT，每个人的理解，小编相信都是不一样的，但是不得不说书上关于FFT的说明，小编真的看不明白，理解较为困难。以下是小编自己的一些想法，FFT真正有自己的理解有点难，这里建议大家可以多看看他人关于FFT的分析与解释，总有一种是适合你的理解。一整个苹果就相当于我们所给的原始信号，而FFT的作用就是将苹果的营养成分表列出来，让我们知道苹果是由哪些营

史上最全SCI论文配图代码

一般来说，FFT的数据点个数为以2为基数的整数次方（采用以2为基的FFT算法，可以提升运算性能），但是并没有要求FFT的数据点个数一定为2的n次方。），大于1 MHz 和1.05 MHz之间距离的50kHz，且波形分辨率只与原始数据的时长T有关，与参与FFT的数据点数无关，因此补多少零都无用。存在，而在1.05MHz处却没有，使得测量结果偏离实际值，同时在实际频率点的能量分散在两侧的其他频率点上，

1.通常，在声学中，波数的计算公式取决于介质的性质和声波的频率。在空气或类似的介质中，波数通常与声速和频率相关，计算公式如下：对于空气中的声速，常温下约为 343 m/s，因此可以用这个值来进行计算。如果您有频率值，则可以直接使用该公式计算波数。如果需要考虑材料的吸声或衰减效应，波数可能是复数形式。此时，波数可以表示为：复波数的虚部（衰减系数）通常与材料的吸声特性（如吸声系数）和频率相关。2.

可以看到，在低频和高频区域，为了达到相同的响度，需要更高的声压级，而在中频区域（特别是1kHz附近），较低的声压级就能达到相同的响度。声音信号的响度是指人耳对声音强度的主观感受，它与声音的声压级（Sound Pressure Level, SPL）有关，但并不是直接等同于物理上的声压级。例如，在1kHz频率下，40分贝的声压级和在100Hz频率下约60分贝的声压级听起来一样响。中频（约1kHz至5

1、采样频率的计算通过时间数据计算采样频率。：从 CSV 文件中读取的时间列，：计算时间数据中每个连续点之间的时间差，：取所有时间差的平均值，得到采样周期采样频率：是采样周期的倒数，表示每秒采集多少个数据点，单位是（赫兹）。2.上述代码完全诠释了采样点数与FFT变换点数之间的关系。：原始电压数据的长度: 返回使的最小整数: 用于 FFT 的变换点数，保证为 2 的幂次方为了保证 FFT 计算的高效

根据不同的标准，主动噪声控制（ANC）系统可以进行多种划分，每种分类都有其应用场景和优缺点。除了常见的按控制信号获取方式、误差传声器数量、频谱特征等方式划分外，还可以根据噪声源的分布、控制方式以及系统复杂度等因素进一步细分。

是信号处理和控制领域中的重要技术，用于以，从而优化滤波器性能。按实现原理分类，可分为线性与非线性。线性自适应滤波算法：假设滤波器的输入输出关系是线性的；适用于线性信号和系统环境。非线性自适应滤波算法：适用于具有非线性特性的信号或系统；通过增加非线性映射或结构，处理复杂的信号模式。①线性自适应滤波算法NLMS 是 LMS 的改进版本，旨在解决 LMS 算法中因输入信号幅值变化较大而导致的收敛性问题。

多孔材料的声学理论模型是用于描述和预测声波在多孔介质（如海绵、泡沫、隔音材料等）中传播和行为的数学和物理模型。这些模型帮助我们理解声波如何与多孔材料相互作用，包括声波的传播、吸收、反射和衰减等现象。声速和声阻抗：模型可以计算声波在多孔材料中的传播速度和声阻抗，这些参数影响声波的传播特性。声场分布：分析声波在多孔材料中的分布和变化，包括声压和声强度。吸声性能：模型用于预测多孔材料的吸声系数，即材料对