三种颜色模式的H都是指色彩（Hue），S指饱和度（Saturation）；HSB/HSV/HSL中的B/V/L都指亮度，分别为英文单词Brightness/Value/Lightness;三种颜色模式都能通过RGB模式由数学公式转化而来，那么问题来了，既然有了RGB模式，为啥还要其它模式呢？RGB对机器更友好，但R,G,B三个干硬数字对人来说不够直观，HSB/HSV/HSL的设计对人更友好，先..

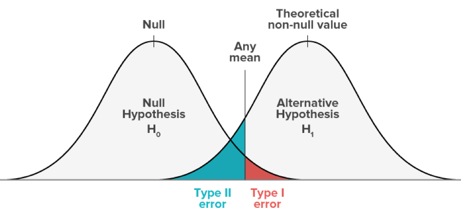
1，type 1 error对应假阳性率，type 2 error对应假阴性率。Reality如果零假设正确，那么现在根据Research零假设进行推断； Research如果观察值落在红色区域左边，那么就会接受零假设，与Reality相符，正确的概率为1-α；反之， Research如果观察值落在红色区域内，那么就会拒绝零假设，这时候的拒绝是错误的，这个错误就是type I error。Re..

1，在直角坐标系中，某个点是一个方向上的极大值，另一个方向上的极小值，则该点是鞍点。对于二维平面，如y=x3y=x^3y=x3在x=0处，该点又称为驻点。对于三维平面，如y=x2−y2y=x^2-y^2y=x2−y2在（0，0，0）处就是一个鞍点。2，在微分方程中，沿着某一方向是稳定的，沿着另一方向不稳定的奇点，就叫鞍点；在泛函分析中，既不是极大值点也不是极小值低点的临界点就叫做鞍点；在矩阵...

1，用于复合函数求导的一个法则。2，应用场景：假设要对y=f(g(x))求导，即求dydx的值，假设要对y=f(g(x))求导，即求\frac{dy}{dx}的值，假设要对y=f(g(x))求导，即求dxdy​的值，可以设μ=g(x),可以设\mu=g(x),可以设μ=g(x),则dydx=dydμ×dμdx则\frac{dy}{dx}=\frac{dy}{d\mu}\times\frac...

药物处理细胞后会通过一系列指标对细胞的敏感性进行评估，主要有一下几个方面：Area Under the Curve (AUC)Half maximal inhibitory concentration (IC50)The concentration where the fitted curve crosses 50% in cell viabilityHalf maximal effec...

1，最大似然损失函数（Likelihood loss）常用在分类问题上。形式上是把每一个预测值的概率相乘，得到一个损失值。例如：对一组样本的预测为True(1)概率为[0.4, 0.6, 0.9, 0.1]，它们的真实值分别为[0, 1, 1, 0]，则损失值为0.6∗0.6∗0.9∗0.9=0.29160.6*0.6*0.9*0.9=0.29160.6∗0.6∗0.9∗0.9=0.2916，..

OR值的全称是odds ratio、比值比，对于发病率很低的疾病来说，它是OR值即是相对危险度的精确估计值。OR值的意义：OR值等于1，表示该因素对疾病的发生不起作用；OR值大于1，表示该因素是危险因素；OR值小于1，表示该因素是保护因素。计算公式如下：假定我们要鉴别因素（例如吸烟）是不是某个疾病的危险因素（例如肺癌）。形成如下四个表：吸烟不吸烟肺癌AB正...

1，定义KKT是啥？它是Karush、Kuhn和Tucker三个人。这三个人单独提出了在非线性规划中获得最优解的必要条件。看着很复杂呀？还好啦。。。只是将拉格朗日乘数法中的等式约束条件泛化到了不等式。2，先来几个简单例子为什么要搞这个看似复杂的东东？当然是为了解决一些问题。下面的问题如果你能解出来，你就可以不用学这个了。2.1 求f(x1,x2)=x12+x22的最小值，约束条件为x...

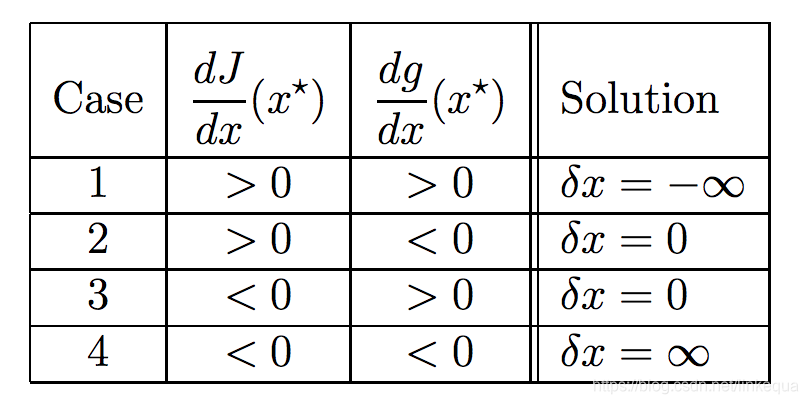
1，补充知识1.1 欧式空间（Euclidean space）直观感受：二维平面，三维立体，拓展到高维空间就对应着超平面。我们在初高中以及大学中的高等数学、线性代数遇到的都是欧几里得空间。为了在数学上准确描述这个空间，需要定义距离、夹角、平移、旋转等概念。两个向量的内积通常会对应到欧几里得平面的一个点。Euclidean plane was defined as a two-dimensi...

1，两条线平行，它们的斜率肯定相同，首先将x和有前面的系数化为相同，设为a和b。则两条直线方程分别为：Line 1: ax1 + by1 + c1 = 0Line 2: ax2 +by2 + c2 = 0d(Line1,Line2)=∣c1−c2∣/a2+b2d(Line 1, Line2)=|c1-c2|/\sqrt{a^2+b^2}d(Line1,Line2)=∣c1−c2∣/a2+b...