之前说了泰勒公式的来历，我们这里继续说下如何直观理解泰勒公式的代数形式，以及泰勒公式最重要的收敛半径。1 泰勒公式的代数形式1.1 定义从泰勒公式的定义开始吧：设是一个正整数。如果定义在一个包含的区间上的函数在点处次可导，那么对于这个区间上的任意都有：，其中的多项式称为函数在处的泰勒展开式，是泰勒公式的余项且是的高阶无穷小。----维基百科泰勒公式的定义看起来气势磅礴，高端大气。如果的话，就是麦克

从数学上讲，卷积就是一种运算。某种运算，能被定义出来，至少有以下特征：首先是抽象的、符号化的其次，在生活、科研中，有着广泛的作用比如加法： ，是抽象的，本身只是一个数学符号在现实中，有非常多的意义，比如增加、合成、旋转等等卷积，是我们学习高等数学之后，新接触的一种运算，因为涉及到积分、级数，所以看起来觉得很复杂。1 卷积的定义我们称 ...

五次及以上多项式方程没有根式解（就是没有像二次方程那样的万能公式），这个是被伽罗瓦用群论做出的最著名的结论。但是，没有王屠夫难道非得吃带毛猪？工作生活中还是有诸多求解高次方程的真实需求（比如行星的轨道计算，往往就是涉及到很复杂的高次方程），这日子可怎么过下去啊？没有根式解不意味着方程解不出来，数学家也提供了很多方法，牛顿迭代法就是其中一种。1 切线是曲线的线性逼近要讲牛顿迭代法之前...

通过矩阵来研究二次函数（方程），这就是线性代数中二次型的重点。1 二次函数（方程）的特点1.1 二次函数最简单的一元二次函数就是：给它增加一次项不会改变形状：增加常数项就更不用说了，更不会改变形状。1.2 二次方程下面是一个二元二次方程：给它增加一次项也不会改变形状，只是看上去有些伸缩：1.3 小结对于二次函数或者二次方程，二次部分是主要部分...

相似矩阵是线性代数中重要的知识，本文将介绍如何通俗地理解相似矩阵——马同学图解数学

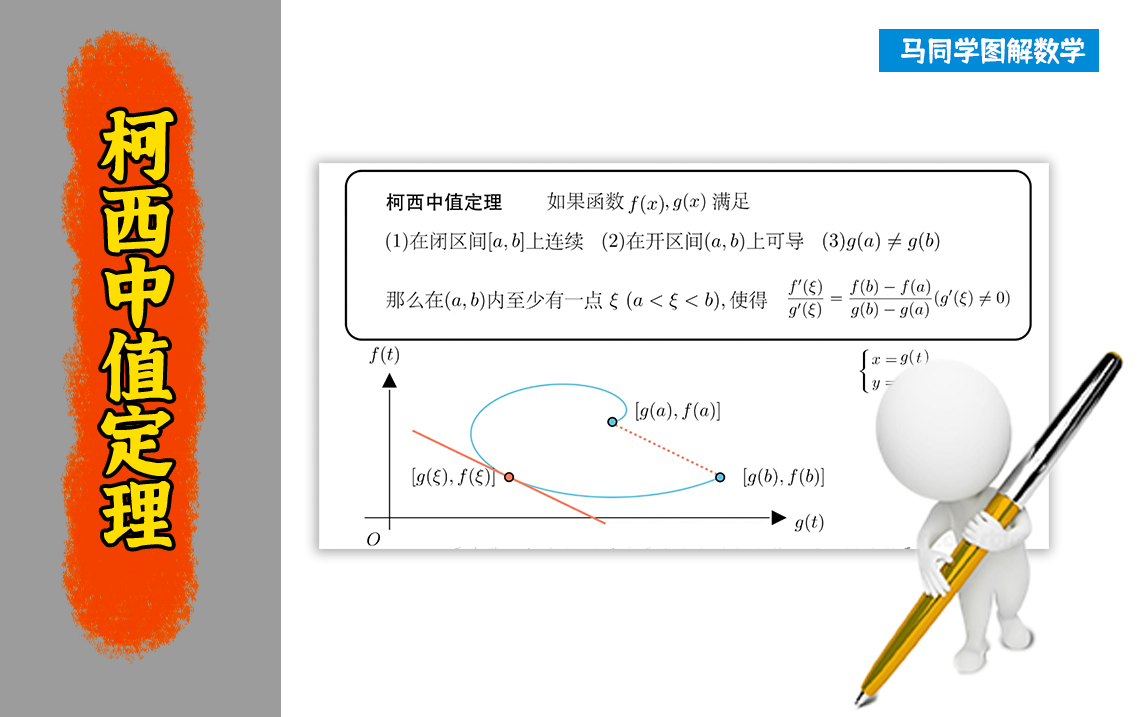
前面说过，拉格朗日中值定理是罗尔中值定理的推广，这在几何上就可以体现。比如下面这条蓝色曲线，因为它能用函数表示，且闭曲间连续，开区间可导。前面我们已经学习了罗尔中值定理,和拉格朗日中值定理，它们的相同点是，研究的曲线都能用函数来表示。还是这条曲线,固定起点不变,对终点进行拉伸,此时，这条曲线无法再用函数表示，也就不符合拉格朗日中值定理。这样柯西中值定理的结论就是,曲线上至少有一点，它的切线的斜率与

在经济学上，有一个概念是沉没成本，大概指的是已经付出的、且不可收回的成本。针对这个概念有一个常见的说法：这句话的意思是，既然沉没成本不可收回，那么在做选择的时候就不应该考虑它。举一个简单的例子，买票去看电影，放映10分钟你就知道这是一部烂片，那么有两个选项（图片出自沉没成本谬误）：此时这张电影票已经消费了，没有办法收回，购买电影票的钱就是沉没成本。这个时候如果想离开电影院就直接离开...

t检验、t分布、t值其实都是同一个数学概念中的不同部分。1 t检验的历史阿瑟·健力士公司（Arthur Guinness Son & Co.）是一家由阿瑟·健力士（Arthur Guinness）于1759年在爱尔兰都柏林建立的一家酿酒公司：不过它最出名的却不是啤酒，而是《吉尼斯世界纪录大全》：1951年11月10日，健力士酒厂的董事休·比佛爵士（Sir Hugh Beaver）在爱尔兰韦

马同学图解数学 泰勒公式系列之完整公式推导

先说结论，特征函数是随机变量的分布的不同表示形式。一般而言，对于随机变量的分布，大家习惯用概率密度函数来描述。比如说：意思就是服从正态分布，对应的概率密度函数如下：虽然概率密度函数理解起来很直观，但是确实随机变量的分布还有另外的描述方式，比如特征函数。1 关于特征1.1 剪影下面是两个剪影：是同一个人吗？不知道，看不清楚，不过如果知道这两个剪影的特征，比如：名字血型身高声音...以上特征如果都一样