A matrix approach to standardizing your data

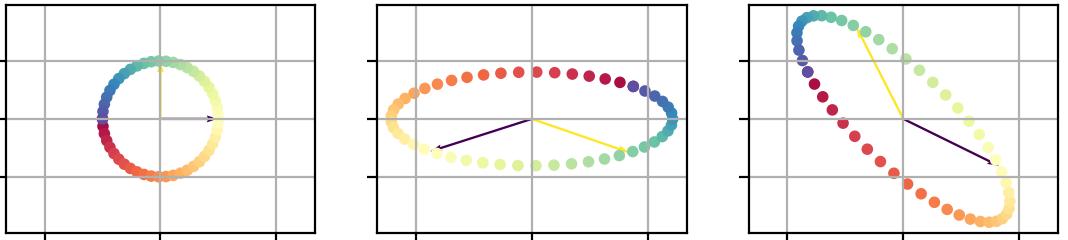
Image by author

One of the first step when dealing with new data in data-science and machine learning is often to standardize — or “scale”- your data. The most common procedure — often called Z-score Normalization — is simply to remove the mean from each column-feature, and divide it by its standard-deviation. You’re left with features that have 0-mean and 1-variance. This make every feature “comparable” in scale. The next step is then to introspect your data to find potentiel colinearity, aka correlation. If your data are not correlated at all, the resulting covariance matrix will be the identity matrix, that is each column has 1-variance, and is perfectly decorrelated from every other columns. But that never happens in the real world.

The process of whitening data consists in a transformation such that the transformed data has identity matrix as covariance matrix. This process is also called “sphering” the data. It has many application, the most known being dimensionnality reduction as done in Principal Component Analysis. Sphering your data makes your data “topologicaly” simpler, which in turns improves stability and convergence speed of numerical resolutions.

There are many ways you can “whiten” your data, and most commons ways are called PCA-whitening and ZCA-whitening.

Remember : whitening your data not only “standardize”, it also decorrelates each features.

Data matrix and covariance matrix

Let X be your data matrix with m samples as rows and n features as columns. Let’s first center the data along the columns such that each feature-columns has a mean of 0. Since the data matrix has 0-mean along columns, we can simply write the sample covariance matrix as :

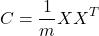
Covariance matrix

PCA-whitening

The covariance matrix C is real and symmetric, and so can be diagonalized using eigen decomposition: this means we can rewrite the covariance matrix as :

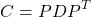
Eigen decomposition of covariance matrix

with D being a diagonal matrix with eigen values in the diagonal, and P an orthononormal matrix — also called “rotation” matrix.
We can then use D and P to whiten our data matrix X, using the linear transformation :

PCA-Whitening transformation matrix

This transformation indeed decorrelates the data with a rotation P^T, then scales the new features using D^{-1/2} so that they have unit-variance.

Here is a proof that the covariance matrix of the transformed data is the identity matrix :

Proof that W_PCA whiten data matrix X

ZCA-whitening

ZCA-whitening is really close to PCA-whitening : the difference hold in an additional rotation — or orthonormal transformation.

While PCA-whitening is done applying,

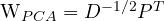
ZCA-whitening is done by applying :

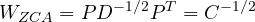
ZCA-Whitening transformation matrix

Mathematically, it can be shown that W_{ZCA} is the matrix A such that X’=XA^T has identity matrix as covariance (as expected since we are whitening our data), AND minimises

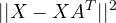
ie the whitened data is as close as possible from the original data.

Relation between PCA-whitening and ZCA-whitening

Let’s recap what we did : first decompose the centered-data covariance matrix of the input data matrix X using eigen-decomposition:

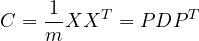
Then, PCA-whitening is done by the transformation :

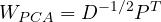
And ZCA-whitening is done by applying the transformation :

It is then easy to relate both tranformations :

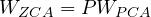
This last equation show that ZCA-whitened data is just the PCA-whitened data with an additional rotation (since P in the eigen decompostion is a rotation matrix).

Which one should I use

As you can see, PCA-whitening and ZCA-whitning are equal up to the rotation P, but we could have used any other rotation : in fact, there are an infinite number of transformations that can whiten our data.

For example, in addition to PCA-whitening and ZCA-whitening, wikipedia also mentions Cholesky whitening.

The method you should use, as always, depends on what you want :
— ZCA-whitening is the unique procedure that maximizes the average cross-covariance between each component of the whitened and original vectors
— PCA-whitening is the unique sphering procedure that maximizes the integration, or compression, of all components of the original vector X in each component of the sphered vector X’ based on the cross-covariance as underlying measure.

That is : if you plan on reducing the dimension of your data, use PCA-whitening. If you want your whitened data to be close to your original data, use ZCA whitening.

Whitening with numpy

Now that we have set the theory, let’s pratice !

We create an arbitraty data matrix X to play with, and compute its covariance matrix :

Then we decompose the covariance matrix using eigen-decomposition :

We can check that the covariance matrix is indeed C = PDP^T:

Now we compute the square-root of the inverse of D : since D is a diagonal matrix, its inverse is very simple :

Again, check that our computation is valid :

We can now compute our transformation matrices, one for PCA-whitening and one for ZCA-whitening, using the formulas from above :

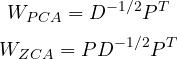
Plotting

Now that we have all the matrices we need, it’s time to do some plotting:

You should get a figure like this one :

Image by author

We can notice several things :
— to plot the original data, we passes the identity matrix as transformation matrix, since X = I X
— the covariance matrix for PCA-whitened data and ZCA-whitened data is indeed the identity matrix, so our whitening works in both cases
—you can convince yourself that the PCA-whitened data and ZCA-whitened data are equal up to a rotation
— you can see that the ZCA-whitened data colors orientation is sensibly the same as the original data, while PCA-whitened data could have had any orientation and differs a lot from original data.

Feel the transformation

Lets improve our visualisation by adding a couple of vectors to represent the initial x-axis and y-axis, as well as a colored circle.

You can picture these points as new data in the original dataset : just like our data matrix X, they have a x and y values, so they also lie in the same initial space as the original data.

Since whitening our data was done applying a linear transformation, we can apply the same transformation to those points (both arrows and the circle), and visualize how they get transformed:

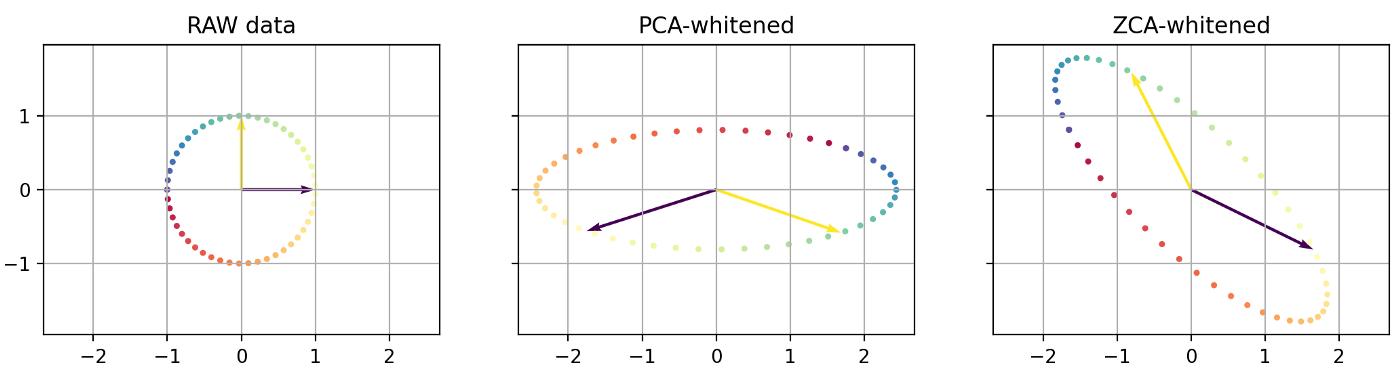
Image by author

Once again, you can see how PCA and ZCA are just a rotation appart. Also notice the general direction of the colors on the circle.

For completness, let’s superpose everything :

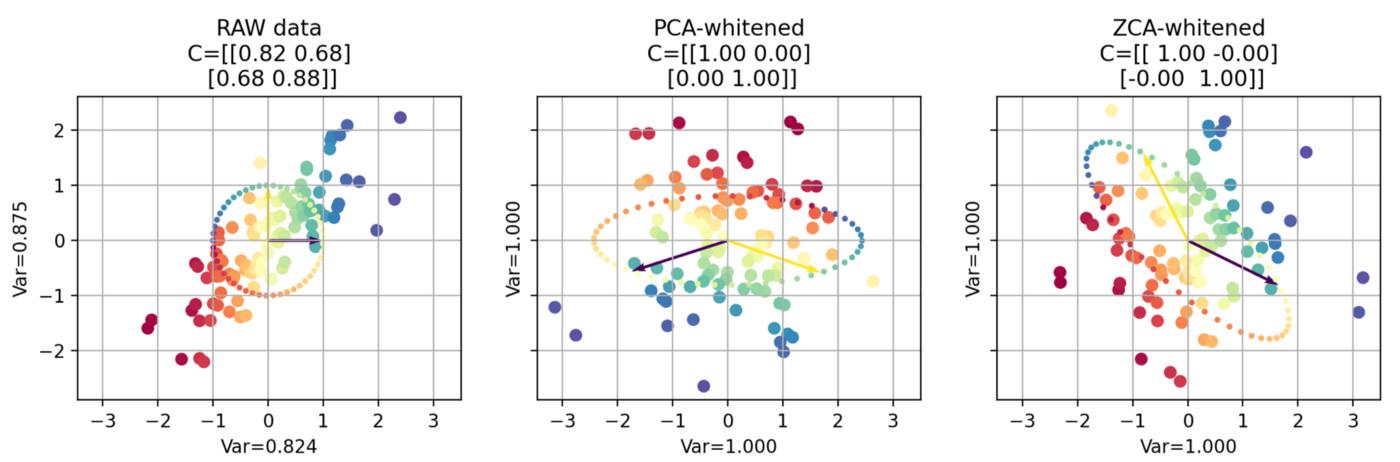
Image by author

Takeaways

Here is what you should remember from this post ;
- whitening, also called sphering, consists in transforming your data so that it has the identity matrix as its covariance matrix, that is uncorrellated data with unit variance
- there are infinite ways to whiten your data, and 2 most common methods are called PCA-whitening and ZCA-whitening
- PCA-whitening and ZCA-whitening are equivalent up to a rotation
- if you plan on reducing the dimension of your data, use PCA-whitening. If you want your whitened data to be close to your original data, use ZCA-whitening.

If you liked this post and found it informative, please subscribe, and check my other posts, they might convince you to subscribe :)

[

300-times faster resolution of Finite-Difference Method using numpy

Finite-difference method is a powerfull technique to solve complex problems, and numpy makes it fast !

towardsdatascience.com

](/300-times-faster-resolution-of-finite-difference-method-using-numpy-de28cdade4e1)

[

Deep dive into seaborn : meet the datasets

Python plotting : All you should know about handling seaborn datasets

medium.com

](https://medium.com/analytics-vidhya/deep-dive-into-seaborn-meet-the-datasets-8d08755a320b)

[

Wrapping numpy’s arrays

The container approach.

towardsdatascience.com

](/wrapping-numpys-arrays-971e015e14bb)

[

Interactive plotting the well-know RC-circuit in Jupyter

Another step into ipywidgets and matplotlib

towardsdatascience.com

](/interactive-plotting-the-well-know-rc-circuit-in-jupyter-d153c0e9d3a)

And since you read all the way down, here is a function to whiten your data that wraps it all: