简介

整流线性单位函数 ReLU 是深度学习中最常用的三种激活函数之一,包括_sigmoid (sig)_ 和_hyperbolic tangent (tan)_ 函数。它是一种_ramp_函数,有点类似于电气工程中的半波整流原理。

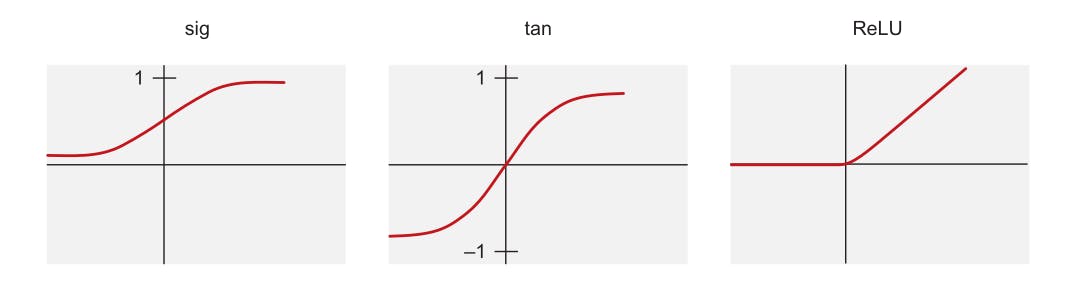图 1. 激活函数 [1]

ReLU函数

从 1960 年代后期开始,ReLU 函数开始出现在分层神经网络中视觉特征提取的背景下。后来出现了关于它具有强烈的生物学动机和数学依据的争论。它被其他激活函数接受的原因之一是它可以更好地训练更深的网络。目前,ReLU 函数可以说是深度学习中最常用的激活函数。

众所周知,ReLU 激活单元不太可能产生梯度消失问题,因为对于参数的正值,它的导数始终为 1。 -pg 44,神经网络和深度学习 2018

传统上,sigmoid 和 tanh 激活是隐藏层中最流行的选择,但 ReLU 激活近年来变得越来越流行,因为它具有更好地避免梯度消失和爆炸问题的理想特性,-pg 62 ,神经网络和深度学习 2018

优势

ReLU 激活函数极大地受益于 sparsity(一个超出本文范围的主题),它用于允许网络轻松获得稀疏表示。例如,在一个随机初始化的网络中,大约 50% 的隐藏单元被激活(具有非零输出)。这导致对神经元子集的线性计算,以及神经元活动部分的梯度流动性更强(因此消除了由于 sigmoid 或 tanh 单元的激活非线性导致的梯度消失效应)。因此,数学研究更容易,计算更便宜[2]。

有关更多信息,请查看有关深度稀疏整流器神经网络的论文

让我们介绍一些有趣的数学

在上一节中,我们将 ReLU 函数定义为某种 ramp 函数。在数学中,这种类型的函数被广泛称为正部分,由以下等式给出:

$$ \begin{方程} f^+(x) u003d \max(f(x),0) u003d \begin{cases} f(x) & \text{if}\ f(x) \gt 0 \\ 0, & \text{否则} \end{cases} \tag{1} \end{equation} $$

我们可以推广方程 \(1\) 来定义斜坡函数:

$$ \mathbf R :u003d \max(x, 0) \tag{2} $$

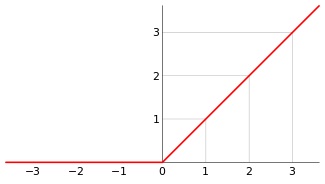图 2. 斜坡函数的图形表示 [3]

备注:直观上,我们将 \(f^+\) 取 \(f\) 的图,去掉 x 轴下的部分,让 \(f^+ \) 在那里取零值。

对于 ReLU 激活函数,它在数学上定义为其参数的正部分,由下式给出:

$$ f(x) u003d x^+ u003d \max(0,x) \tag{3} $$ 其中 \(x\) 是神经元的输入。

从方程 \(2\ \text{and}\ 3\) 我们可以看到 ramp 函数和 ReLU 函数之间的相似之处,这就是为什么 ReLU 函数的图形表示假设与 ramp 函数的形状相同。

编写 ReLU 函数

最后,我们来到了有趣的部分! 😎 ReLU 函数的数学定义使得它在代码方面很容易实现,我们可以通过编写一个简单的条件语句来计算它,或者使用 python 中的 \(max()\) 函数。本节展示了这两种方法,所以让我们开始吧!

使用条件

>>> def ReLU(x): 
        if x > 0 or x == 0:
            return x
        else:
            return 0

>>> ReLU(100)
# Returns
>>> 100
>>> ReLU(-100)
# Returns 
>>> 0

在 Python 中使用 \(max()\) 函数

>>> def ReLU(x):
        return max(0, x)

>>> ReLU(100)
# Returns 
>>> 100
>>> ReLU(-100)
# Returns
>>> 0

在实践中,您几乎不需要为任何给定任务硬编码激活函数,因为有提供此类功能的可用库,上面提供的硬编码函数都不会泛化为数组的输入,所以它是最好使用 Pytorch 和 Tensorflow 等库。我们展示了如何使用下面的这些库中的任何一个来计算 ReLU 激活函数。

使用 TensorFlow/Keras

>>> import tensorflow as tf

>>> arr = tf.constant([-10, -5, 0.0, 5, 10], dtype = tf.float32)
>>> tf.keras.activations.relu(arr).numpy()

# Returns
>>> array([ 0.,  0.,  0.,  5., 10.], dtype=float32)

**使用 Pytorch **

>>> import torch
>>> import numpy as np

>>> m = torch.nn.ReLU()
>>> arr = np.array([-10, -5, 0.0, 5, 10])
>>> t_arr = torch.tensor(arr) # convert numpy array to tensor
>>> relu = m(t_arr)
>>> print(relu)

# Returns 
>>> tensor([ 0.,  0.,  0.,  5., 10.], dtype=torch.float64)

备注:在所有方法中,请注意 ReLU 函数如何处理小于或等于零的值......它将它们返回为零!

当我们绘制 Tensorflow 或 Pytorch 方法的任一输出时,我们会得到一个类似于图 2 中给出的图形。

>>> import matplolib.pyplot as plt
>>> plt.style.use("seaborn")

# Using the output from our Pytorch implementation 
>>> plt.plot(relu)
>>> plt.show()

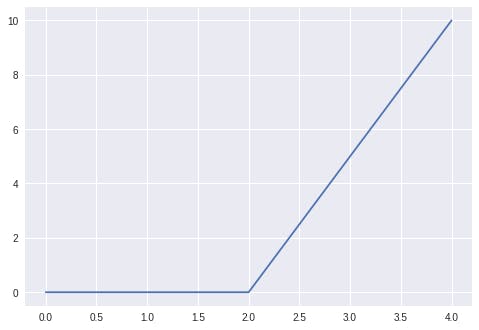图 3. ReLU 函数的 Pytorch 输出图。

结论

在本文中,我们介绍了 ReLU 激活函数并定义了一些有趣的概念,验证了它本质上是一个斜坡函数,并展示了如何使用 python 实现该函数......希望您喜欢阅读,就像我喜欢写作一样它。下次见!

参考文献

[1] 使用 Tensorflow 进行机器学习第 2 版

[2] 深度稀疏整流神经网络

[3] 斜坡函数