python中的# 中断时间序列(ITS)
统计断言干预有效性的黄金标准是随机对照实验及其简化的在线变体:A/B 测试。 📝 在 A/B 测试期间,有两个几乎相同的产品版本同时运行,它们的不同之处仅在于您要测试的假设(即红色号召性用语按钮可以转换多于蓝色按钮吗?)。用户被随机选择在实验活动期间体验两个版本中的一个(且仅一个)。 它们易于理解,易于设置(易于使用的免费工具),并且如果设计正确,它们可以排除组之间的任何协变量差异。 但是,有
统计断言干预有效性的黄金标准是随机对照实验及其简化的在线变体:A/B 测试。
📝 在 A/B 测试期间,有两个几乎相同的产品版本同时运行,它们的不同之处仅在于您要测试的假设(即红色号召性用语按钮可以转换多于蓝色按钮吗?)。用户被随机选择在实验活动期间体验两个版本中的一个(且仅一个)。
它们易于理解,易于设置(易于使用的免费工具),并且如果设计正确,它们可以排除组之间的任何协变量差异。
但是,有时无法设置 A/B 测试:
-
技术难点。有时,更改是如此广泛和复杂,以至于在技术上不可能同时运行两个不同的版本。
-
经营战略。新功能的推出将首先在某些国家/地区推出,然后在其他国家/地区推出。
-
道德问题。让一部分客户可以访问某个功能或错误修复,从而使他们比其他没有的客户具有竞争优势。
-
法律或法规要求。法规的更改成为强制性的(即 GPDR 合规性),并且应同时适用于给定国家/地区的所有客户。
-
暂时不可行。您想分析已经发生的事件(即上次Google 的搜索算法更新如何影响您的销售漏斗?)。
准实验

如果你不能做 A/B 测试,那么第二个最好的选择是准实验 [1]。
在准实验中,您的治疗组和对照组不是按完全随机过程划分的,而是按自然过程(即时间、位置等)划分的,因此由于偏度和异质差异而导致失衡的可能性要大得多。准实验的结果不会像 A/B 那样精确,但如果仔细进行,可以认为足够接近来计算估计值。
在某些情况下,就像在上一节中描述的那样,将一个控制组与一个测试组并行是不可能的,这就是中断时间序列非常方便的时候。
中断时间序列(ITS)
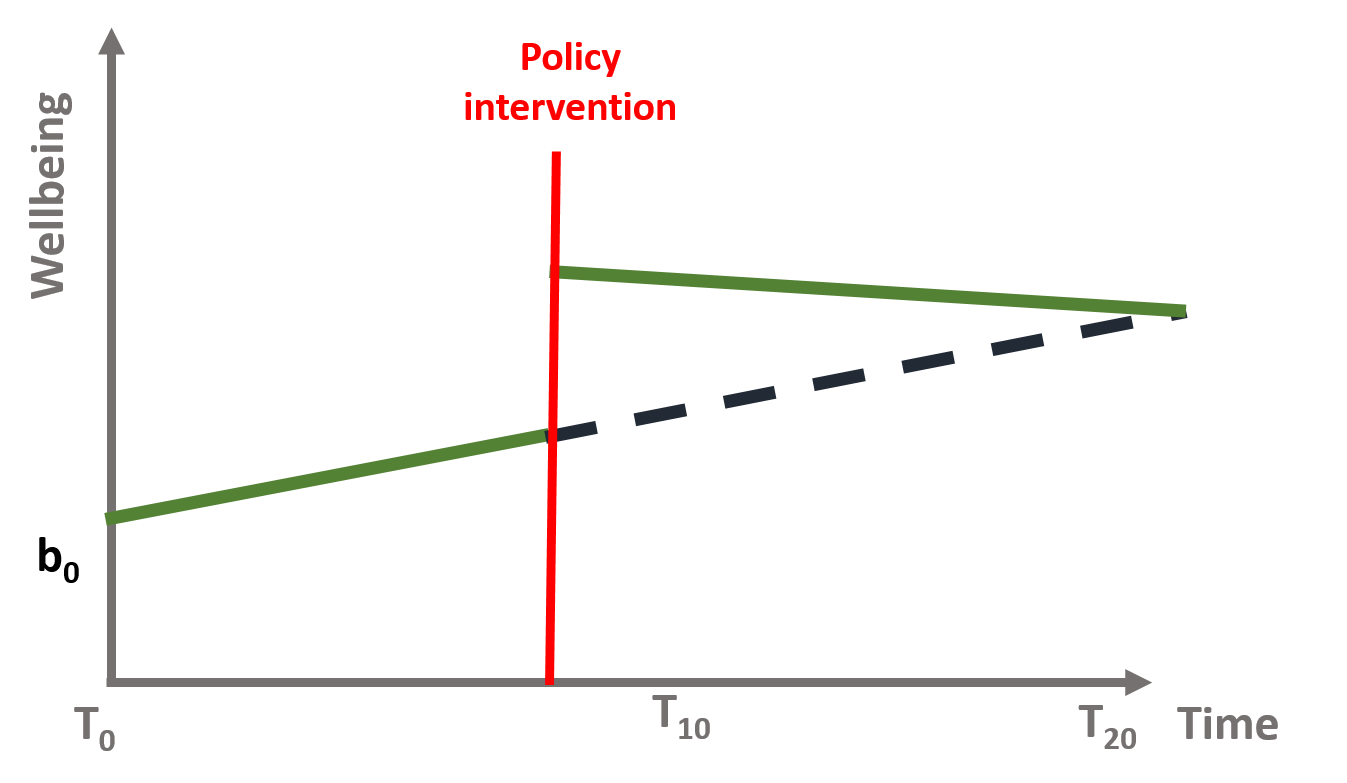
中断时间序列 (ITS) 是一种统计分析方法,涉及在已知时间点跟踪干预前后的一段时间,以评估干预的效果_在单个组/人群中_。时间序列是指一段时间内的数据,而中断是干预,是受控的外部影响或一组影响。通过时间序列的水平和斜率的变化以及干预参数的统计显着性来评估干预的效果[2]。您在干预前后的观察越多,您的模型(通常)就越稳健。由于评估是基于随着时间的推移观察单个人群,因此 ITS 设计不会因组间差异而出现问题,但容易受到随时间变化的混杂因素的影响,例如在干预期间发生的其他干预措施也可能影响结果[3]。
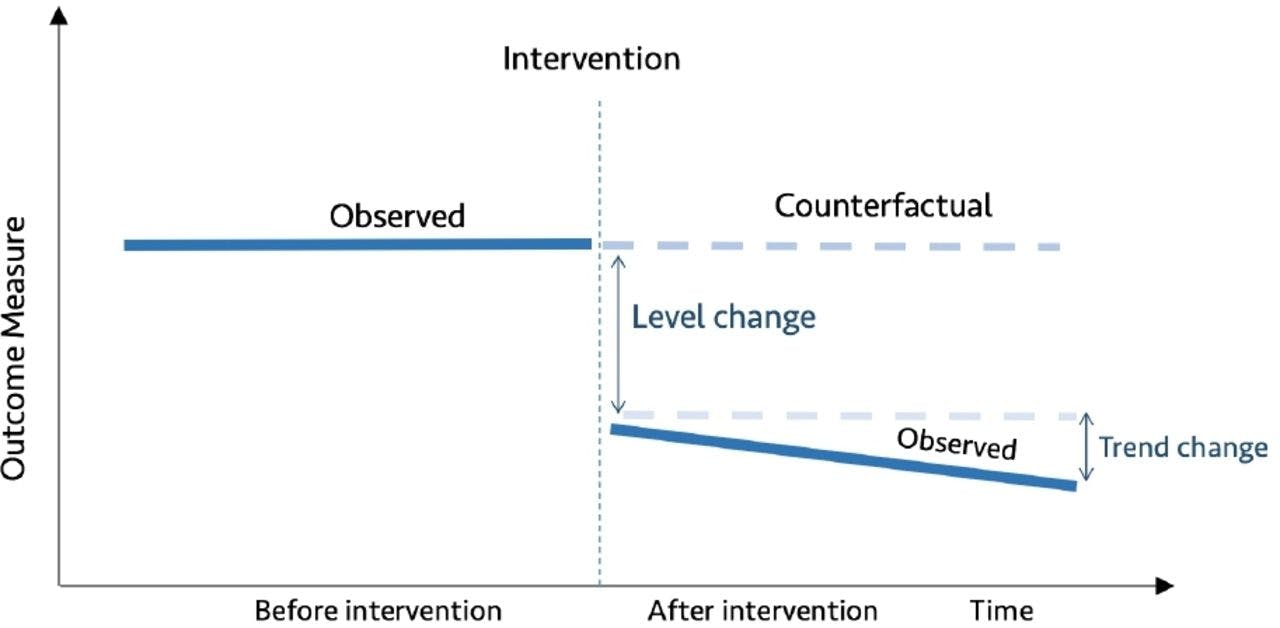
👍 中断时间序列的优势包括控制数据中的长期趋势的能力(不像 \(t\) 测试前后的 2 个时期),使用人口水平数据评估结果的能力,清晰结果的图形表示,易于进行分层分析,以及评估干预措施的预期和非预期后果的能力。
👎 中断时间序列的局限性包括:干预前后至少需要 8 个时间段来统计评估变化,难以分析在时间上紧靠在一起实施的项目的各个组成部分的独立影响,以及存在合适的对照人群。
用数学术语来说,这意味着时间序列方程(1)包括四个关键系数:
\begin{方程} Y u003d b_0 + b_1T + b_2D + b_3P + \epsilon \end{方程}
在哪里:
\(Y\) 是结果变量;
\(T\) 是一个连续变量,表示从观察期开始经过的时间;
\(D\) 是一个虚拟变量,表示在干预之前 (\(Du003d0\)) 或之后 (\(Du003d1\)) 收集的观察结果;
\(P\) 是一个连续变量,表示自干预发生以来经过的时间(干预发生之前 \(P\) 等于 \(0\));
使用 \(\epsilon\) 表示以零为中心的高斯随机误差。
反事实

如果尼奥选择了蓝色药丸会发生什么?
在 ITS 中,了解反事实很重要。反事实是指如果没有发生政策干预,Y 会发生什么。
📝反事实只是比较给定变化会发生的事情,与最初没有发生变化时应该发生的事情的简单方法。
在随机试验或 A/B 测试中,我们知道反事实的平均结果,因为实验拒绝了对照组的干预(通过随机化与干预组有些相同)。 ITS 中的一个关键假设是,在没有干预的情况下,利息趋势的结果将保持不变。
一个实际例子
Bob 经营着一个关于个人理财的大型且成功的博客。在一次网络研讨会期间,他了解到加快 Web 内容加载速度可以降低其跳出率,因此决定注册CDN服务。他在博客中添加 CDN 已经 6 个月了,他想知道他所做的投资是否降低了跳出率。
数据集
Bob 为我们提供了🗒️ 24 周的数据在添加 CDN 之前和之后的 24 周(干预)。因此,干预前的第 1 至 24 周和干预后的第 25 至 48 周有反弹率。
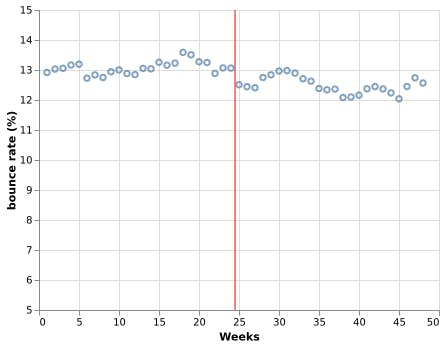
从视觉上看,开启 CDN 后跳出率似乎下降了,但下降了多少,有统计意义吗?要使用中断的时间序列分析来回答这个问题,我们首先需要准备我们的数据。
数据集准备
使用等式 (1) 表示法,我们🗒️ 丰富此数据列的值 \(D\)(0 u003d 干预前,1 后)和 \(P\)(干预开始后的周数) :
跳出率
(Y)
星期
(T)
干涉
(四)
干预周
(P)
12.92
1
0
0
13.03
2
0
0
13.06
3
0
0
13.17
4
0
0
...
...
...
...
12.04
45
1
21
12.45
46
1
22
12.74
47
1
23
12.57
48
1
24
幼稚解决方案
让我们使用statsmodels实现一个普通最小二乘 (OLS) 回归来衡量我们干预的影响:
import pandas as pd
import statsmodels.api as sm
import statsmodels.formula.api as smf
df = pd.read_csv("enriched_data.csv")
model = smf.ols(formula='Y ~ T + D + P', data=df)
res = model.fit()
print(res.summary())
带输出:
OLS 回归结果
u003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003d u003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003d
部门变量:Y R 平方:0.666
型号:OLS 调整。 R平方:0.643
方法:最小二乘 F 统计量:29.18
日期:2021 年 12 月 28 日,星期二概率(F 统计):1.52e-10
时间:14:33:50 对数似然:4.8860
观察次数:48 AIC:-1.772
Df 残差:44 BIC:5.713
Df 型号:3
协方差类型:非稳健
u003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003d u003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003d
coef 标准错误 t P>|t| [0.025 0.975]
截取 12.9100 0.096 134.225 0.000 12.716 13.104
0.0129 0.007 1.920 0.061 -0.001 0.026
D -0.5202 0.132 -3.942 0.000 -0.786 -0.254
P -0.0297 0.010 -3.115 0.003 -0.049 -0.010
u003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003d u003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003d
综合:3.137 德宾-沃森:0.665
概率(全部):0.208 雅克-贝拉(JB):1.995
偏斜:0.279 概率(JB):0.369
峰度:2.172 康德。 125 号。
u003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003d u003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003du003d
该模型估计跳出率下降了 🔻 0.52%,这种影响具有统计学意义(\(P>|t|\) 几乎为零)。
还值得注意的是,该模型估计干预后每周跳出率下降的趋势很小(平均🔻 0.0297%)但具有统计显着性趋势,这是出乎意料的,因为 CDN 在激活后仅几个小时就为整个网站提供服务。
下图描述了模型在干预前后的拟合情况以及它如何预测反事实:
start = 24
end = 48
beta = res.params
# Get model predictions and 95% confidence interval
predictions = res.get_prediction(df)
summary = predictions.summary_frame(alpha=0.05)
# mean predictions
y_pred = predictions.predicted_mean
# countefactual assumes no interventions
cf_df = df.copy()
cf_df["D"] = 0.0
cf_df["P"] = 0.0
# counter-factual predictions
cf = res.get_prediction(cf_df).summary_frame(alpha=0.05)
# Plotting
plt.style.use('seaborn-whitegrid')
fig, ax = plt.subplots(figsize=(16,10))
# Plot bounce rate data
ax.scatter(df["T"], df["Y"], facecolors='none', edgecolors='steelblue', label="bounce rate data", linewidths=2)
# Plot model mean bounce rate prediction
ax.plot(df["T"][:start], y_pred[:start], 'b-', label="model prediction")
ax.plot(df["T"][start:], y_pred[start:], 'b-')
# Plot counterfactual mean bounce rate with 95% confidence interval
ax.plot(df["T"][start:], cf['mean'][start:], 'k.', label="counterfactual")
ax.fill_between(df["T"][start:], cf['mean_ci_lower'][start:], cf['mean_ci_upper'][start:], color='k', alpha=0.1, label="counterfactual 95% CI");
# Plot line marking intervention moment
ax.axvline(x = 24.5, color = 'r', label = 'intervention')
ax.legend(loc='best')
plt.ylim([10, 15])
plt.xlabel("Weeks")
plt.ylabel("Bounce rate (%)");
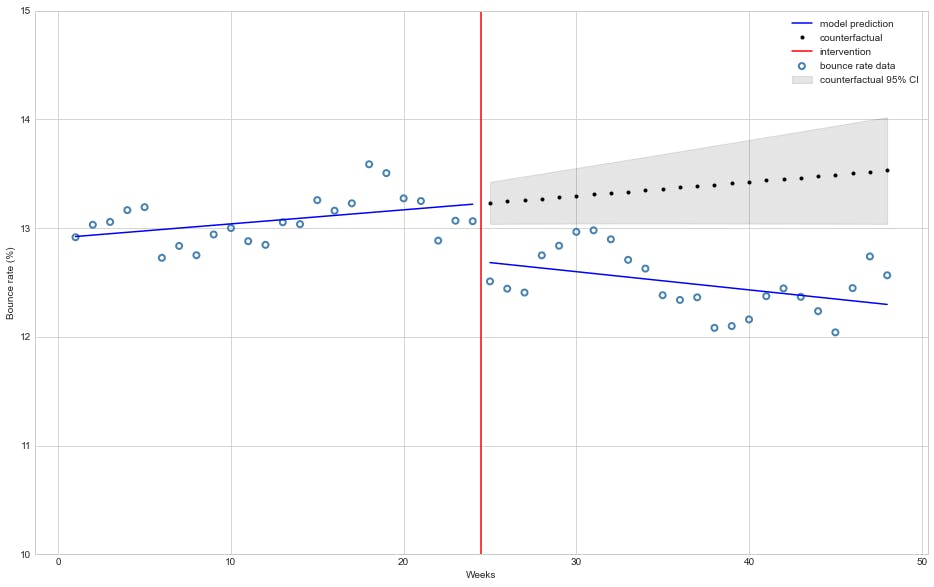
幼稚方法的问题

OLS(普通最小二乘)回归有七个主要假设但在本文中为了简洁起见,我们将只关注两个:
-
个体观察是_独立的_。
-
残差服从正态分布。
我们首先检查残差的正态性:
我们可以对残差应用Jarque-Bera 检验来检查它们的偏度和峰度是否符合正态分布(\(H_0\):残差分布服从正态分布)。我们的statsmodelsOLS汇总输出显示了Prob(JB): 0.369,对于 0.05 的标准 \(\alpha\) 级别,我们不允许丢弃零假设 (\(H\_0\))。
让我们绘制残差分布:
res.resid.plot(kind="kde")
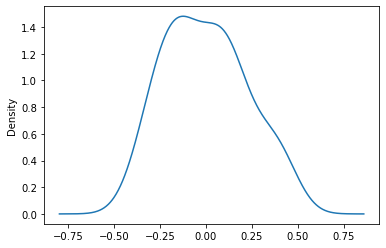
对于小型数据集(少于 50 个点),这看起来足够高斯。
总体而言,不能令人信服地驳斥残差正态性的假设。 ✅
检查观察的独立性:
Durbin-Watson 统计量检验残差是否与其直接前任相关,也就是说,它们是否在滞后 1 或 \(AR(1)\) 处具有自相关。它的值范围从 0 到 4,小于 1.5 的值表示正自相关,而大于 2.5 的值表示负自相关。
如果我们再次查看我们的 OLS汇总输出,我们将观察到 Durbin-Watson 统计量的值为 0.665,这表明强烈的正数 \(AR(1)\)。
让我们绘制残差,看看我们是否可以观察到这种自相关:
import altair as alt
rules = alt.Chart(pd.DataFrame({
'residuals': [0.0],
'color': ['black']
})).mark_rule().encode(
y='residuals',
color=alt.Color('color:N', scale=None)
)
residual_plot = alt.Chart(res_df).mark_point().encode(
x=alt.X('Weeks'),
y=alt.Y('residuals')
)
rules + residual_plot
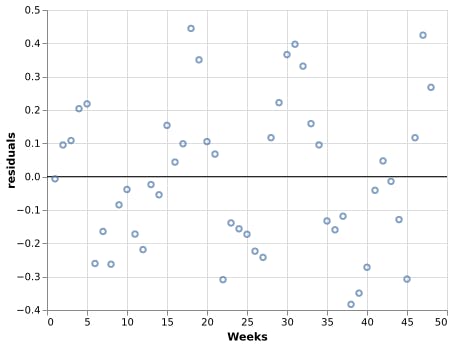
请注意高于/低于零的残差如何使大多数点暂时接近它也高于/低于零,这与 OLS ❌ 的观察假设的独立性背道而驰。
📝在分析时间序列数据的实践中,自相关的存在是规则而不是例外,因为通常有助于给定观察的因素往往会持续一段时间。
自回归模型解决方案
自回归模型指定每个观测值线性依赖于先前的观测值。
因此,阶 \(p\) (\(AR(p)\)) 的自回归模型可以写为
\begin{方程} y_t u003d c + \phi_1 y_{t-1}+ \dots + \phi_p y_{t-p} + \epsilon_t \end{方程}
在哪里:
\(y_t\):在时间 \(t\) 的观察,
\(y_{t-i}\): 观察时间 \(t - i\),
\(\phi_i\):有多少观察系数 \(y_{t - i}\) 与 \(y_t\) 相关,
\(\epsilon_t\):在时间 \(t\) 处的白噪声(\(\mathcal{N}(0, \sigma2)\))。
自相关
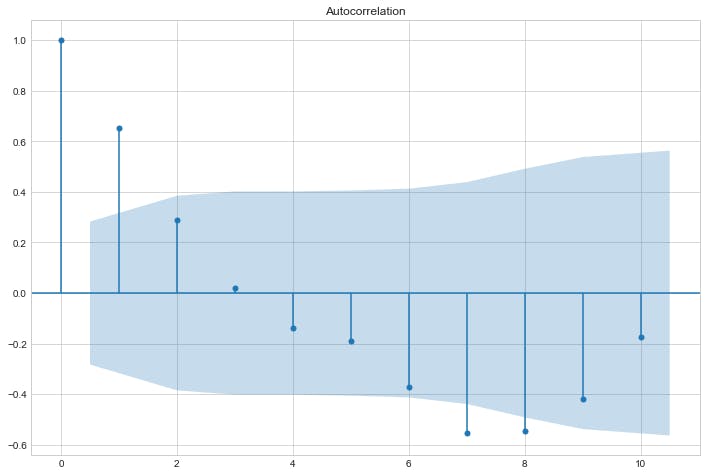
为了评估观察与过去观察的相关程度,绘制自相关图很有用,如下所示:
sm.graphics.tsa.plot_acf(res.resid, lags=10)
plt.show()
偏自相关
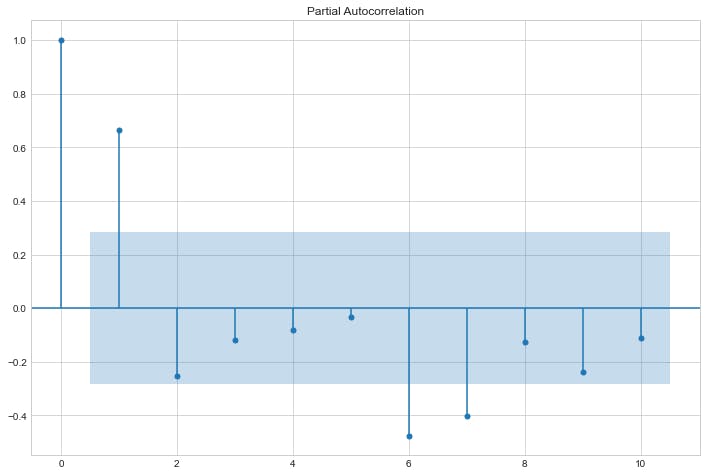
滞后 \(p\) 处的偏自相关是在消除由于较短滞后项引起的任何相关性的影响后产生的相关性。
sm.graphics.tsa.plot_pacf(res.resid, lags=10)
plt.show()
型号选择
该理论指出,在自回归模型中,其自相关图应描绘指数衰减,滞后数 \(p\) 应使用其 \(p\) 最相关滞后从偏自相关图中获取。将理论应用于我们上面的图,我们得出结论,我们的模型是滞后 1 的自回归,也称为 AR(1)。
有马
在统计中ARIMA代表自回归综合移动平均模型,并且可以通过名称推断 AR 模型是 ARIMA 的特例,因此 AR(1) 等效于 ARIMA(1,0,0)。
我们可以使用statsmodelsARIMA 将 AR(1) 过程建模到我们的数据集,如下所示:
from statsmodels.tsa.arima.model import ARIMA
arima_results = ARIMA(df["Y"], df[["T","D","P"]], order=(1,0,0)).fit()
print(arima_results.summary())
输出:
SARIMAX Results
==============================================================================
Dep. Variable: Y No. Observations: 48
Model: ARIMA(1, 0, 0) Log Likelihood 18.574
Date: Thu, 30 Dec 2021 AIC -25.148
Time: 01:51:46 BIC -13.921
Sample: 0 HQIC -20.905
- 48
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 12.9172 0.279 46.245 0.000 12.370 13.465
T 0.0121 0.016 0.767 0.443 -0.019 0.043
D -0.5510 0.273 -2.018 0.044 -1.086 -0.016
P -0.0238 0.021 -1.155 0.248 -0.064 0.017
ar.L1 0.6635 0.138 4.803 0.000 0.393 0.934
sigma2 0.0267 0.006 4.771 0.000 0.016 0.038
===================================================================================
Ljung-Box (L1) (Q): 1.00 Jarque-Bera (JB): 0.15
Prob(Q): 0.32 Prob(JB): 0.93
Heteroskedasticity (H): 1.44 Skew: -0.05
Prob(H) (two-sided): 0.47 Kurtosis: 3.25
===================================================================================
自回归模型估计跳出率平均下降了 🔻 0.55%,这种影响具有统计学意义 (\(P>|t| u003d 4.4\% \),小于我们的 \(\alpha u003d 5\ % \))。
但是,与之前的OLS模型不同,自回归模型并没有估计干预后每周跳出率下降的统计显着趋势,这符合我们的预期。
模型估计(带有反事实预测)如下图所示:
from statsmodels.tsa.arima.model import ARIMA
start = 24
end = 48
predictions = arima_results.get_prediction(0, end-1)
summary = predictions.summary_frame(alpha=0.05)
arima_cf = ARIMA(df["Y"][:start], df["T"][:start], order=(1,0,0)).fit()
# Model predictions means
y_pred = predictions.predicted_mean
# Counterfactual mean and 95% confidence interval
y_cf = arima_cf.get_forecast(24, exog=df["T"][start:]).summary_frame(alpha=0.05)
# Plot section
plt.style.use('seaborn-whitegrid')
fig, ax = plt.subplots(figsize=(16,10))
# Plot bounce rate data
ax.scatter(df["T"], df["Y"], facecolors='none', edgecolors='steelblue', label="bounce rate data", linewidths=2)
# Plot model mean bounce prediction
ax.plot(df["T"][:start], y_pred[:start], 'b-', label="model prediction")
ax.plot(df["T"][start:], y_pred[start:], 'b-')
# Plot counterfactual mean bounce rate with 95% confidence interval
ax.plot(df["T"][start:], y_cf["mean"], 'k.', label="counterfactual")
ax.fill_between(df["T"][start:], y_cf['mean_ci_lower'], y_cf['mean_ci_upper'], color='k', alpha=0.1, label="counterfactual 95% CI");
# Plot line marking intervention moment
ax.axvline(x = 24.5, color = 'r', label = 'intervention')
ax.legend(loc='best')
plt.ylim([10, 15])
plt.xlabel("Weeks")
plt.ylabel("Bounce rate (%)");
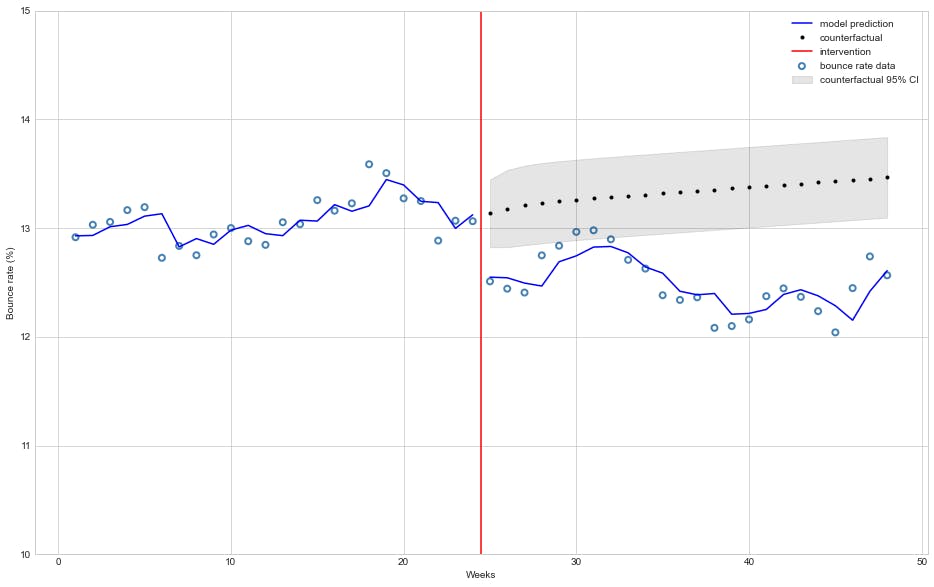
我们可以清楚地看到,ARIMA(1, 0, 0) 模型比 OLS 模型更适合我们的数据集。
ARIMA残差分析
我们的自回归模型的摘要显示了一个Prob(JB): 0.93,它与正态分布残差的零假设兼容。 ✅
Ljung-Box Q 检验验证残差是否独立分布(它们没有表现出序列自相关)为 \(H_0\)(零假设)。由于Prob(Q): 0.32远高于标准 \(\alpha u003d 0.05\),因此没有证据表明 ARIMA 残差中存在序列自相关。 ✅
现在让我们看一下残差qqplot以检查它们是否服从正态分布:
import scipy as sp
from statsmodels.graphics.gofplots import qqplot
fig, (ax1, ax2) = plt.subplots(1,2, figsize=(16,8))
sm.qqplot(res.resid, sp.stats.t, fit=True, line="45", ax=ax1);
ax1.set_title("OLS qqplot");
sm.qqplot(arima_results.resid, sp.stats.t, fit=True, line="45", ax=ax2);
ax2.set_title("ARIMA qqplot");
plt.show();
! zwz 100120 qq plot-side by side.png](https://cdn.hashnode.com/res/hashnode/image/upload/v1641160378089/BySYwsDvv.png?auto=compress,format&format=webp)
我们可以观察到 ARIMA(1,0,0) 模型残差不仅通常是正态分布的,因为它们比 OLS 模型更适合理论分位数。 ✅
总结
A/B 测试是一种最强大、最值得信赖的方法,可以在完全实施之前衡量修改/更改的影响,这就是它们如此广泛使用的原因。
但是,在某些情况下,A/B 测试是不可行的,此时准实验的知识对于获得对变化影响的统计合理测量值变得有价值。
在这篇文章中,我们展示了为什么普通最小二乘 (OLS) 线性回归不是时间序列数据的良好建模方法,因为它们通常呈现出违反 OLS 某些假设的不可忽略的自相关。
我们通过一个示例演示了如何使用 python(statsmodels、matplotlib、altair和pandas)来可视化残差并绘制自相关和偏自相关图表以找出自回归模型的滞后,然后使用statsmodels实现 ARIMA 模型以观察更准确的和精确的分析以及如何解释 OLS 和 ARIMA 的statsmodels模型输出。
我们还展示了如何在单个图表中绘制模型估计的干预前后时间段(平均值和 95% 置信区间)及其各自的反事实。
参考文献
[1] Shopify 工程:如何使用准实验和反事实来打造出色的产品。
[2] 维基百科:中断的时间序列。
[3] 坎贝尔 DT,斯坦利 JC。用于研究的实验和准实验设计。马萨诸塞州波士顿:Houghton Mifflin,1963 年。
更多推荐
 已为社区贡献126473条内容
已为社区贡献126473条内容








所有评论(0)