【大模型知识点】位置编码——绝对位置编码，相对位置编码，旋转位置编码RoPE（附代码）

本文介绍了大模型中常见的绝对位置编码和相对位置编码方法，如transformer的正余弦位置编码，可学习位置编码，RoPE和ABiLi

自信的小螺丝钉

4988人浏览 · 2025-03-09 21:43:35

自信的小螺丝钉 · 2025-03-09 21:43:35 发布

由于Transformer 中的自注意模块具有置换不变性（不关心输入序列的顺序），因此需要使用位置编码来注入位置信息以建模序列，使模型能够区分不同位置的 token，并捕捉序列的顺序关系。

在介绍一些位置编码方法前，首先说明，一个好的位置编码方法需要具备怎样的特性：

唯一性： 每个位置应该有一个唯一的编码，以确保模型能够区分序列中的不同位置。如果两个位置共享相同的编码，模型将无法区分它们，从而导致混淆
连续性： 位置编码应该是连续的，相邻位置的编码应该相似，连续性有助于模型捕捉序列中元素之间的局部依赖关系。如果位置编码在相邻位置之间突变，模型可能难以学习到平滑的序列模式
可扩展性： 位置编码应该能够处理比训练时更长的序列（即具有外推性），例如，Transformer的正弦和余弦位置编码由于其周期性，能够为更长的序列生成合理的编码
捕获相对位置信息： 位置编码应该能够捕获序列中元素之间的相对位置关系（例如，位置5和位置6的编码应该比位置5和位置10的编码更接近）
远程衰减特性： 远程衰减特性是指随着序列中元素之间相对位置的增加，位置编码的内积逐渐减小。这种特性有助于模型区分远距离和近距离的位置关系。这种特性有助于模型专注于更相关的局部信息，同时减少对远距离噪声的敏感性
高效性： 位置编码的计算和存储应该是高效的，尤其是在处理长序列时。复杂的位置编码方法可能会增加计算开销，从而影响模型的训练和推理速度

接下来介绍一些位置编码方法，主要可以分为绝对位置编码和相对位置编码。

1.绝对位置编码

绝对位置编码是为每个序列中的位置分配唯一的编码，无论它与其他位置的相对关系如何。每个位置的编码是固定的，并与具体的输入数据无关。常见方法有正弦/余弦编码和可学习编码：

1）正弦/余弦编码（Sinusoidal Encoding）：

首先补充背景知识：

正弦/余弦函数：
波长： 是指函数在一个完整周期内所覆盖的距离或时间间隔
频率： 是指函数在单位时间或单位距离内重复的次数
波长与频率：

使用正弦和余弦函数生成位置编码，公式如下：

i的范围是0~d/2-1

位置编码代码：

import torch 
import torch.nn as nn

class Sinusoidal_position_embed(nn.Module):
    def __init__(self,d_model,max_len):
        super().__init__()
        self.d_model=d_model
        self.max_len=max_len
        # pe :(max_len,d_model)
        pe = torch.zeros(max_len,d_model)
        # 左闭右开
        # position : (max_len,1)
        position = torch.arange(0,max_len).unsqueeze(1).float()
        # div_term : (d_model//2,)
        div_term = torch.exp(torch.arange(0,max_len,2).float()*(-torch.log(10000)/d_model))
        # 偶数位置: (max_len, d_model//2)
        pe[:,0::2] = torch.sin(position * div_term)
        # 奇数位置: (max_len, d_model//2)
        pe[:,1::2] = torch.cos(position * div_term)
        #  pe: (1, max_len, d_model)
        self.pe = pe.unsqueeze(0)
    		
    def forward(self,x):
        # x: (batch_size, seq_len, d_model)
        _,seq_len,_ = x.shape
        # 根据输入序列的实际长度seq_len，截取对应的位置编码并与输入特征相加，将位置信息注入到序列中
        return x + self.pe[:,:seq_len,:]

位置编码测试并可视化：

import matplotlib.pyplot as plt

# 可视化位置编码
d_model = 512
max_len = 400
pos_encoder = PositionalEncoding(d_model, max_len)
pe = pos_encoder.pe.squeeze().numpy()

plt.figure(figsize=(12, 6))
plt.imshow(pe, cmap='viridis')
plt.colorbar()
plt.title('Positional Encoding Visualization')
plt.xlabel('Embedding Dimension')
plt.ylabel('Position')
plt.show()

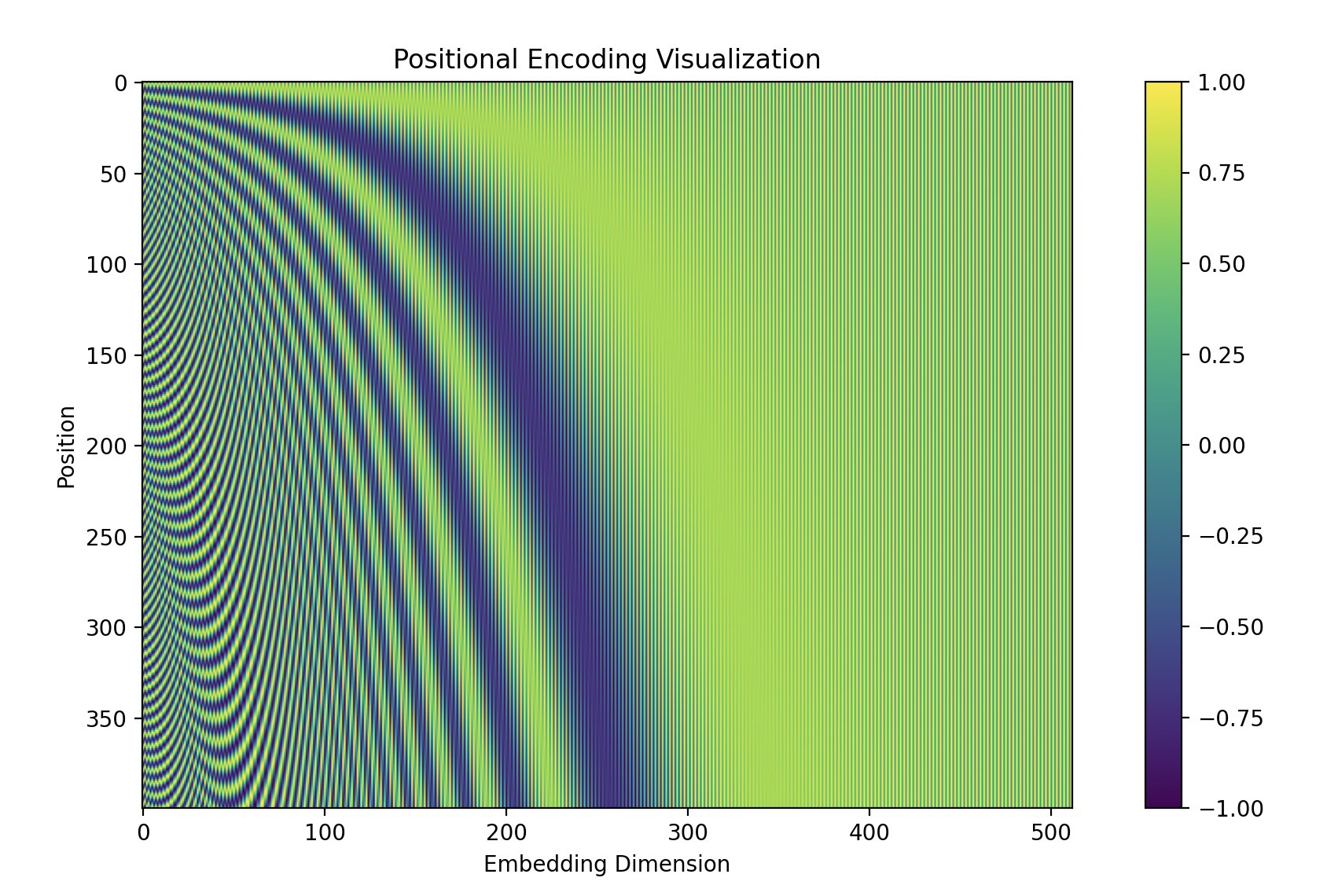
在这里插入图片描述

这样编码位置的特点（结合上图理解）：

低维度（小i）时，波长小，频率大，位置编码随位置 pos 的变化较快，对位置变化非常敏感，适用于捕捉短距离信息，即局部依赖关系
高维度（大i）：波长大，频率小，位置编码随位置 pos 的变化较慢（在高维度上，即使 pos 变化很大，因为波长大，即分母大，正弦和余弦的值仍然变化得很缓慢，也就是说两个位置很远（pos相差大）的token，在高维度的编码仍然可能相似，这种特性使得模型能够利用高维度信息来识别长距离的相似性，并捕捉远距离 token 之间的联系，对于NLP 任务中需要捕捉长距离依赖的情况（如长句子、长文档的建模）特别有帮助
不同维度（i）的编码具有不同的波长，使得 Transformer 既能关注短距离依赖，又能捕捉长距离信息，兼顾短期记忆和长期记忆
周期性与外推性： 外推性指的是模型能够处理比训练时更长的序列，正弦和余弦函数的周期性特性使得位置编码能够自然地扩展到训练时未见过的序列长度。具体来说，正弦和余弦函数的周期性意味着其值会随着输入位置的增加而重复出现，即使位置索引pos 超过了训练时的最大值，位置编码仍然能够通过函数的周期性生成有意义的值，这种重复性使得模型能够通过已学习的模式来处理更长的序列，覆盖更长的序列范围

这个编码位置中的10000起什么作用？可以换成别的数字吗？

作用： 调节位置编码的频率范围

10000决定了位置编码的频率范围。较大的值（如10000）会使频率较低，编码变化更平缓，相邻位置的编码差异较小。较小的值（如1000）会使频率较高，编码变化更剧烈，相邻位置的编码差异较大。

10000这个值决定了位置编码函数的波长较大（周期大），频率较低，使得不同位置的编码在向量空间中具有足够的区分性（如果频率较大，位置编码经常出现重复值，则每个位置的编码区分度不够大），10000这个数字的取值规律是： 小的值更适合短序列任务，但小的值在长序列任务中可能会导致位置信息的变化过于频繁和剧烈，大的值适合长序列任务。

将上述代码中的10000修改为1000，通过可视化查看位置编码的频率变化：
可以看到，相比上图，位置编码在同一位置上的变化频率更高（高维度更明显）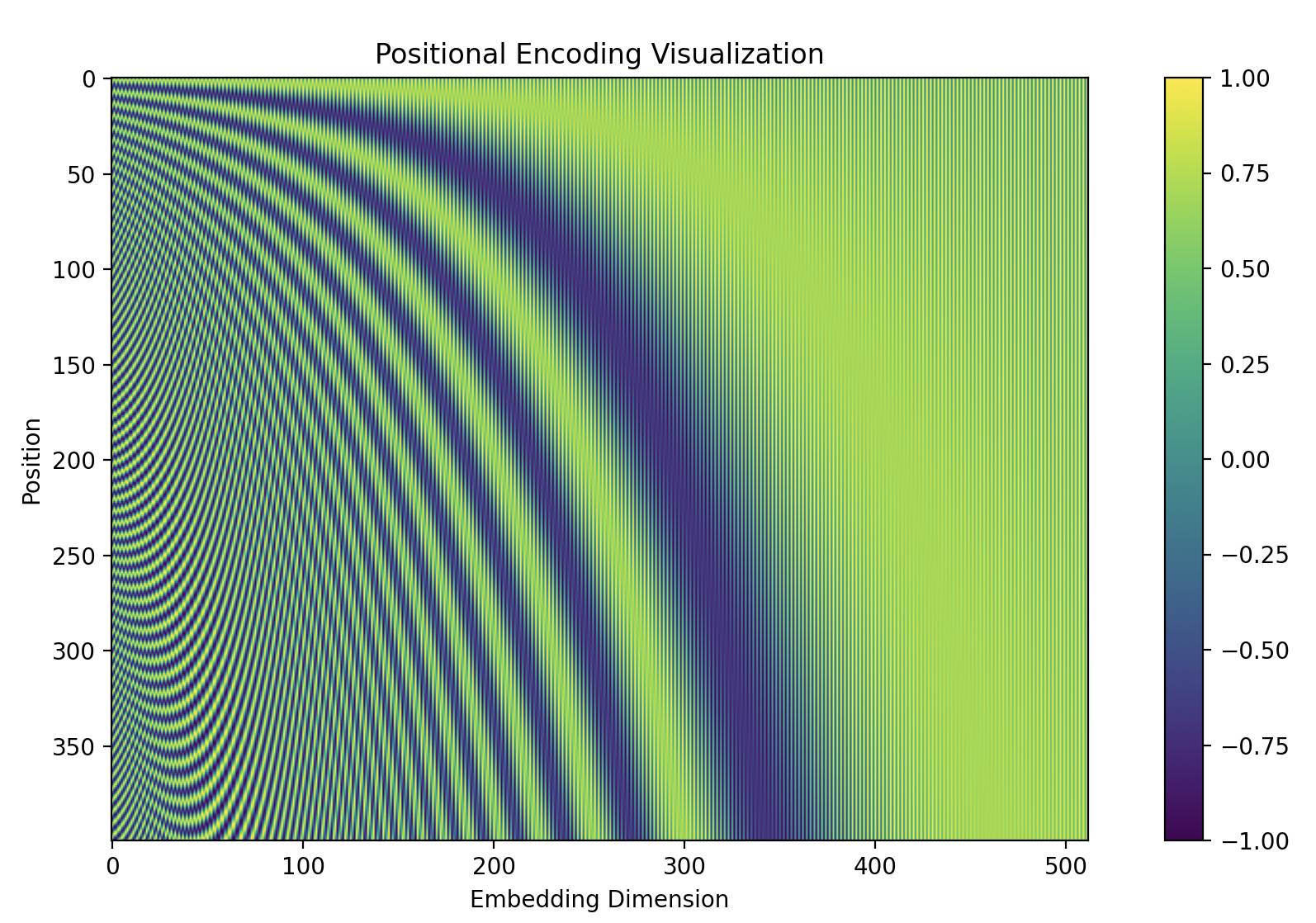
在这里插入图片描述

2）可学习编码（Learned Positional Encoding）

将位置编码向量作为可学习的参数，允许模型根据任务需求自动调整位置表示。与如正弦-余弦编码相比（通过固定的数学公式得到），可学习的位置编码更加灵活，能够根据具体任务和数据集调整位置编码，但缺点是需要学习更多的参数，并且对于不同的任务，模型可能会过拟合于某些特定的位置信息。在训练过程中，模型通过反向传播优化这些位置编码向量，使其能够更好地捕捉任务所需的位置信息。

2.相对位置编码

相对位置编码不是编码绝对位置，而是编码两个位置之间的相对关系，这种方法不必完整建模每个输入的位置信息，而是在算 Attention 的时候考虑当前位置与被 Attention 的位置的相对距离，与绝对位置编码相比，相对位置编码可以推广到比训练序列更长的序列（外推性）

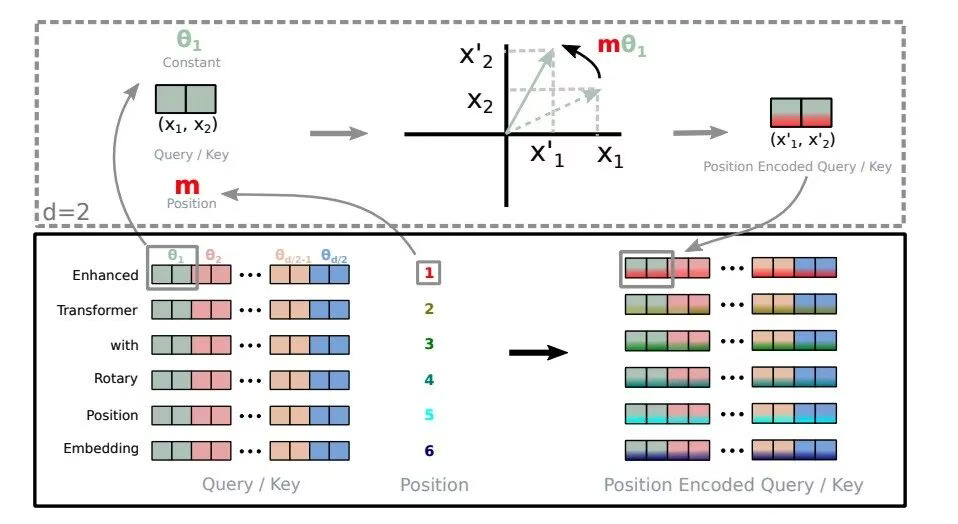
1） Rotary Position Embedding（RoPE）：

RoPE以绝对位置编码形式实现的相对位置编码，它通过将一个向量旋转某个角度，为其赋予位置信息。具体操作是对attention中的q, k进行旋转变换，使其自带相对位置信息，然后用更新的q,k向量计算attention，得到的内积就会引入相对位置信息了

RoPE已成为主流选择，代表模型有： LLaMA、PaLM

首先我们说明了RoPE是通过旋转使得向量带有位置信息的，那么我们介绍以下数学上的旋转：

此图参考自：图解RoPE旋转位置编码及其特性

根据以上的介绍，我们知道通过旋转可使得向量带有位置信息，那么RoPE怎么将这个思想带入Transformer架构中的呢？对Attention中的q（位置m）, k（位置n）进行旋转变换，使其自带位置信息，然后用更新的q,k向量通过内积计算注意力得分，得到的内积就会引入相对位置信息（两个位置的差值）了。

让 $R_m$ 表示查询向量 $q_m$ （位置m）的旋转矩阵， $R_n$ 表示键向量 $k_n$ （位置n）的旋转矩阵，那么旋转后的查询向量 $q_m' = R_mq_m$ ,旋转后的键向量 $k_n' = R_nk_n$ , 旋转后的向量引入了位置信息，计算注意力得分如下：

$Attention(q_m' ,k_n' ) = Softmax(\frac{q_m'^Tk_n'}{\sqrt{d_k}})$

小问题：

这里的注意力机制计算为什么不是 $qk^T$ ，而是 $q^Tk$ ？他们的差异在于：向量是按“列向量”还是按“行向量”来表示，下面详细需要解释一下：

一般的注意力机制计算是 $qk^T$ 表示的，这时 $q$ 和 $k$ 是行向量，维度是 $\times d$ ，那么 $qk^T$ 的维度是 $\times n$ 。而上面的RoPE的注意力计算是 $q^Tk$ ，是因为这里 $q$ 和 $k$ 是列向量，维度是 $\times n$ ，那么 $q^Tk$ 的结果维度还是 $\times n$ 。

为什么要这样呢？

我的理解：RoPE的的本质是希望有一个位置编码函数可以实现让 $q$ 和 $k$ 的内积结果包含他们的相对位置（m-n）这个信息， $q^Tk$ 比 $qk^T$ 更有助于实现。

下面介绍为什么 $q_m'^Tk_n'$ 中包含他们的相对位置（m-n）这个信息?
$q_m'^Tk_n'=(R_mq_m)^T(R_nk_n)=q_m^TR_m^TR_nk_n$

而 ${R_m}^TR_n=R_{n-m}$ ，即：
$q_m'^Tk_n'=(R_mq_m)^T(R_nk_n)=q_m^TR_{n-m}k_n$

那么 $q_m'^Tk_n'$ 中就包括了相对位置（m-n）这个信息，下面是 ${R_m}^TR_n=R_{n-m}$ 的证明：

所以 ${R_m}^TR_n=R_{n-m}$

好的，介绍到这里我们就知道了，RoPE向Q,K引入旋转矩阵 $R_m$ 和 $R_n$ ，使他们带有位置信息，而他们的内积可以用 $R_{m-n}$ 表示， $R_{m-n}$ 包含了Q,K的相对位置信息，使得模型能够更好地捕捉序列中元素之间的相对位置关系。

在最终总结之前，先重温一下二维向量的旋转：

二维向量旋转通过旋转矩阵实现角度θ的线性变换，而旋转矩阵则通过三角函数将二维向量绕原点旋转θ角度，保持向量长度不变。

在RoPE中，对于序列中第 m 个位置的向量，我们将其旋转角度 mθ。位置0：不旋转位置1：旋转 θ。位置2：旋转 2θ。位置m：旋转 mθ。其中θ是旋转角度， $θ=10000^{-2j/d}, 0<=j<d/2$ ，其中 j 是维度索引，d是向量维度，类似正余弦位置编码。

RoPE如何将二维向量的旋转扩展到多维呢？如真实的词向量通常是512维或768维，我们不能直接应用2D旋转。

解决办法：将高维向量分解成多个2D平面，将512维向量转化为256个二维平面，然后每个平面独立使用不同的旋转频率（ $θ=10000^{-2j/d}$ ）进行旋转, 如下图是一个位于m位置的 d 维向量的旋转矩阵 $R_m$ :

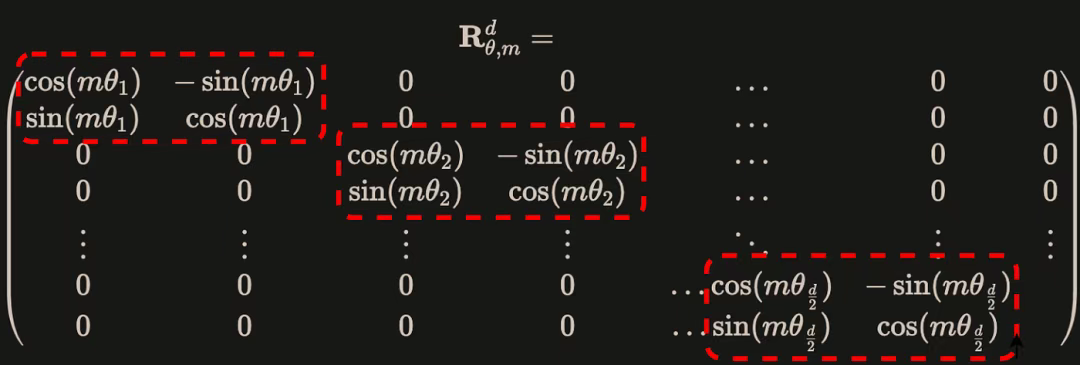
假设这个d维向量是 $q_0,q_1,···q_{d-1}$ ，那么旋转过程如下：

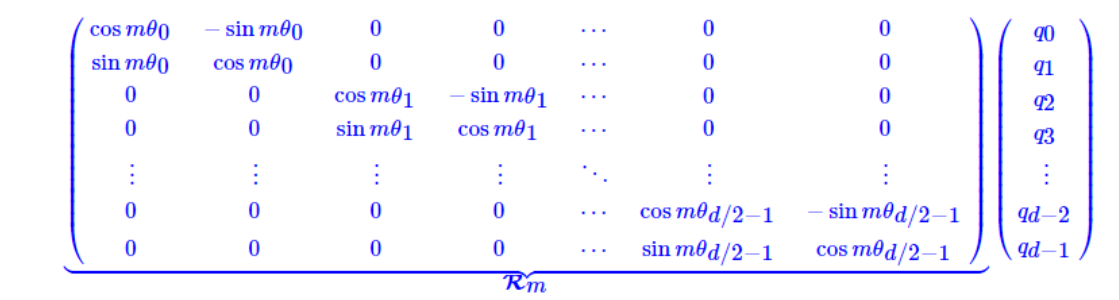
在这里插入图片描述

（这里是相邻维度一对旋转，和下面的代码实现有点不一样，注意区分）

这里是一张旋转多维向量的示意图：

最后，总结RoPE旋转位置编码的做法如下：

这里的 $\theta$ 借鉴了transformer中正余弦位置编码的思想：

低维度（小i）时，波长小，频率大，适合捕捉短距离依赖
高维度（大i）时，波长大，频率小，适合捕捉长距离依赖

现在总结RoPE的优点：

显式建模相对位置信息：通过旋转矩阵显式地建模相对位置关系
外推性：能够处理比训练时更长的序列，具有良好的外推性
多尺度位置编码：通过不同维度的旋转角度捕捉不同距离的依赖关系（ $\theta$ ）
计算高效：旋转矩阵的计算简单高效，不会引入额外的计算负担。

好了，上面介绍了RoPE的原理，但具体实现又是另一回事，下面介绍RoPE的实现： 首先说明，RoPE 通常通过复数旋转实现位置编码，为什么使用复数呢？

复数是形如： $z = a + bi$ 的数，可与平面直角坐标系（复平面） 中的点一一对应：

复平面的 x 轴 称为 “实轴”，对应复数的实部 a；
复平面的 y 轴 称为 “虚轴”，对应复数的虚部 b；
复数 $z = a + bi$ 完全等价于复平面上的点 (a, b)，也等价于从原点指向该点的向量。

复数的极坐标形式和指数形式如下：

在这里插入图片描述
复数的旋转：对于复数 z = x + yi，旋转 θ 角度后的结果为：

z' = z * (cos θ + i sin θ) = (x cos θ - y sin θ) + i(x sin θ + y cos θ)

在向量空间中，这等价于：

x' = x cos θ - y sin θ
y' = x sin θ + y cos θ

介绍完了复数旋转的数学基础，再介绍RoPE的实现：

假设位于第 $m$ 个位置的为token向量 $x$ （实际中为对应的q, k向量）的维度为 $d$ ，RoPE将其分为个 $d /2$ 二维向量对：

$x_0,x_1),(x2,x_3) ···（x_{d-2},x_{d-1}）$ ,每个二维向量对被视为一个复数，如 $x_{2i},x_{2i+1})$ 的实部是 $x_{2i}$ ，虚部 $x_{2i+1}$ ，对应的旋转角度为 $mθ_i$ , $θ_i=10000^{-2i/d}$

RoPE的代码：

import torch 
import torch.nn as nn

def precompute_rope_matrix(max_len,d_model):
    """
    生成旋转位置编码矩阵
    参数：
        max_len: 最大position embedding长度，默认为32768。
        d_model: 嵌入维度，默认为512。
    返回：
        旋转位置编码矩阵
    """
    theta = 10000.0
    # 频率,决定不同维度的旋转速度 shape: (d_model//2,)
    freqs = 1.0 / (theta ** (torch.arange(0,d_model,2).float() / d_model))
    # 位置,[0, 1, 2, ..., max_len-1]  shape: (max_len, 1)
    t = torch.arange(max_len,dtype=torch.float32)
    # 计算位置和频率的外积，得到每个位置在各维度的角度值 freqs[m,i] = t[m] * freqs[i]，表示位置 m 在维度 i的旋转角度
    # freqs[m,i] 即旋转位置编码矩阵, 表示位置和频率的乘积 [max_len, d_model//2]
    freqs = torch.outer(t,freqs).float()
    # 计算余弦和正弦值，freqs_sin 和 freqs_cos 是预计算的正弦和余弦矩阵，用于对查询（query）和键（key）向量进行旋转操作。
    # freqs_sin 和 freqs_cos 具体含义：存储每个位置在不同维度上的旋转角度的正弦和余弦值
    # freqs_sin: [max_len, d_model]
    # cat的原因：保持freqs_sin的前半部分和后半部分存储相同的正弦/余弦值
    freqs_sin = torch.cat([torch.sin(freqs),torch.sin(freqs)],dim=-1)
    freqs_cos = torch.cat([torch.cos(freqs),torch.cos(freqs)],dim=-1)
    return freqs_sin,freqs_cos

def apply_rope(q,k,freqs_sin,freqs_cos):
    """
    应用旋转位置编码
    参数：
        q: 查询张量，形状为 [batch_size, seq_len, num_heads, head_dim]
        k: 键张量，形状为 [batch_size, seq_len, num_heads, head_dim]
        cos: 预计算的余弦值张量，形状为 [seq_len, head_dim]
        sin: 预计算的正弦值张量，形状为 [seq_len, head_dim]
        position_ids: 可选的位置索引张量，形状为 [seq_len]
    """
    def rotate_half(x):
        # 假设q的最后一个维度是2d，这里（x_i,x_i+d)是共享同一个旋转角度的向量对
        # RoPE介绍是相邻旋转,（x_i,x_i+1)一对，本质一样，都可以实现Rope的核心思想
        x1,x2= x[...,:x.shape[-1]//2], x[...,x.shape[-1]//2:]
        return torch.cat([-x2,x1],dim=-1)

    batch_size, seq_len, _, _ = q.shape
    # 截取前 seq_len 个位置的余弦值
    cos = cos[:seq_len]
    # 截取前 seq_len 个位置的正弦值
    sin = sin[:seq_len]
    # 调整cos和sin的形状以匹配q和k的广播需求
    cos = cos.unsqueeze(1)  # shape: (seq_len, 1, d_model)
    sin = sin.unsqueeze(1)  # shape: (seq_len, 1, d_model)
    
    # 实现旋转
    q = q * cos + rotate_half(q) * sin
    k = k * cos + rotate_half(k) * sin
    return q,k

2） Attention with Linear Biases（ALiBi）：

ALiBi提出用于提升Transformer的外推性，不向单词embedding中添加位置embedding，而是根据query、key之间的距离给 attention score 加上一个预设好的偏置矩阵（仅需要修改softmax之前的mask矩阵，将偏置矩阵加上去即可，几乎不增加额外开销）。代表模型：BLOOM。