为什么要学习数据结构的算法？

提升问题解决能力

数据结构与算法是解决复杂问题的工具。掌握它们能帮助更高效地分析问题、设计解决方案，并优化代码性能。例如，排序海量数据时，选择合适的算法可将时间从几小时缩短到几分钟。

优化程序效率

不同的数据结构和算法对程序性能影响巨大。例如，搜索数据时，哈希表比遍历数组快得多。理解底层原理能避免写出低效代码，尤其在处理大规模数据时差距更明显。

通过技术面试

大多数科技公司面试会考察算法能力。熟练常见数据结构（如链表、树）和算法（如动态规划）是获得offer的关键。即使日常开发不直接使用，面试中仍需展示这类知识。

理解技术底层逻辑

许多技术（如数据库索引、网络路由）基于特定算法实现。学习数据结构算法能更深入理解这些技术的工作原理，而非仅停留在表面调用API的层面。

培养逻辑思维

算法训练强调抽象思维和逻辑推理。长期练习能提升拆分问题、归纳规律的能力，这种思维模式对编程乃至其他领域的问题解决都有帮助。

学习数据结构和算法的有效方法

理解基本概念

数据结构和算法是计算机科学的核心基础。数据结构是组织和存储数据的方式，算法是解决问题的步骤和逻辑。理解数组、链表、栈、队列、树、图等基本数据结构，以及排序、搜索、动态规划等常见算法是入门的关键。

选择合适的教材和资源

经典教材如《算法导论》和《数据结构与算法分析》是系统学习的理想选择。在线资源如LeetCode、GeeksforGeeks、Coursera和edX提供丰富的教程和练习题。视频课程如MIT的《Introduction to Algorithms》也是很好的补充。

动手实践

理论学习必须结合实践。通过编写代码实现数据结构和算法，可以加深理解。LeetCode和HackerRank等平台提供大量题目，从简单到困难逐步提升。尝试解决实际问题，如优化程序性能或设计高效的数据存储方案。

分析和优化

学习分析算法的时间复杂度和空间复杂度。理解大O表示法，能够评估算法的效率。通过比较不同算法的性能，掌握优化技巧。例如，理解快速排序和归并排序的优缺点及适用场景。

参加竞赛和项目

参加编程竞赛如ACM-ICPC或Google Code Jam可以提升实战能力。在实际项目中应用数据结构和算法，如开发游戏、构建搜索引擎或优化数据库查询，能够巩固知识并积累经验。

持续学习和交流

加入学习社区或论坛，如Stack Overflow或Reddit的编程板块，与他人交流经验和问题。定期复习和总结，保持学习的连贯性。关注最新的算法研究和应用，如机器学习和人工智能中的算法优化。

什么是数据结构        ？

数据结构的概念

数据结构是计算机存储、组织数据的方式，用于高效地访问和修改数据。它定义了数据元素之间的逻辑关系、操作规则以及存储方式，是算法设计的基础。

数据结构的主要类型

1. 线性数据结构

   • 数组：连续内存存储相同类型元素，支持随机访问。
   • 链表：通过指针连接的非连续存储结构，包括单向链表、双向链表等。
   • 栈：后进先出（LIFO）结构，用于函数调用、表达式求值等场景。
   • 队列：先进先出（FIFO）结构，适用于任务调度、缓冲处理等。

2. 非线性数据结构

   • 树：分层结构，如二叉树、AVL树、B树等，用于数据库索引、文件系统等。
   • 图：由顶点和边组成，用于社交网络、路径规划等复杂关系建模。

3. 抽象数据类型（ADT）

   • 哈希表：通过哈希函数实现快速查找，平均时间复杂度为 O(1)。
   • 堆：完全二叉树结构，用于优先队列、堆排序等。

数据结构的核心操作

• 插入：添加新数据到指定位置。
• 删除：移除特定数据元素。
• 查找：检索数据是否存在或定位其位置。
• 遍历：按特定顺序访问所有元素。

应用场景

• 数据库系统：B树、B+树优化磁盘访问。
• 操作系统：队列管理进程调度，栈处理函数调用。
• 人工智能：图结构用于知识表示和神经网络。

示例代码（数组操作）

# 定义并遍历数组
arr = [1, 2, 3, 4]
for element in arr:
    print(element)

算法是什么？

算法的定义

算法是一组明确定义的、有限的步骤，用于解决特定问题或执行特定任务。它类似于烹饪食谱，详细说明从初始状态到期望结果的转换过程。

算法的核心特征

• 输入：算法接受零个或多个输入。
• 输出：至少产生一个明确的结果。
• 确定性：每一步骤必须无歧义，确保相同输入得到相同输出。
• 有限性：必须在有限步骤内终止。
• 可行性：每一步骤可通过基本操作实现。

算法的常见类型

• 排序算法：如快速排序、归并排序，用于数据有序排列。
• 搜索算法：如二分查找，用于在数据集中定位目标。
• 动态规划：解决具有重叠子问题特性的优化问题。
• 贪心算法：通过局部最优选择寻求全局解。

算法的表示方式

• 伪代码：混合自然语言与编程语法，描述逻辑流程。
• 流程图：图形化展示步骤与决策路径。
• 编程语言实现：如Python、C++等具体代码形式。

示例（快速排序伪代码）

def quicksort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quicksort(left) + middle + quicksort(right)

算法的重要性

算法是计算机科学的基础，直接影响程序的效率与资源消耗。例如，排序算法的时间复杂度从O(n²)优化到O(n log n)可大幅提升大规模数据处理速度。

把大象装进冰箱需要几步？这是不是一个算法？

算！！！

好的算法应该具备以下特性：

高效性

高效性体现在算法的时间复杂度和空间复杂度上。优秀的算法应在合理时间内完成任务，且占用较少内存资源。例如，快速排序的时间复杂度为 (O(n \log n))，优于冒泡排序的 (O(n^2))，更适合大规模数据。

正确性

算法必须能够准确解决问题，对所有合法输入产生预期输出。需通过数学证明或充分测试验证其逻辑无误，例如二分查找需确保边界条件处理正确。

可读性

代码应清晰、结构良好，便于他人理解和维护。命名规范、适当注释和模块化设计能提升可读性。例如，使用描述性变量名而非单一字母。

健壮性

算法应能处理异常输入或边缘情况，如空值、极端数值或非法格式。例如，处理用户输入时需验证数据有效性。

可扩展性

设计时需考虑未来需求变化，便于修改或扩展功能。例如，采用松耦合的模块化设计，避免硬编码参数。

通用性

优秀算法应适用于一类问题而非单一场景。例如，动态规划可解决多种优化问题，如背包问题或最短路径。

最优性

在特定问题约束下，算法应尽可能接近理论最优解。例如，Dijkstra 算法解决单源最短路径问题，保证结果最优。

可测试性

算法应易于验证和调试，通过单元测试覆盖各种场景。例如，使用断言检查中间结果，或设计可复现的测试用例。

低资源消耗

除时间空间效率外，还需考虑 CPU、网络或 I/O 等资源的使用。例如，数据库查询算法需减少磁盘访问次数。

适应性

算法应适应不同环境或数据分布，如在线算法需处理实时数据流。例如，机器学习模型需支持增量学习以适应新数据。

简洁性

避免过度设计，用简单方法解决复杂问题。例如，贪心算法在某些场景下能以较少步骤获得满意解。

时间复杂度定义

时间复杂度用于衡量算法执行时间随输入规模增长的变化趋势，通常用大O符号（O）表示。它描述算法在最坏情况下的运行时间上限，忽略常数项和低阶项。

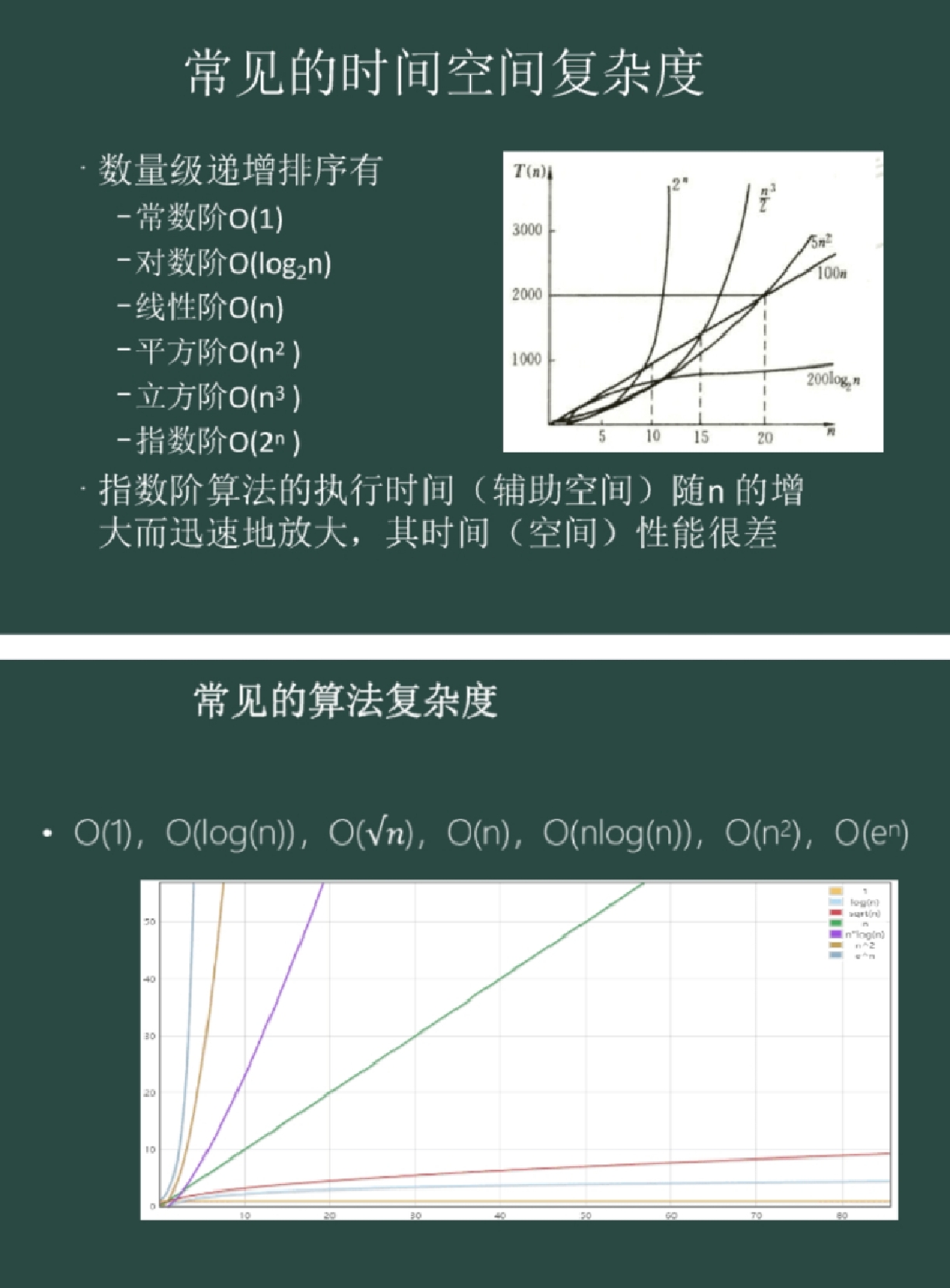
常见时间复杂度类型

1. O(1) 常数时间
   操作时间与输入规模无关。例如：访问数组元素、哈希表查询。

   def get_first_element(arr):
       return arr[0]  # 无论arr多大，执行时间相同
   

2. O(log n) 对数时间
   通常出现在分治算法中，如二分查找。每次操作将问题规模减半。

   def binary_search(arr, target):
       left, right = 0, len(arr) - 1
       while left <= right:
           mid = (left + right) // 2
           if arr[mid] == target:
               return mid
           elif arr[mid] < target:
               left = mid + 1
           else:
               right = mid - 1
   

3. O(n) 线性时间
   执行时间与输入规模成正比。例如：遍历数组或链表。

   def linear_search(arr, target):
       for i in range(len(arr)):
           if arr[i] == target:
               return i
   

4. O(n log n) 线性对数时间
   常见于高效排序算法，如快速排序、归并排序。

   def merge_sort(arr):
       if len(arr) <= 1:
           return arr
       mid = len(arr) // 2
       left = merge_sort(arr[:mid])
       right = merge_sort(arr[mid:])
       return merge(left, right)  # merge操作时间为O(n)
   

5. O(n²) 平方时间
   常见于嵌套循环，如冒泡排序、选择排序。

   def bubble_sort(arr):
       n = len(arr)
       for i in range(n):
           for j in range(0, n-i-1):
               if arr[j] > arr[j+1]:
                   arr[j], arr[j+1] = arr[j+1], arr[j]
   

6. O(2^n) 指数时间
   常见于穷举算法，如斐波那契数列的递归实现。

   def fibonacci(n):
       if n <= 1:
           return n
       return fibonacci(n-1) + fibonacci(n-2)
   

分析方法

• 循环次数：统计嵌套循环的层数。单层循环通常为O(n)，双层为O(n²)。
• 递归调用：分析递归树的分支数和深度。例如斐波那契递归为O(2^n)。
• 主定理（Master Theorem）：适用于分治算法的时间复杂度分析，形式为T(n) = aT(n/b) + f(n)。

优化建议

1. 减少嵌套循环层数，尝试用哈希表（O(1)）替代遍历（O(n)）。
2. 对有序数据优先考虑二分查找（O(log n)）。
3. 避免递归中的重复计算，如用动态规划优化斐波那契问题至O(n)。

通过合理选择算法和数据结构，可显著降低时间复杂度。例如，排序算法从O(n²)优化到O(n log n)能极大提升大规模数据处理的效率。

时间效率分析

关键绩效指标（KPI）追踪
设定可量化的目标（如任务完成时间、项目里程碑），通过工具记录实际耗时与预期对比。常用工具包括Toggl、Clockify或Excel表格，定期复盘偏差原因。

时间日志记录法
详细记录每日活动及耗时，持续至少一周。分类统计工作、学习、休闲等场景的时间分配比例，识别低效时段或重复性耗时任务。推荐使用ATracker或手动记录模板。

帕累托分析（80/20法则）
统计任务耗时与产出价值的关系，筛选出20%高价值活动。优先优化这部分任务的执行流程，削减或委托剩余80%低效工作。

技术辅助工具

自动化跟踪软件
RescueTime自动记录应用和网站使用时长，生成效率报告；ManicTime适用于深度分析本地软件操作行为。

项目管理集成
将时间数据与Jira、Asana等工具关联，分析任务预估与实际耗时的差异。通过甘特图或燃尽图可视化进度瓶颈。

优化策略

批量处理与时段划分
将同类任务集中处理（如邮件回复、会议安排），减少上下文切换损耗。采用番茄工作法划分专注时段与休息间隔。

流程标准化
对高频任务建立SOP（标准操作流程），通过工具模板化重复步骤。例如使用Zapier自动化数据录入或邮件分类。

中断管理
统计每日被打断次数及原因，设置免扰时段或分批处理请求。物理隔离法（如关闭通知）可降低干扰频率。

• 常见时间复杂度