在本文中,我们通过 beta-binomial 模型介绍贝叶斯推理。这是一个数学上易于处理的模型,可以对结果进行详细分析并直观地理解贝叶斯推理的关键要素。尽管模型本身只适用于简单的应用程序,但它所揭示的想法仍然适用于更复杂的贝叶斯模型。

为了建立理论概念,我们考虑一个示例应用:通过查看主队赢得比赛的百分比来分析英超联赛 (EPL) 中的主场优势,我们称之为主场胜率。我们特意关注 2020-2021 赛季,以使示例更有趣。这个赛季很特别,因为由于 Covid-19 大流行,比赛是在没有观众的情况下进行的,或者出席人数有限。

这篇文章不需要任何统计学的先验知识(既不是贝叶斯也不是频率论者),但它确实假设对基本概率论有扎实的理解。在第一节中,我们对贝叶斯推理框架进行了一般性介绍。在第二部分中,我们研究了 beta-二项式模型。在第三部分,我们使用模型来推断主场赢率。在最后一节中,我们将简要讨论先验,这是贝叶斯模型的一个显着特征。

统计推断的贝叶斯方法

贝叶斯框架在通过概率论量化不确定性方面提供了极大的灵活性。在这个范式中,概率表示对感兴趣事件的确定程度的度量。例如,在雨季,您可能坚信某天会下雨。这种信念可以用下雨事件的概率值来表示。

该框架的核心特性是它提供了一种直观且有原则的方法来在观察数据后更新概率信念。例如,如果在这个雨季起床后,你向窗外望去,发现满天的云朵和街上穿着雨衣的人,增加你最初分配给下雨的概率值是明智的。贝叶斯定理提供了一种执行此类更新的系统方法。

在统计推断的上下文中,我们通常对估计存在不确定性(例如下雨的概率或主队赢得足球比赛的概率)的感兴趣量的值感兴趣。这个量通常被转化为概率分布的参数。然后,我们可以使用贝叶斯框架在给定观察数据的情况下推断此类参数的概率分布。例如,我们稍后会看到,我们可以将主队赢得比赛的概率视为伯努利分布的参数,我们可以通过观察一些比赛的结果来推断。

一般来说,我们用_Θ_表示感兴趣的参数,并通过概率分布表达我们对其值的信念。更具体地说,我们可以将概率陈述 P(Θu003dθ) 视为参数 Θ 的值为 θ 的概率1。此外,我们可以用一个密度函数 p(θ) 来概括这个陈述,它表征了 Θ 上的概率分布。这种分布允许表达我们对参数_before_ _观察数据的信念;_因此,它被称为先验分布。例如,如果我们先验地认为局部优势是足球中的一个重要因素,那么我们将选择一个先验密度,将高概率质量分配给主场获胜概率的高值。

在我们观察到一些数据后,我们用_y_表示,我们需要相应地更新我们的信念。更具体地说,我们需要更新先验分布 p(θ), 以考虑观察到的数据。为此目的,条件概率的概念变得至关重要。我们可以将更新后的分布表示为_p(θ|y)_,它可以理解为以观察数据_y为条件的_Θ_上的分布;这是_观察数据后。因此,它被称为后验分布。

贝叶斯推理的基本思想是使用概率定律推导出将先验_p(θ)_更新为后验_p(θ|y)_的规则。此更新规则称为贝叶斯定理。然而,在研究它之前,我们需要考虑数据2的可能值的概率分布,我们用_Y_表示。也就是说,我们必须为给定参数值的数据指定一个概率分布:P(Yu003dy|Θu003dθ)u003dp(y|θ)。重要的是要注意,当我们将 p(y|θ) 视为 y 的函数时,它必须是 Y 上的有效概率分布,但当视为 θ 的函数时,它被称为 *似然函数 * 这不一定是 Θ 上的概率分布。

现在,给定先验和可能性,我们可以用贝叶斯定理推导出后验:

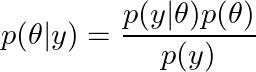
贝叶斯定理:_p(θ)_是先验分布,_p(y|θ)_是似然函数,p(y)是归一化常数,通常称为边际似然。

请注意,贝叶斯定理中的 p(y|θ) 是似然函数(即,它被视为 θ 的函数)。 p(y) 不依赖于 θ,它是后验分布的归一化常数。它被称为边缘似然,因为它是从联合分布 p(y,θ) 中边缘化 Θ 获得的:

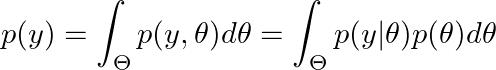
边际似然 p(y) 是通过从联合分布 p(y,θ) 中边缘化 θ 获得的。可以看作是后验分布 p(θ|y) 的归一化常数

一旦我们获得后验,p(θ|y),我们就可以对给定 y 的 Θ 做出任意概率陈述。例如,我们可以考虑参数低于某个值的概率:_P(Θ≤θ|y);_它位于某个区间内的概率:_P(θ1≤Θ≤θ2|y);_甚至找到区间的值,使得该概率等于某个任意值(例如 95%)。

beta-二项式模型

现在我们在 beta-二项式模型中具体化贝叶斯推理的元素。回想一下,作为一个说明性示例,我们有兴趣使用该模型来估计主队在 EPL 中赢得比赛的概率。我们将此概率称为主场获胜率并用_Θ_表示。

模型规范:似然和先验

我们需要在贝叶斯模型中指定的两个关键元素是先验分布和似然函数。然后,我们可以在贝叶斯定理中使用它们来推导后验分布。

通常更容易根据可观察数据来理解参数与它的关系。鉴于此,我们首先指定可能性。在我们的例子中,我们只关心主队是否赢得比赛;因此,我们不需要区分平局和客队获胜。然后,我们可以根据二元结果来考虑每场比赛:主队获胜或不获胜,并将此结果建模为伯努利随机变量,参数 Θ, 代表主队获胜的概率。

但是,数据包含不止一场比赛的结果(一个赛季有 380 场比赛)。然后,我们需要考虑多个伯努利实例的联合结果的可能性。这就是二项分布,它模拟了在 n 场比赛中观察到 y 个主场获胜的概率,前提是每场比赛具有由 θ 给出的相同的主场获胜概率,并且比赛彼此独立。然后,如果表示_n_场比赛中主场获胜次数的随机变量用_Y_表示,则二项分布由下式给出:

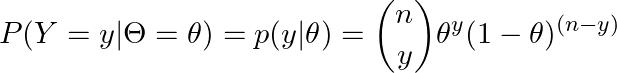
二项分布: 计算在 n 场比赛中观察到 y 个主场获胜的概率,当比赛彼此独立且每场比赛具有相同的主场获胜概率 θ

为了进一步了解 Y 上的二项式分布,下图显示了 Θ 某些特定值的概率质量函数:

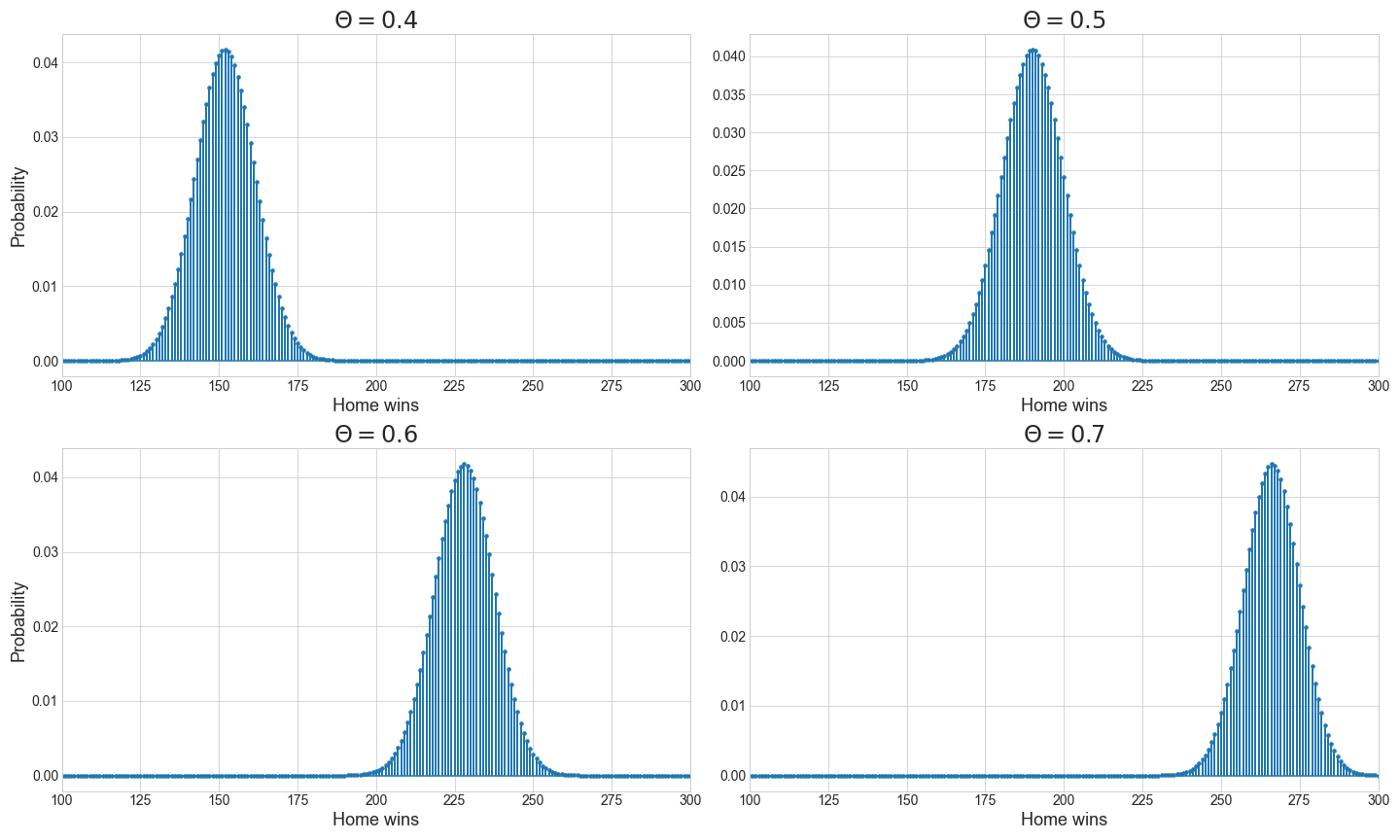
在不同 Θ 值下,家庭获胜示例的二项式分布。数据包含一个赛季的结果,该赛季有 380 场比赛,然后我们固定 nu003d380。图片由作者提供。

为了完成模型规范,我们需要在 Θ 上定义一个先验分布。这可以说是贝叶斯模型中的一个关键选择,因为推理的结果可能对它很敏感。选择先验的指导原则是,它应该作为一种机制,赋予模型我们对手头问题的先验知识。这些知识可能来自不同的来源,例如该主题的专业知识、以前的研究或历史数据。

可能有各种分布族足够灵活,可以表达我们关于参数的特定先验知识。然而,另一个需要考虑的因素是数学上的便利性。在我们的简单示例中,易于处理的模型将提供足够的灵活性来编码广泛的先验信念。特别是 beta 分布是一个不错的选择,因为它提供了灵活性和数学上的易处理性。 Θ 上的 beta 分布由下式给出:

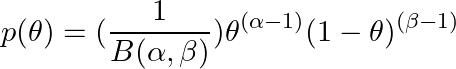
Beta 分布。 我们使用 beta 分布作为 Θ 的先验。它取决于两个参数(α,β),这将决定它的形状并允许对不同的先验信念进行编码。

B(. , .) 是beta 函数可以看作是分布的归一化常数。 α 和 β 是定义分布形状的参数,并且将提供灵活性来表达广泛的先验信念。下面的动画展示了他们是如何实现这一点的:

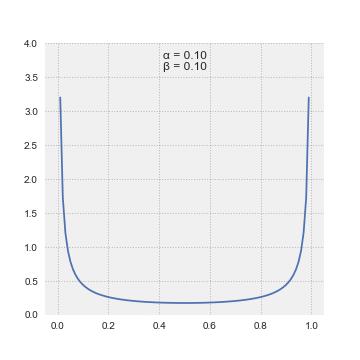
不同α和β值下的β分布。请注意,密度可以采用多种形状,允许对有关参数的各种先验信念进行编码。图片来自 Pabloparsil — 自己的作品,CC BY-SA 4.0,https://commons.wikimedia.org/w/index.php?curidu003d89335966

正如我们将在下一节中更深入地看到的那样,分布的汇总统计有助于设置先验参数的值。在 beta 分布下 Θ 的均值和方差由下式给出:

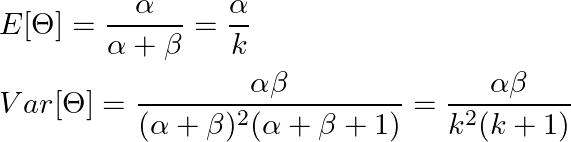
**β分布的均值和方差。**为方便起见,我们定义ku003dα+β,它决定了分布的集中程度。

为方便起见,我们定义了_ku003dα+β_。请注意,k 的方差正在减小,这有时被称为浓度参数3。

后验推导

现在我们已经准备好使用贝叶斯定理推导出后验分布。在这个阶段,使用 beta 先验的数学便利性变得清晰起来。因此,根据贝叶斯定理,我们得到:

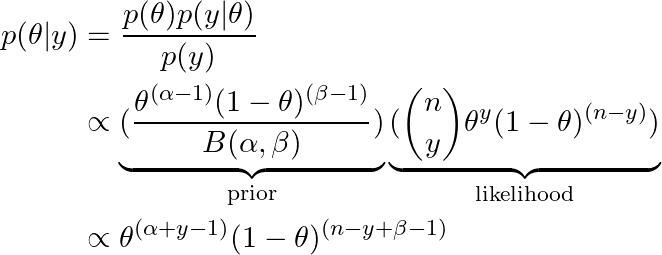
**后验分布的推导。**为清楚起见,在最后一步中,我们删除了不依赖于 θ 的常数项。请注意,后验与类似于 beta 分布的函数形式成比例。

请注意,后验密度与 beta 分布的函数形式成正比。细心的读者会发现,比例常数必须恰好是 beta 归一化常数 (1/B(.,.)),因此,后验本身就是 beta 分布!

为了更清楚地看到这个结果,让 α'u003dα+y 和 β'u003dn-y+β 并注意:

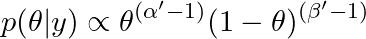
由于后验是一个概率分布,它必须是这样的情况:

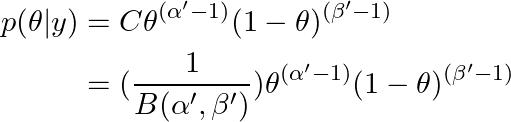
后验是 beta 分布 带有参数 α'u003dα+y 和 β'u003dn-y+β。 归一化常数 C 必须是 beta 归一化常数,因为后验具有β密度的函数形式。

我们已经推断出比例常数 C 必须是 beta 归一化常数,因为后验共享 beta 分布的函数形式,直到一个必须确保它积分为 1 的常数(即归一化常数)。

现在,β-二项式模型的数学便利性是显而易见的:只要我们有一个 beta 先验和二项似然,后验分布也将是 beta,参数为 α'u003dα+y 和 β'u003dn-y+β。在这种情况下,我们说先验分布与可能性是共轭的。

在后验分布中,我们可以找到先验知识和数据之间的权衡。为了注意这一点,我们检查后验均值:

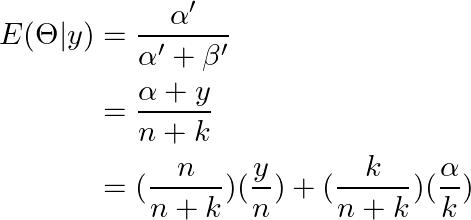
后验平均值是数据速率 (y/n) 和先验平均值 (α/k) 之间的加权平均值。权重由n和k决定:如果n>k,则数据权重较大,如果k>n,则先验权重较大。

请注意,后验均值表示数据和先验之间的折衷。特别地,后验均值是数据速率 (y/n) 和先验均值 (α/k) 的加权平均值,其中权重由 n 和 k 确定。如果_n>k_,则数据的权重将大于先验,反之亦然,则先验的权重会更大。

以这种方式查看后验均值可以直观地解释先验参数:我们可以将 k 视为先验样本大小,即告知我们先验信念的匹配数,或者等效地,我们需要匹配的数观察数据,使其具有比先验知识更强的权重。同样,我们可以将_α_视为先前主场获胜的次数。也就是说,在之前的 k 场比赛中,α 场都是主场获胜。因此,先验平均值 α/k, 可以解释为先验主场胜率。类似地,β 可以被认为是主队没有获胜的先前比赛次数。

主场胜率推断

最后,我们使用 beta-binomial 模型来推断 2020-2021 赛季 EPL 的主场获胜概率。为此,我们使用了本赛季 380 场比赛结果的数据(数据在Kaggle上公开,由@Alvin提供)。本赛季的一个重要怪癖是它发生在 Covid-19 大流行期间,因此大多数比赛都是在没有公开或出席人数有限的情况下进行的,这显然会影响主场获胜率。这个例子的目的是纯粹的教学,因为它是一个真实的例子,非常适合展示 beta-binomial 模型和贝叶斯推理的主要思想。

在推导后验之前,我们需要设置先验参数_α_和_β_的值。一种方法是使用历史信息。我们知道,在前五个赛季(2015-2016 到 2019-2020)的 1900 场比赛中,主场胜率为 0.46。那么,我们可以将 0.46 视为之前的主场胜率。回想一下,我们可以将 ku003dα+β 解释为先验样本量。在这种情况下,它可以被认为是告知我们先验知识的匹配数量。因此,一个明智的选择是设置 ku003d1900,这是我们正在考虑将先前主场胜率设置为 0.46 的历史比赛数。由于 α 是先前主场获胜的次数,我们将其设置为 αu003d0.46*ku003d874。最后,这意味着_βu003dk-αu003d1026_。

关于似然性,我们固定 nu003d380,即 2020-2021 赛季观测数据中的比赛场数,观测到的主场胜场数为 yu003d144。那么数据主场胜率为_y/nu003d0.38._

现在,我们已经完全指定了我们的模型,我们可以推导出后验分布。如上一节所述,后验也是一个β,参数为_α'u003dα+yu003d1018_和_β'u003dn-y+βu003d1262_。下图显示了模型的可视化:

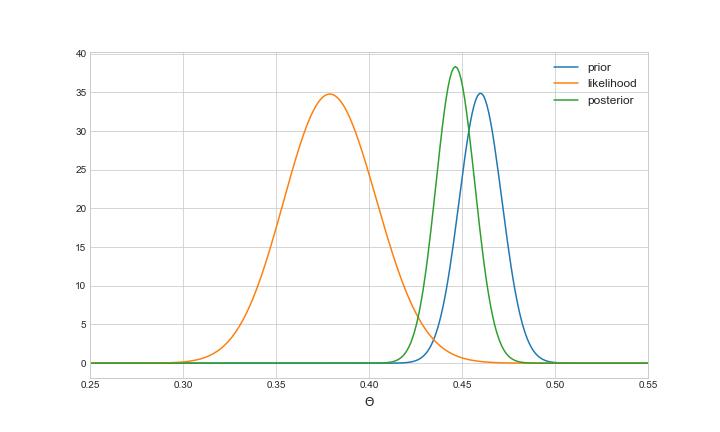
具有先验参数 αu003d874 和 βu003d1026 的模型。对可能性进行缩放以进行更清晰的可视化。由于k>n,后验倾向于先验。然而,数据(通过可能性)在后验中仍然有明显的影响。图片由作者提供。

请注意,正如我们在上一节中所解释的,后验分布是先验和似然之间的折衷。由于在这种情况下,我们设置_ku003d1900>380u003dn_,先验比似然更集中,对后验的影响更大。然而,这种可能性在将后验移向 0.38 的数据本垒打获胜方面仍然具有显着影响。

我们可以使用派生的后验来获得任意概率查询的结果。例如,我们可以找到主场胜率的中心95%概率区间(也称为可信区间),由_(0.426, 0.466)_给出,如下图所示:

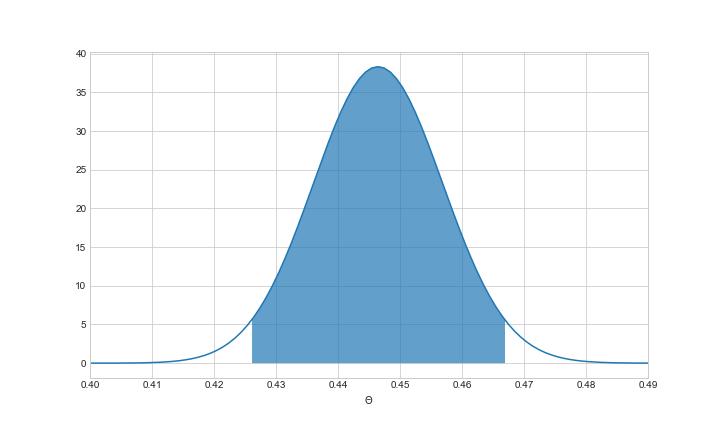
** Θ 的后验 95% 概率中心区间为 (0.426, 0.466)**。它包括0.46的先前主场胜率,但不包括0.38的数据主场胜率。图片由作者提供。

给定数据,我们还可以问,主场胜率低于历史数据 0.46 的概率是多少。答案是 0.90,如下所示:

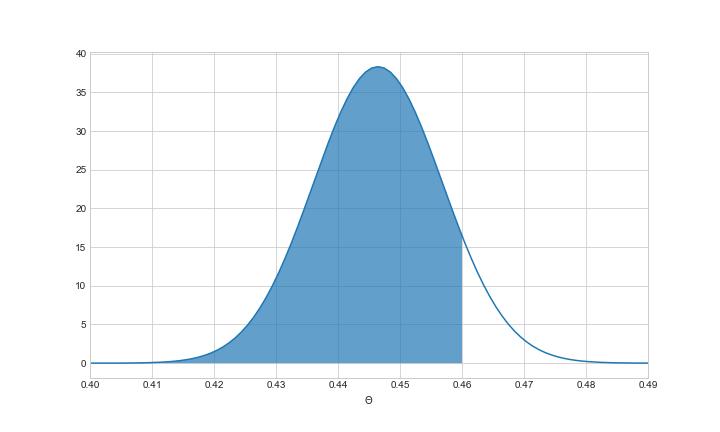
主场胜率低于0.46的后验概率为90%。图片由作者提供。

现在,一个合理的论点是,我们的先验过于自信,因为我们是在对参加人数有限的比赛的赛季进行推断,而我们的先验主要是根据大流行之前的赛季进行的。然后,如果我们有兴趣评估大流行季节期间的主场获胜率,那么降低我们对这种先前信念的信心是明智的。通常,贝叶斯数据分析中的讨论围绕先验的选择展开,因此正确证明该决定的合理性很重要。此外,评估所获得的结果对不同先验参数值的敏感程度是一个很好的做法。

鉴于上述论点,我们考虑了一个先验不自信的替代模型。如上一节所示,表达这一点的一种方法是减少先验样本大小_k_。例如,假设我们想将其减少到我们对先验和数据赋予相同权重的程度。然后,我们应该设置_ku003dnu003d380_。如下图所示,这将导致数据和先验在后验均值中的权重相等:

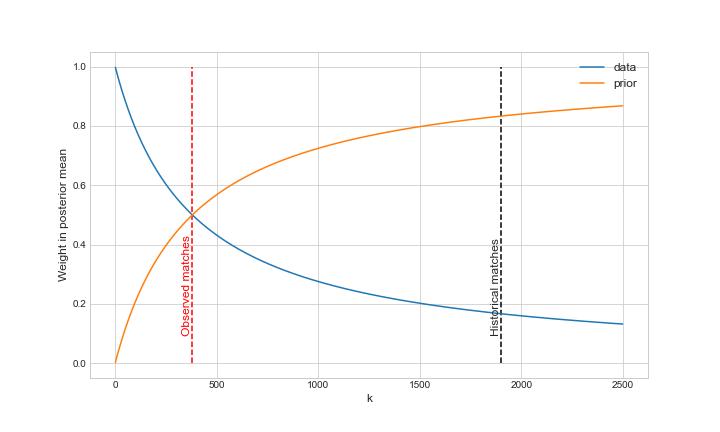
数据的权重和后验平均值中的先验 针对不同的 k 值。如果我们将 k 设置为历史匹配数(1900 次),则先验均值将主导数据。如果我们设置 ku003dnu003d380,则权重相等。

如果我们继续这个策略并保持_0.46_的先验主场赢率,我们得到以下先验参数值:_αu003d175_和_βu003d205._然后,得到的后验参数是α'u003d319和β'u003d 441如下图所示:

! zoz100077](https://devpress-image.s3.cn-north-1.jdcloud-oss.com/a/a15a7edcc3_1*6fyFlvDGR7MYUT6E-S0Wyg.jpg)

具有先验参数 α u003d 175 和 βu003d205 的模型。在这种情况下,选择 k 使得先验和数据在后验均值中具有相同的权重。后验均值恰好是最大似然 (y/nu003d0.37) 和先验均值 (α/ku003d0.46) 之间的中点。

在这种情况下,后验位于先验均值 α/k, 和数据速率 y/n, 之间的中点,这也是最大似然点。在这种情况下,95% 的后验可信区间为 (0.385, 0.455),它仍然不包括观察到的 0.38 的主场获胜率,但现在它也不包括 0.46 的先验率。在这个模型规范下,主场胜率低于历史值 0.46 的概率现在接近 99%。因此,确实结果对先验参数很敏感。

现在,一个更极端的批评者可能会争辩说我们应该完全放弃我们的先验知识,因为它根本不适用于我们正在考虑的季节4。这位批评家可能会要求我们“让数据自己说话”的更“客观”的分析。这种设置也可以用贝叶斯框架建模,当我们没有任何关于手头问题的可靠先验信息时,这可能是一个明智的选择。

使用具有最少信息的先验(也称为无信息先验或平坦先验)的一种方法是选择一个分布,该分布为 _Θ 的每个可行值分配相等的密度。在这种情况下,我们可以在区间 [ 0,1]。幸运的是,β-二项式模型足够灵活,可以涵盖此设置,因为当 αu003dβu003d1 时,均匀分布是 beta 的一种特殊情况。在这种情况下,我们得到 α'u003d145 和 β'u003d237 的 beta 后验,如下图所示:

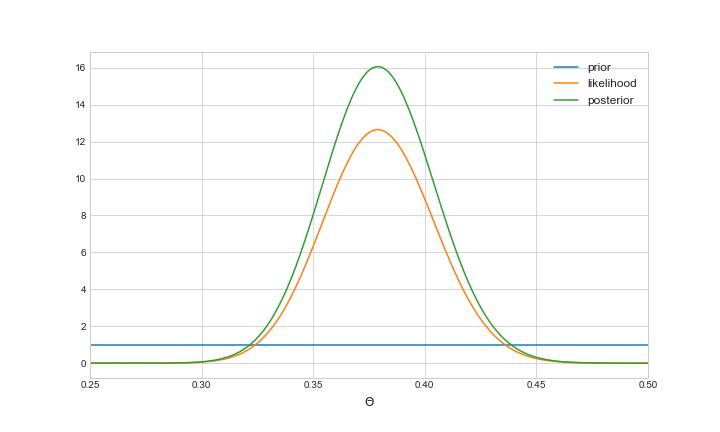
具有无信息先验的模型 (αu003dβu003d1)。 在这种情况下,后验只是可能性的缩放版本。数据完全支配先验。

在这种情况下,后验只是可能性的缩放版本。特别是,后验模式(称为最大后验的点估计)与最大似然点重合(即数据速率_y/nu003d0.38_)。更明确地说,最大化似然性的 Θ 的值也最大化后验密度,这个值是数据速率,y/n,,通常称为最大似然估计5。不出所料,此设置提供了更加明显的结果:95% 的可信区间现在为 (0.332, 0.429),其中包含观察到的 0.38 的主场赢率,不包括 0.46 的历史数据。此外,主场胜率低于历史值的概率接近1。下表总结了模型三种不同设置下得到的结果:

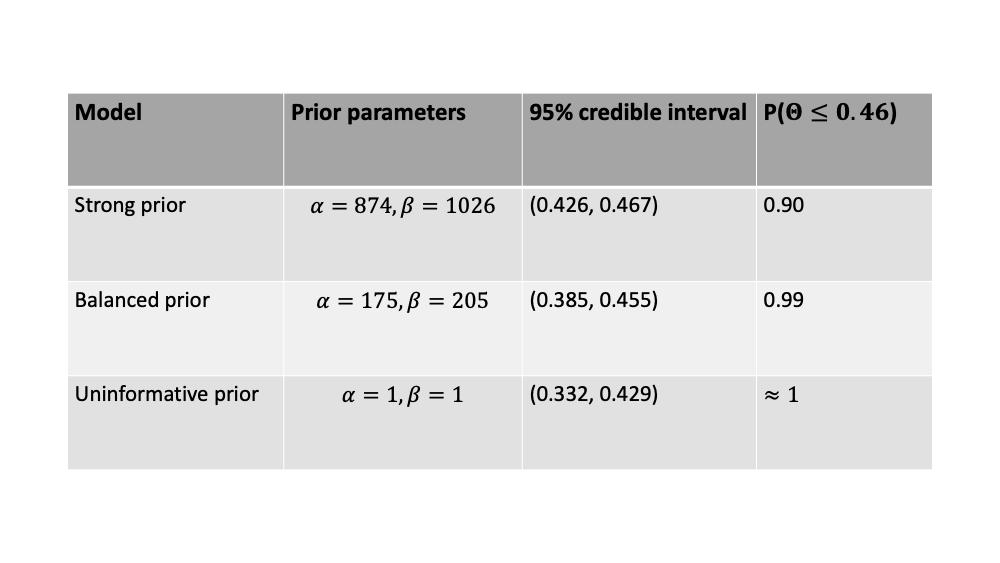
不同型号规格下的结果。结果显然对先验参数的选择很敏感。

先验浅谈

先验是贝叶斯推理的一个显着特征。先验的选择本质上是主观的,如上例所示,它会对模型的结果产生重大影响。起初这可能看起来令人不安,并且使用信息量不足的先验似乎是最客观的方法。然而,更仔细的研究表明,这种选择也不是没有假设的。而且,在某些情况下,它甚至可能涉及一个非常强大的!例如,在主场优势示例中,使用无信息先验的一个含义是,来自前几个赛季的信息被认为与估计主场获胜率完全无关。只有在特殊情况下,如大流行病,才能证明如此强大的主张是合理的。

更一般地说,只要我们有关于手头问题的可靠信息并且它不包含在数据中,我们就应该在先验中对其进行编码。先验不一定会引入尚未存在的假设,它只是将它们明确化。因此,如果使用得当,它应该被视为贝叶斯框架的优势,而不是劣势。总而言之,它可以让模型背后的假设更加透明。

重现示例的代码位于:https://github.com/Romoflow/beta-binomial/blob/master/model.ipynb

示例中使用的数据位于:https://www.kaggle.com/datasets/irkaal/english-premier-league-results

脚注

1. 这个陈述在频率论方法中没有意义,因为它将参数视为固定值而不是随机变量。^

2. 在这种情况下,我们使用大写的 Y 来区分数据作为一个随机变量,它可能与我们观察到的实际数据(我们用 y, 表示)取不同的可能值,因为它是 Y 的值。^

3. 有关浓度的更详细说明,请参阅 John Kruschke 的_done__ Bayesian Data Analysis_。^

4. 这可能太极端了,因为 2019-2020 赛季的一些比赛,这是我们历史信息的一部分,由于大流行已经在没有观众的情况下进行。此外,在某些赛季有几场比赛没有上场的情况并不少见。然而,出于教学目的,我们接受这一论点。^

5. 找到最大化似然性的值并将其用作参数的点估计是频率论范式中的常用方法。^

延伸阅读

Kruschke, J. K. (2011)。 Doing Bayesian data analysis: A tutorial with R and BUGS. Elsevier Academic Press。

Gelman, A.、Carlin, J. B.、Stern, H. S. 和 Rubin, D. B. (1995)。 贝叶斯数据分析。查普曼和霍尔/CRC。