大模型相关论文（科学趋近于真理）：The Platonic Representation Hypothesis

一、摘要

  • 我们认为，AI模型（尤其是深度神经网络）中的表示正在趋同。首先，我们在文献中回顾了大量趋同的案例：随着时间的推移，在多个领域中，不同神经网络表示数据的方式正变得越来越一致。接着，我们展示了跨模态数据的趋同现象：例如，随着视觉模型和语言模型的规模变大，它们在衡量数据点之间距离的方式上也越来越相似。我们假设这种趋同正朝着一个共享的统计现实模型演化，这类似于柏拉图关于理想现实的概念。我们称这种表示为柏拉图式表示，并讨论了多种可能促使其出现的“选择性压力”。最后，我们讨论了这些趋势的意义、它们的局限性，以及对我们分析的反例。

二、介绍

  • AI 正在从“特定任务专用模型”走向“通用多任务模型”，从“模态隔离”走向“模态统一”。这意味着未来的AI系统不仅可以同时处理文本、图像、语音等，还能在架构层面共用同一网络结构或表示空间。这直接推动了一个现象：不同模型的表示空间变得越来越相似。例如，过去需要为不同的语言处理任务（如情感分析、句法分析、对话）构建专门的解决方案；而现在的**大型语言模型（LLMs）**可以用同一组参数胜任所有这些任务。
  • 表示趋同（Representational Convergence）：指不同模型对数据（如句子、图像）的向量化表示越来越相似，不论其架构或训练任务是否相同。
  • 柏拉图式表示（Platonic Representation）：一种理想的、统计意义上的“真实世界的表示”。所有神经网络似乎都在逼近这种表示。
  • 该概念借用了哲学比喻：模型训练数据是“影子”，真正的现实是“洞外的世界”，模型训练的过程就是通过影子“反推出现实”。
  • 源自小说《安娜·卡列尼娜》开头那句名言：“幸福的家庭都是相似的，不幸的家庭各有不同。”。Bansal 等人借用这个隐喻来表达：所有表现良好的模型在表示世界的方式上是趋同的。这意味着只要模型性能好，它就一定在表示空间中学到了类似的结构。
  • 本文的中心论点是：AI模型的目标不是在“任务表现”上多样化，而是在“现实建模”上趋同。换句话说，最强的模型必然在某种形式上反映了同一个现实世界的统计结构。

下图为柏拉图假设的直观展示：

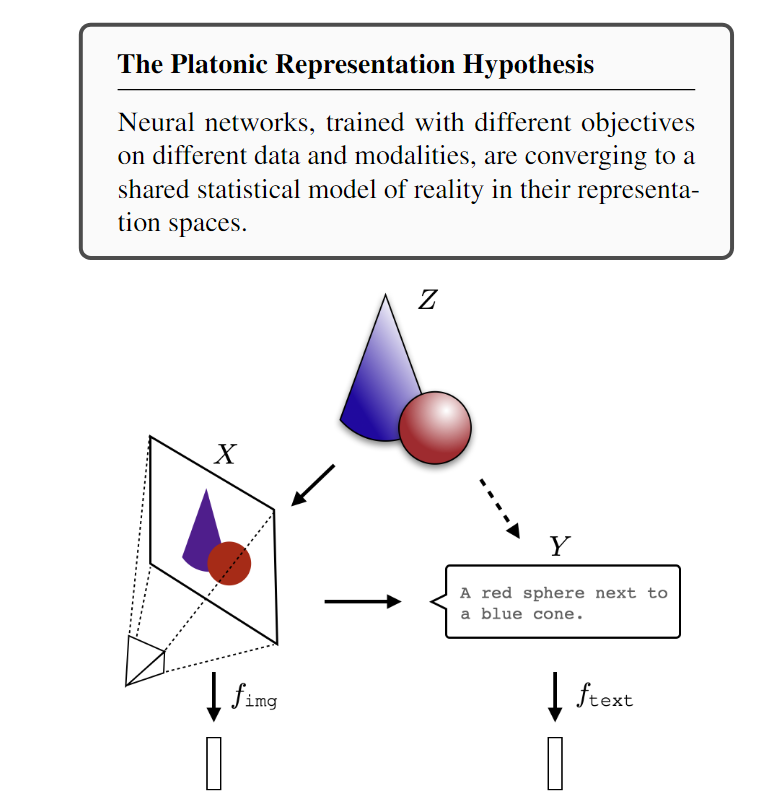
在这里插入图片描述

  • Z（中心位置）：现实世界的底层真实状态（underlying reality），即“柏拉图式真理”

  • X（左下图像）：图像模态的观察结果，例如用相机拍到的一张照片

  • Y（右下文字）：语言模态的观察结果，例如对图片的文字描述

  • fimgf_{img}fimg​/ ftextf_{text}ftext​（下方柱状图）：图像模型或语言模型对 X / Y 的表示向量（embedding）

  • 实箭头：从真实世界 Z 到某一模态的直接观测或推断

  • 虚线箭头：间接生成的投影，例如从图像 X 生成文本描述 Y

  • 假设是：虽然这两个模态（X 和 Y）看似差异巨大，但它们本质上都源自同一个底层现实 Z，因此其最终表示会越来越接近。

  • 哲学思想（柏拉图的洞穴）：

    • 现实（Z）：洞穴外的真实世界；
    • 图像（X）和语言（Y）：是洞穴墙上的影子，是不完整的感知；
    • 模型学习的过程：是AI试图通过这些影子重建“洞外的真实”；
    • 最终收敛的表示：即 Platonic Representation，是所有感知系统逐渐逼近的那个“理想表示”。

三、表示正在收敛

  • 本文提出用“核函数 + 对齐度量”来形式化地衡量不同模型之间是否对数据具有相似的表示结构。举个例子：
    • 模型A和模型B都接收到相同的100张图片；
    • 它们各自生成100个嵌入向量；
    • 用内积矩阵 KKK 表示这些嵌入之间的相似性；
    • 如果A和B的内积矩阵很接近，说明它们的表示方式是趋同的。

3.1 具有不同架构和目标的不同模型可以对齐表示

  • 即使神经网络在架构、训练目标、任务范式（监督 / 自监督）都不同，它们在训练过程中仍然能学习出高度相似的表示结构，即使是中间层的表示。
相关研究
  • Lenc 等人的工作：用ImageNet模型的前几层接上Places365模型的后几层仍能维持良好性能；说明表示对齐主要发生在中间或早期层。
  • Moschella等人的工作：用零样本拼接（zero-shot stitching）将语言模型和视觉模型拼接；成功地在不同模态间共享中间表示。
  • Dravid的等人提出“Rosetta Neurons”，即多个模型中自动学到相同功能的神经元。
举例
  • 将一个用英文训练的编码器连接到用法文训练的解码器，居然仍然能生成合理句子；
  • 在自监督模型和监督模型之间拼接结构，性能无损。
  • 在多种架构、多种任务、多种初始化中，仍然存在某种“吸引点”或共同结构，模型倾向于收敛到这一结构上。

架构、任务不是决定表示的全部，训练过程中，模型趋向于找到一种共同、稳定、任务泛化的真实世界结构表示方式。

3.2 对齐随着模型规模和性能的增加而增加

  • 随着神经网络变得更大、更深，能够处理更多数据、更复杂任务时，它们所学习到的表示不仅更强大，而且也更加一致。
相关研究
  • Kornblith et al. (2019)：提出CKA度量并发现规模大模型表示更对齐；
  • Roeder et al. (2021)：在CIFAR-10等数据集上验证模型间对齐随性能提升；
  • Balestriero & Baraniuk (2018)：理论上指出高性能模型的激活模式趋同。
相关实验
  • 本文评估了78个视觉模型在 VTAB 数据集的迁移性能；将模型按性能分组，比较组内平均对齐度；结果表明高性能组对齐度显著更高，表示更集中，低性能组表示更分散，这表明语言模型与视觉模型在表示空间中是可以对齐的，而且这种对齐程度是可量化的。具体实验如下：

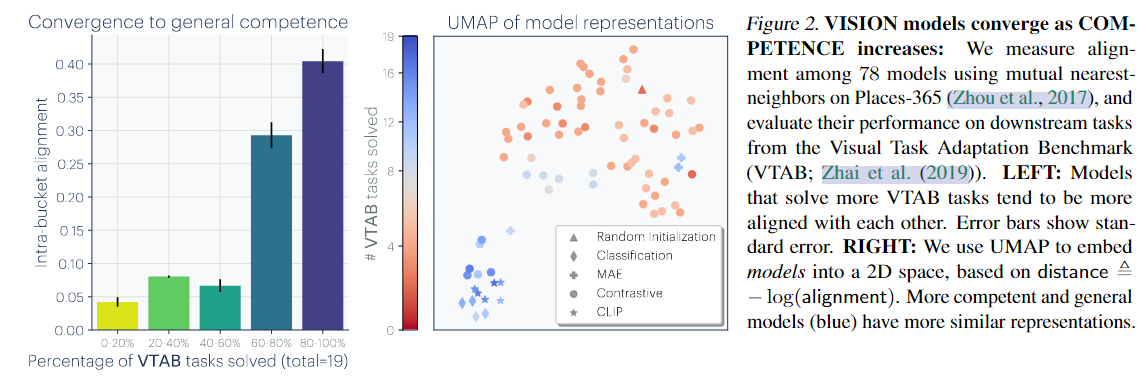
在这里插入图片描述

左图表明模型能力越强，其表示对齐度越高。右图表明更相近的模型在低维空间中聚类

  • 可以将每个视觉模型比作一个“观察现实世界”的人：
    • 能力弱的人（低 VTAB 得分）各说各话，看不清世界，理解方式五花八门；
    • 能力强的人（高 VTAB 得分）看到的事物更加一致，表达方式也趋向统一；

3.3 跨模态表示也在统一收敛

  • 表示趋近于统一不仅存在于单模态系统中，跨模态的深度模型（如图像与文本）也表现出强烈的表示对齐趋势。这意味着，不同感知系统（视觉、语言、声音）训练出的模型，在高层嵌入空间中也会逐渐靠近，甚至可以共享表示空间。研究者发现，仅使用一个简单的线性映射，就能把视觉模型输出的特征接入语言模型，完成诸如图像问答、图像字幕等任务。
  • 这一现象不仅限于视觉与语言，像声音（语音识别）、面部表情、动作轨迹等模态，也能通过特定的映射方式与LLM建立有效连接。这种多模态表示的统一收敛趋势，标志着AI系统正逐步形成一个跨感官、跨任务、统一表示的认知系统。

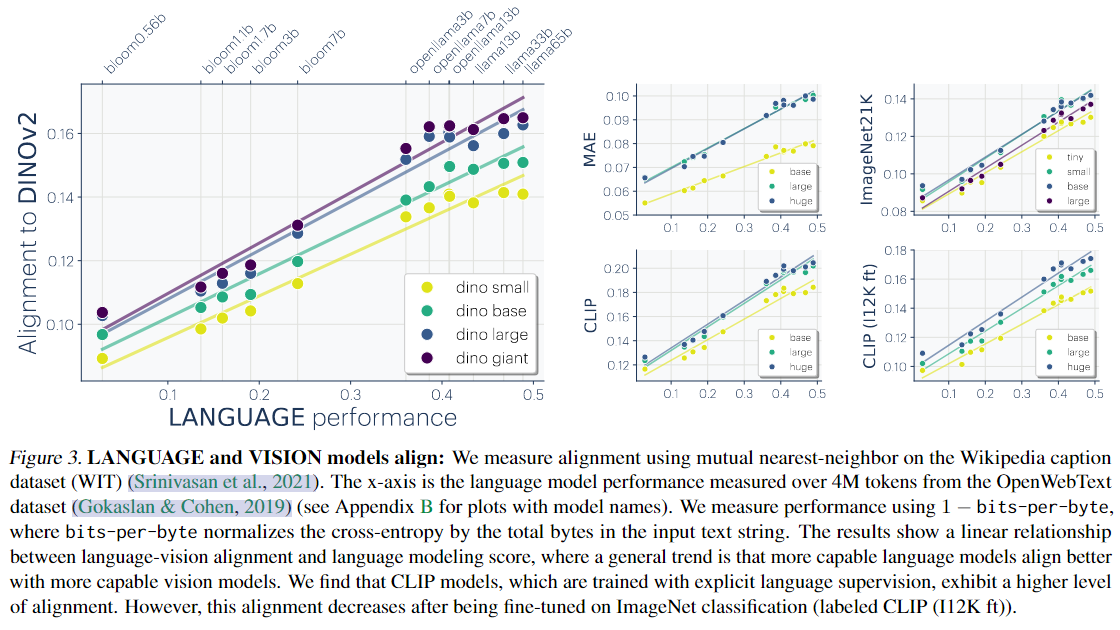
在这里插入图片描述

  • 语言性能越高 → 越容易对齐视觉模型：语言模型的表示空间更语义化、抽象，接近图像语义结构。
  • 视觉模型越大 → 越容易与语言模型对齐：视觉模型也需具备足够复杂的结构能力才能对齐。
  • 训练范式影响对齐结构：
    • CLIP这种语言监督训练方式对齐度最高；
    • CLIP微调为分类任务后会“破坏”表示的通用性，使得语言对齐能力下降。

3.4 模型的表示结构正在接近生物大脑

  • 神经网络不仅与彼此对齐，其表示空间结构甚至与人类大脑的神经活动模式惊人相似。
  • 早在2014年，Yamins等人就已通过实验发现，CNN对图像的激活反应与灵长类视觉皮层的神经元活动高度一致，尤其在高层视觉任务上。后续研究表明，大脑和深度模型都倾向于使用稀疏编码、边缘检测、对象识别等策略来构建信息表示，这些是认知系统处理图像信息的基本机制。
  • 大脑与AI虽在物理实现上截然不同，但在对现实结构的建模方式上，存在深层次的收敛。

3.5 表示对齐是否能提升下游性能？

  • 通过一系列实验证明，表示对齐一般意味着模型泛化能力更强、任务表现更好
  • 模型表示的对齐程度越高，它在多个下游任务上的表现也越好。本文选取了诸如 HellaSwag（常识推理）和 GSM8K（数学问题）等任务进行评估，发现随着表示对齐度的提高，模型在这些任务中的准确率、鲁棒性、泛化能力均有提升。
  • 这一发现具有极其重要的意义：它说明表示收敛不仅是训练过程中的“副产物”，而是与模型性能直接相关的因素。可以说，一个模型的泛化能力，部分来源于它是否学到了和其他优秀模型相似的世界表示。这也解释了为什么越来越多的顶级模型采用通用预训练结构作为骨干网络，并倾向于对输入数据进行统一编码。最终的目标，不只是优化某一任务，而是逼近世界的真实结构。

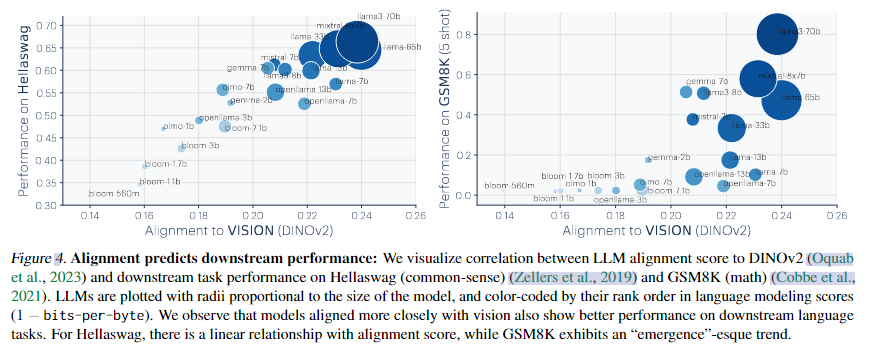
在这里插入图片描述

  • 上图展示了大型语言模型（LLM）与视觉模型 DINOv2 的对齐程度与下游任务性能之间的关系。
  • 在 HellaSwag（常识推理）任务中，对齐程度越高，性能越好，呈现线性提升趋势。
  • 在 GSM8K（数学推理）任务中，随着对齐程度增加，性能在某一阈值后出现突跃式提升（emergence 现象）。
  • 说明：LLM 与视觉模型对齐得越好，语言和推理能力也越强。

四、为什么表示会收敛

  • 现代机器学习模型通常被训练来最小化经验风险，并可能包含隐式或显式的正则化。公式为：

f∗=arg⁡min⁡f∈FEx∼dataset[L(f,x)]+R(f)f^* = \arg\min_{f \in \mathcal{F}} \mathbb{E}_{x\sim dataset}[\mathcal{L}(f,x)] + \mathcal{R}(f)f∗=argf∈Fmin​Ex∼dataset​[L(f,x)]+R(f)

  • 其中，$\mathcal{F} 表示函数类，表示函数类，表示函数类，\mathcal{L} 表示训练目标，表示训练目标，表示训练目标，\mathcal{R}$ 表示正则化。

  • 接下来讨论公式中各部分如何促进表示收敛。

4.1 通过任务广义性（Task Generality）的收敛

  • 每一个训练样本和任务目标都会对模型施加一个约束。随着数据量和任务数量的增加，能够同时满足所有约束的表示空间会逐渐缩小。因此，当模型需要同时解决更多任务时，可能的表示解空间会减少，从而更容易收敛。

  • **多任务扩展假设（The Multitask Scaling Hypothesis）：**能胜任 N 个任务的表示，比能胜任 M (<N) 个任务的表示更少。换句话说，模型越通用，它的可行解越少，表示也越收敛。

  • 这一点也可以从“反协方差原则（Contravariance principle）”理解：简单目标的解集很大，而复杂目标的解集相对较小。当我们增加数据规模时，模型从经验风险的优化会更接近真实分布，从而更好地捕捉世界的统计结构，解空间进一步收窄。

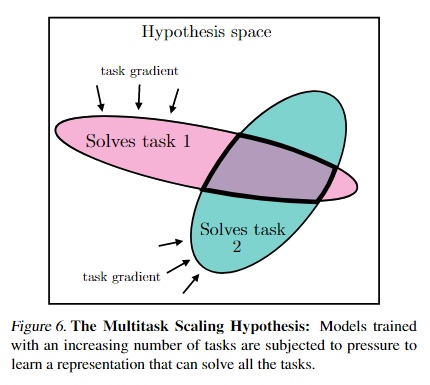
在这里插入图片描述

  • 图中展示了在同一个假设空间内，不同任务的“解空间”：
    • 粉色区域：能解决任务 1 的假设集合。
    • 蓝色区域：能解决任务 2 的假设集合。
    • 重叠部分（紫色）：能同时解决两个任务的模型表示。
      随着任务数量增多，要找到能同时解决所有任务的解会变得更难，重叠区域变得更小。
  • 即：当模型需要解决更多任务时（例如从 M 个扩展到 N 个，且 N > M），能同时胜任这些任务的表示数量会减少，因此模型会被迫学习到更通用、更共享的表示。当模型同时学习更多任务时，它会受到“任务梯度”的共同约束，被迫学习一个能兼顾多个任务的统一表示。

4.2 通过模型容量（Model Capacity）的收敛

假设存在一个“全局最优表示”，能够在标准学习目标下达到最好效果。那么在数据充足的情况下：

  • 更大的模型（函数类更大 F\mathcal{F}F）、更好的优化方法，能更接近这个全局最优表示；

  • 即便架构不同，大模型在相同任务目标下，也会逐渐收敛到类似解。

  • 容量假设（The Capacity Hypothesis）： 更大的模型比小模型更有可能收敛到共享的表示，因为它们能够探索更广阔的函数空间，并在其中找到更优的共同解。

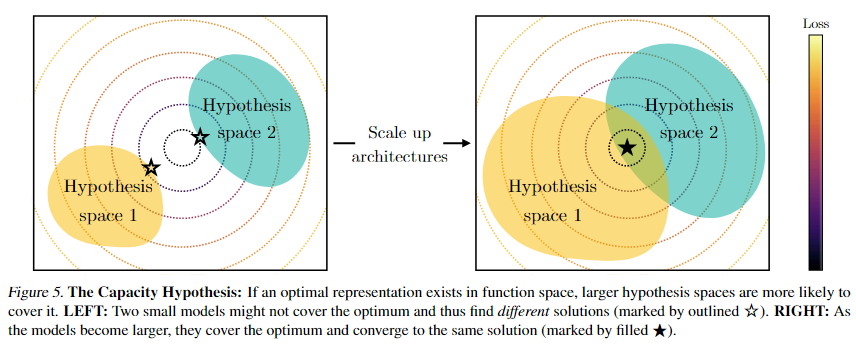
在这里插入图片描述

  • 上图说明当存在一个真正“最优的表示”（optimal representation）时，模型容量越大（即假设空间越广），越有可能包含并学习到这个最优解。小模型可能因为容量限制而学到不同、次优的解。大模型因为覆盖范围更广，更容易收敛到同一个更优的全局表示。

4.3 通过简约偏置（Simplicity Bias）的收敛

  • 虽然模型可能通过不同的方式实现相同的训练效果，但为什么不走复杂的路径，而是收敛到相似的解？一个关键原因是：深度网络天然有简约偏置。

  • **简约偏置假设（The Simplicity Bias Hypothesis）：**深度网络倾向于选择简单的函数拟合数据，而不是过度复杂的方案。模型越大，这种偏置越强。因此，模型规模扩大后，可能的解空间反而更小，表示更趋同。

  • 这种简约偏置可能来自：

    • 显式正则化（如权重衰减、dropout），强制模型选择更简单的解；
    • 但即使没有正则化，深度网络也遵循“奥卡姆剃刀”：隐式地偏向能解释数据的简单方案。

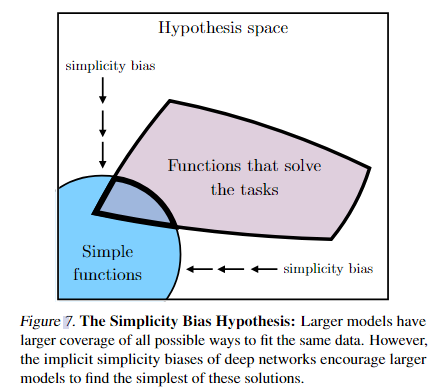
在这里插入图片描述

  • 尽管大模型的容量足够大，可以拟合极为复杂的函数，但深度网络在训练过程中有一种“隐含的偏好”，倾向于找到最简单、最自然的解决方案。具体来说，大模型覆盖更广的假设空间 → 有能力找到所有可能解；但由于优化算法（如梯度下降）和网络结构本身的偏置，模型更容易收敛到简单函数区域（Simple functions）；因此，更大的模型反而可能学到更“干净”、更通用的规律。

4.4 总结

1. 任务广义性 (Task Generality)

  • 当模型必须解决越来越多的任务（比如同时做分类、生成、对比学习），解空间会越来越小。因为满足所有约束的表示只有少数，模型最终都被“推向”相似的表示。例如，一个只学会区分“猫 vs 狗”的模型，可能有多种特征组合；但一个必须处理“猫、狗、马、鸟、鱼”等任务的模型，就只能学习到更普适、更抽象的表示（比如“腿的数量”“是否有翅膀”），不同模型最终会学到相似的结构。

2. 模型容量 (Model Capacity)

  • 大模型更容易收敛到相同的解。因为它们搜索函数空间的能力更强，遇到的任务目标相同，最终找到的“最优表示”趋于一致。例如，两个大语言模型，架构不同（GPT vs LLaMA），但在足够大数据和相同任务目标下，它们的中间表示会逐渐对齐（比如“苹果”与“fruit”的语义嵌入接近）。

3. 简约偏置 (Simplicity Bias)

  • 深度网络偏好简单的解，这让它们不会发散到千奇百怪的复杂表示，而是自然收敛到小范围内的“简单表示”。例如，不同卷积网络在早期层都会学到类似的“边缘检测”滤波器，这是最简单又最通用的图像特征，结果大家都收敛到了这个解。

4、表示之所以趋同，是因为：

  • 任务约束让解空间越来越小（越通用，越收敛）；

  • 模型容量让大模型更容易找到共同最优解；

  • 简约偏置让深度网络天然选择相似的简单解。

  • 三者结合，使得不同架构、不同目标的模型，最终仍会收敛到相似的表示空间。

五、我们正在收敛到什么样的表示？

认为深度学习模型在大规模任务与数据下训练的结果，不是“拟合数据”，而是在逼近生成世界的统计分布。换句话说：模型最终学习的“表示”，是对现实世界统计规律的一种抽象近似。

5.1 理想化的世界

  • 考虑一个理想化世界。这个世界由一系列离散事件Z=[z1,...,zT]Z = [z_1, ..., z_T]Z=[z1​,...,zT​]组成，这些事件来自某个未知分布P(Z)\mathbb{P}(Z)P(Z)。每个事件都可以通过一个确定性函数被“观测”为某种形式的信号（例如声音、图像、文本、质量、力矩等）。每个观测都是事件到观测空间的一一映射（bijection）。例如，一个事件可以看作“世界在某一时刻的状态”。在理想化条件下，知道了P(Z)\mathbb{P}(Z)P(Z)，就能预测所有观测事件。

  • 这相当于在数学上定义“真实世界”：

    • 世界由真实事件 ZZZ 构成；
    • 能看到的只是它们的投影或观测 X=obs(Z)X = \text{obs}(Z)X=obs(Z)；
    • 模型通过学习 XXX的分布，间接地学习到了ZZZ 的分布。

  • 这是一种理想化假设，真实世界会有噪声与不完备，但它帮助我们推导理论收敛。

5.2 一类对比学习模型收敛到$\mathbb{P}(Z) $的表示

  • 考虑一类“对比学习者”，它们通过建模“共同出现的观测”来学习表示。对于两个观测 xa,xbx_a, x_bxa​,xb​，我们定义它们在时间窗口 $T_\text{window} $ 内同时出现的共现概率：

​ Pcoor(xa,xb)∝∑(l,l′):∣l−l′∣≤TwindowP(Xl=xa,Xl′=xb)P_{\text{coor}}(x_a, x_b) \propto \sum_{(l,l'): |l - l'| \leq T_{\text{window}}} P(X_l = x_a, X_{l'} = x_b)Pcoor​(xa​,xb​)∝(l,l′):∣l−l′∣≤Twindow​∑​P(Xl​=xa​,Xl′​=xb​)

  • 接着，定义“正样本”（positive pairs）为时间上相近的观测，而“负样本”（negative pairs）为随机采样的观测。模型的任务是学习一个表示函数 $f_X $，使得：

​ $\langle f_X(x_a), f_X(x_b) \rangle \approx \log \frac{P_\text{pos}(x_a, x_b)}{P_\text{neg}(x_a, x_b)} $

  • 即点积近似“正负对数几率”（log odds）。

  • 这与常见的对比学习目标（如 InfoNCE、SimCLR、SimCSE）是一致的。在温和条件下，最优的表示 $f_X $收敛到：

​ $\langle f_X(x_a), f_X(x_b) \rangle = K_{\text{PMI}}(x_a, x_b) + c_X $

  • 其中 $K_{\text{PMI}} $ 是点互信息核（pointwise mutual information kernel）。

具体来说：

  • 对比学习本质上是在学习点互信息（PMI）结构；
  • PMI 反映了样本间的统计共现关系；
  • 这意味着模型学到的表示与数据背后的统计分布 $\mathbb{P}(Z) $ 有关。

因此，在足够的训练下，这些模型会收敛到表示 $\mathbb{P}(Z) $ 的结构。

  • 推广到多模态情况：不同模态（如图像、语音、文本）若都来自相同的底层事件 $Z $，则它们的 PMI 结构一致：

​ $K_{\text{PMI}}(z_a, z_b) = \langle f_X(x_a), f_X(x_b) \rangle = \langle f_Y(y_a), f_Y(y_b) \rangle $

  • 这意味着不同模态的模型会收敛到同一个统计核心表示。

  • 这说明为什么多模态表示（如 CLIP）能对齐视觉与语言空间：它们都在逼近同一个底层世界分布 $\mathbb{P}(Z) $。

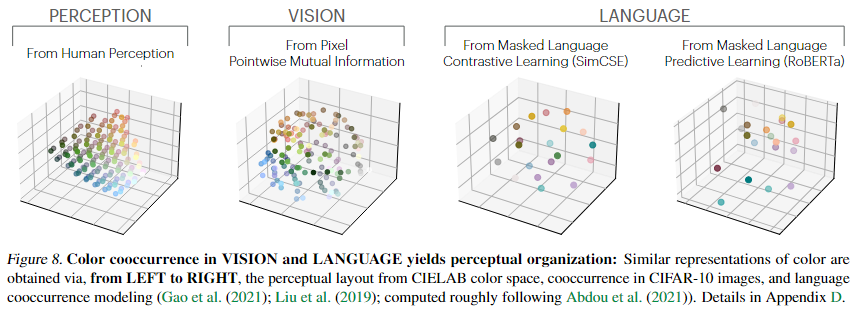
在这里插入图片描述

  • 上图表示视觉模型与语言模型学习到的颜色表示空间，与人类感知空间高度一致。
  • 模型（无论是视觉的还是语言的）**通过共现学习（cooccurrence learning）**就能自发地获得对现实世界的结构性理解；
  • 表示学习的结果并不依赖任务本身，而是由底层数据统计规律 P(Z)\mathbb{P}(Z)P(Z) 决定；
  • 语言与视觉模型可能在内部共享相同的“世界表示结构”。
  • 视觉与语言模型的颜色空间都与人类感知高度一致。
  • 模型的表示本质上反映了底层世界的统计规律，而非单纯任务特征。

六、收敛的意义是什么

6.1 扩大规模（Scaling）足够导致收敛，但不一定高效

  • 当参数量、数据量、计算量不断扩增时，表示将趋于收敛，不论模型结构或模态差异。
  • 虽然“变大”最终会学到相似的表示，但不同算法到达同样的效果所需资源差异很大。要想真正有效地收敛到世界的统计模型，还必须满足一些理论条件。
  • 这解释了为什么有的模型小但聪明（结构优），有的模型大却不灵（学习不稳定）。

6.2 训练数据可以跨模态共享

  • 如果存在一个模态无关的柏拉图式表示（Platonic representation），那么图像与语言数据都能帮助模型学习到相同的底层结构。
  • 这就是为什么 CLIP、GPT-4V 这类模型能共享语言与图像知识：它们都在学习同一个底层世界的统计结构。甚至作者提出了一个换算率：1个词相当于b个像素，说明语言与视觉数据在信息量上可互换。
  • 要训练最好的视觉模型，不仅应使用图像数据 $N $，也应使用文本数据 $M $。

6.3 条件生成比无条件生成更容易

  • 当我们以已知数据为条件时，条件数据可能与底层柏拉图结构更接近，因此模型学习得更快、更稳定。

6.4 收敛的表示可以作为模态之间的桥梁

  • 这种桥梁使得我们无需成对数据也能实现模态映射，语言模型能理解视觉数据，是因为它们共享相同的底层表示结构。

6.5 扩大模型规模可能减少幻觉与偏差

  • LLMs 目前的主要缺陷之一是“幻觉”（hallucination）——生成错误事实。如果模型规模继续扩展，逼近真实世界统计规律（P(Z)\mathbb{P}(Z)P(Z)），那么幻觉可能会随之减少。但前提是：数据足够多样且无损，否则模型只是更准确地反映偏差，而不是消除偏差。
  • 大模型不会“放大”偏差，而是忠实复制数据的统计倾向

七、反例与局限

7.1 不同模态可能包含不同信息

  • 本文在此承认其假设前提：模型必须学习相同的信息投影（bijection）。若模态之间存在信息损失（lossy）或随机噪声，就无法保证完全收敛。

  • 例如：

    • 语言可以描述“我相信言论自由”；
    • 图像却无法表达这个抽象概念；
    • 反之，图像能表现日全食的视觉体验，而语言难以传达。

    因此，两种模态不可能完全收敛到同一表示，除非它们拥有相同的信息内容。

7.2 当信息量与容量足够时，模型会收敛

  • 本文的假设只在模型容量足够大、输入信息足够高时成立。当输入信号信息丰富、模型容量足够时，不同模态的模型可收敛到相同的表示；否则，它们只能收敛到部分重叠的低维结构。
  • 这解释了为什么小模型或单模态模型收敛效果差； 以及为何高容量多模态模型（如 GPT-4）表现出“世界知识一致性”。

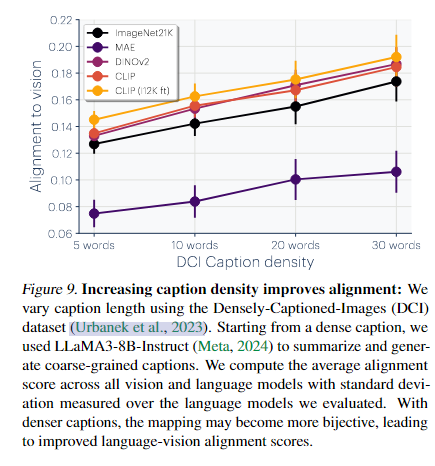
在这里插入图片描述

  • 上图表示跨模态表示的对齐（alignment）依赖于输入信息的丰富度与映射的可逆性（bijectivity）

7.3 目前并非所有模态的表示都在收敛

  • 在机器人技术中，还没有一种标准化的方法来表示世界状态，就像用于表示图像和文本一样。一个限制在于机器人中使用的硬件，这通常是昂贵和缓慢的。这在训练数据的数量和多样性方面造成了瓶颈。

7.4 产生AI模型的社会学偏见

  • AI 社群本身的文化偏好也影响了收敛方向。
  • 这是一种“社会学偏差”：AI 的收敛不完全是自然规律，也受到人类设计取向的影响。

7.5 专用智能可能不会收敛

  • 如果系统只为特定任务（如蛋白质折叠或自动驾驶）设计，那么它的表示可能完全脱离“真实世界结构”。
  • 本文的收敛假设仅适用于通用智能（general intelligence）； 专用系统会学习到局部的、任务依赖的表示，而非世界级结构。

7.6 我们如何测量“表示对齐”？

  • 论文中使用的是互为最近邻（mutual nearest-neighbor）指标，但作者承认这并非完美； 不同度量可能给出不同结果
    面造成了瓶颈。

7.4 产生AI模型的社会学偏见

  • AI 社群本身的文化偏好也影响了收敛方向。
  • 这是一种“社会学偏差”：AI 的收敛不完全是自然规律，也受到人类设计取向的影响。

7.5 专用智能可能不会收敛

  • 如果系统只为特定任务（如蛋白质折叠或自动驾驶）设计，那么它的表示可能完全脱离“真实世界结构”。
  • 本文的收敛假设仅适用于通用智能（general intelligence）； 专用系统会学习到局部的、任务依赖的表示，而非世界级结构。

7.6 我们如何测量“表示对齐”？

  • 论文中使用的是互为最近邻（mutual nearest-neighbor）指标，但作者承认这并非完美； 不同度量可能给出不同结果
# 人工智能
Logo
北京朝阳AI社区

更多推荐

从[Java · 初窥门径] 运算符 — 位运算符v

与传统程序不同，智能体不仅仅是被动执行预设指令，而是具备一定程度的自主性和适应性，能够在复杂、多变的环境中不断优化行为。无论是任务分解、知识获取，还是与外部工具的协同，都会结合实际案例，帮助你理解如何打造一个真正能落地、能进化的智能体。它模拟了人类作者“写—审—改”的迭代过程：一个模型负责生成候选答案，另一个模型则充当评估员，给出改进建议，二者循环迭代，直到得到令人满意的结果。简而言之，评估器–优

avatar 北京朝阳AI社区

智能化软件开发：传统程序员的转型之路

在当今科技飞速发展的时代，智能化已经成为软件开发领域的重要趋势。传统的软件开发模式在面对日益复杂的业务需求和海量的数据处理时，逐渐暴露出效率低下、灵活性不足等问题。本文章的目的在于帮助传统程序员了解智能化软件开发的核心概念、技术和方法，引导他们顺利实现向智能化软件开发领域的转型。文章将涵盖智能化软件开发的各个方面，包括核心概念、算法原理、数学模型、项目实战、应用场景以及相关的工具和资源等。核心概念

avatar 北京朝阳AI社区

疑大模型之Spring AI实战系列（十一）：Spring Boot + OpenAI 集成本地向量数据库Chromaa

缓存的本质是利用时间局部性（Temporal Locality）和空间局部性（Spatial Locality）原理，将频繁访问的数据存储在更快的存储介质中。本文将深入探讨C#环境下多级缓存的架构设计与实现，重点分析内存缓存（Memory Cache）与Redis分布式缓存的协同工作机制，并详细阐述如何通过Redis的发布-订阅（Pub/Sub）模式实现不同节点间的缓存状态同步。// 简化的大小计

avatar 北京朝阳AI社区