一文通透NSA——动态分层下的“原生稀疏注意力”策略：将粗粒度的token压缩与细粒度的token选择相结合(含DSA的详解)

v_JULY_v

1087人浏览 · 2025-10-03 20:43:44

v_JULY_v · 2025-10-03 20:43:44 发布

前言

今25年年初，deepseek R1(包括V3)席卷全球，引发所有大模型同仁的高度关注，我当时在博客内也解读了很多相关的论文

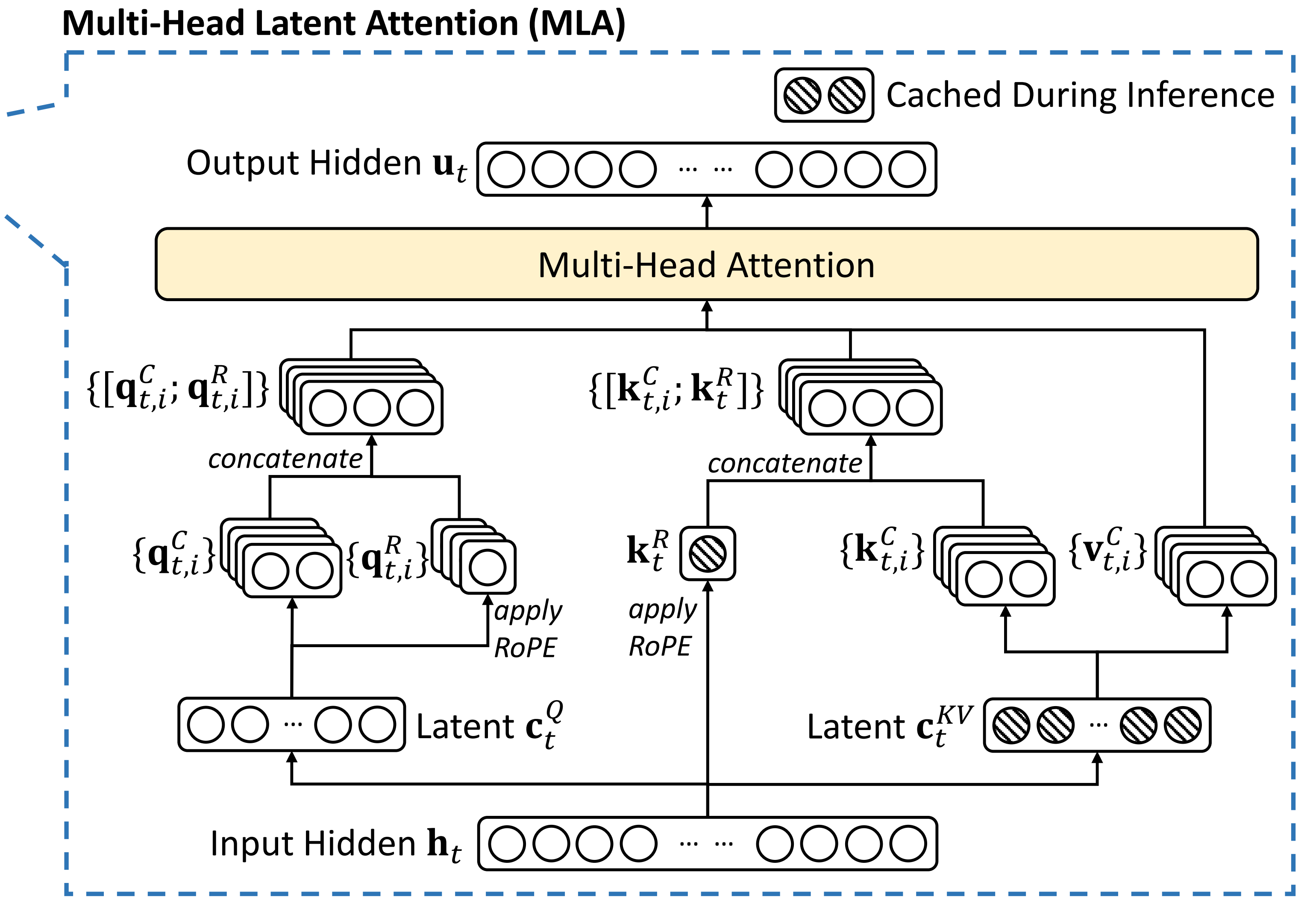
比如下图解读过的MLA『当然值得提前强调的是，其实MLA本质上是属于做MHA之前的前置工作(减少KV-Cache，而非减少注意力的计算)，属于对MHA的前置改进，而本文要介绍的NSA便是对注意力机制对直接的改进』

更多详见《火爆全球的DeepSeek系列模型》

再后来的25年2月，来自DeepSeek、北大和华盛顿大学的研究人员提出了一种全新的注意力机制NSA，NSA是DeepSeek-R1「爆火出圈」后的第一篇论文

然，为了解读这个NSA，也是经历了一番曲折的，具体如下

25年4.23，我司LLM论文100课程中的一学员朋友Michael当时建议说，希望讲下deepseek最新的论文
1 NSA稀疏注意力
Hardware-Aligned and Natively Trainable Sparse Attention
2 SPCT强化学习
Inference-Time Scaling for Generalist Reward Modeling
但4月下旬那会，大部分精力都在研究VLA π0及其后续的改进π0.5上，使得当时实在是没有时间、心思、精力来解读NSA

哪怕虽然其于25年5月份被ACL 2025录用，更于25年7月斩获ACL 2025最佳论文
可5-7月份的这段时间，正是我司长沙具身团队第一轮突飞猛进之时，更没时间去解读这个NSA了
然，25年9月底(国庆假期之前)，DeepSeek最新模型V3.2-Exp发布，推出全新注意力机制DeepSeek Sparse Attention(DSA)，而这个DSA便是对NSA的改进
十一假期之前，我司长沙具身团队完成了一系列工作，而如今十一假期来临，整整有8天的时间，故可以抽时间解读下这个NSA和DSA了

最后，顺带说两点

本文基于的NSA和DSA两篇原论文，和相关文章(比如微信好友小冬瓜AIGC的手撕NSA)写就
其中的核心内容基于原论文而解读，但远非单纯的翻译——如果你看的仔细的话即非走马观花
当然了，如果只是单纯的翻译，大家随手都能找个翻译工具翻译，本文章也不会有如此广大的受众、及如此强大的影响力了
虽说现在侧重具身了，但大模型与具身智能是密不可分的，要不然就不会出来很多所谓的具身大模型了，故大模型会是我个人的第二研究方向，也是本博客内会持续解读、分享的第二方向

第一部分 Native Sparse Attention：硬件对齐且原生可训练的稀疏注意力

1.1 引言与相关工作

1.1.1 引言

如原NSA论文所说，25年年初那会，国内外陆续推出的OpenAI 的 o-series 模型、DeepSeek-R1（DeepSeek-AI，2025）和 Gemini 1.5 Pro（Google 等，2024），使得模型能够处理整个代码库、长文档，维持数千 token 的连贯多轮对话，并在长距离依赖下进行复杂推理

然而，原始 Attention 机制的高复杂度已成为一个关键难题，且随着序列长度的增加，延迟瓶颈愈发明显。理论估算表明，在解码64k长度上下文时，基于softmax架构的注意力计算占总延迟的70–80%，这凸显了开发更高效注意力机制的迫切需求
一种高效长上下文建模的自然方法是利用softmax注意力机制中固有的稀疏性
Ge等，2023；即Model Tells You What to Discard: Adaptive KV Cache Compression for LLMs
Jiang等，2023即LLMLingua: Compressing Prompts for Accelerated Inference of Large Language Models
即通过有选择地计算关键的query-key对，可以在保持性能的同时显著降低计算开销

近期的研究进展通过多种策略展示了这种潜力：包括
KV-cache逐出方法
$\rightarrow$ Li等，2024，即SnapKV: LLM Knows What You are Looking for Before Generation
$\rightarrow$ Zhang等，2023b，即H2O: Heavy-Hitter Oracle for Efficient Generative Inference of Large Language Models，其利用“重击者”token（高频访问的key-value对）进行KV缓存管理，在推理阶段动态维护最重要的token，减少内存和计算开销
$\rightarrow$ Zhou等，2024，即BUZZ: Beehive-Structured Sparse KV Cache with Segmented Heavy Hitters for Efficient LLM Inference

分块KV-cache选择方法
Gao等，2024，即SeerAttention: Learning Intrinsic Sparse Attention in Your LLMs
Tang等，2024，即Quest: Query-aware Sparsity for Efficient Long-context LLM Inference，其基于查询感知的稀疏注意力机制，动态选择重要的key-value块，减少计算量，适用于长上下文推理
Xiao等，2024a，即InfLLM: Training-free Long-context Extrapolation for LLMs with an Efficient Context Memory

以及基于采样、聚类或哈希的选择方法
Chen等，2024b，即MagicPIG: LSH Sampling for Efficient LLM Generation，其利用局部敏感哈希（LSH）进行token采样，减少注意力计算量，提升大模型生成效率
Desai等，2024，即HashAttention: Semantic Sparsity for Faster Inference
Liu等，2024，即ClusterKV: Manipulating LLM KV Cache in Semantic Space for Recallable Compression，其在语义空间中对KV缓存进行聚类压缩，提升缓存的可召回性和压缩效率，适用于长文本建模

尽管这些策略前景可观，但现有的稀疏注意力方法在实际部署中往往表现不佳。许多方法未能实现与理论加速相匹配的速度提升
此外，大多数方法在训练阶段缺乏有效的支持，难以充分利用注意力的稀疏模式

为了解决这些局限性，高效稀疏注意力的部署必须应对两个关键挑战：

硬件对齐的推理加速：要将理论上的计算量减少转化为实际的速度提升，需要在预填充和解码阶段设计符合硬件友好的算法，以缓解内存访问和硬件调度瓶颈
训练感知的算法设计：通过可训练算子实现端到端计算，以降低训练成本，同时保持模型性能。这些要求对于实现快速长上下文推理或训练的实际应用至关重要

然而，综合考虑以上这两个方面，现有方法仍然存在明显差距

为了实现更高效且有效的稀疏注意力机制，来自的研究者提出了NSA，这是一种原生可训练的稀疏注意力架构，融合了层次化的token建模

如图2所示

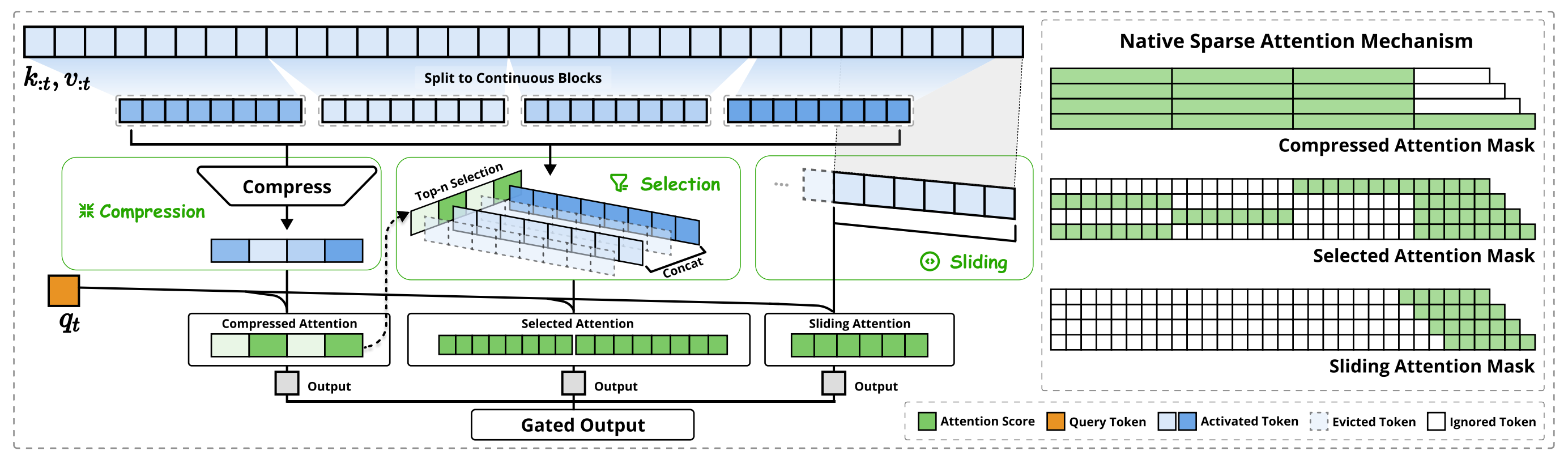
NSA通过将keys和values组织为时间块，并通过三条注意力路径进行处理，从而降低每个查询的计算量：

分别为压缩的粗粒度token
有选择性保留的细粒度token
以及用于本地上下文信息的滑动窗口

然后作者还实现了专用内核，以最大化其实用效率

总之，NSA 引入了两项核心创新

硬件对齐系统：优化块状稀疏注意力，以充分利用张量核心和内存访问，确保算术强度的平衡
训练感知设计：通过高效的算法和反向算子，实现端到端训练的稳定性
这一优化使 NSA 同时支持高效部署和端到端训练

1.1.2 相关工作：重新思考稀疏注意力方法

现代稀疏注意力方法在降低 Transformer 模型理论计算复杂度方面取得了显著进展。然而，大多数方法主要在推理阶段应用稀疏性，同时保留了预训练的全注意力骨干网络，这可能引入架构偏差，从而限制其充分发挥稀疏注意力优势的能力

此话怎讲呢，请看下文

首先，是高效推理的错觉

尽管在注意力计算中实现了稀疏性，许多方法仍未能相应降低推理延迟，主要原因有两个：

阶段受限的稀疏性。诸如 H2O（Zhang 等，2023b）的方法在自回归解码过程中应用稀疏性，但在预填充阶段则需要计算量巨大的预处理（例如注意力图计算、索引构建）
相比之下，MInference（Jiang 等，2024）等方法仅关注预填充阶段的稀疏性

这些方法无法在所有推理阶段实现加速，因为至少有一个阶段的计算成本与全注意力机制相当
阶段专用性降低了这些方法在以预填充为主的任务（如图书摘要和代码补全）或以解码为主的任务（如长链式思维推理（Wei 等，2022））中的加速能力
与先进注意力架构的不兼容性
一些稀疏注意力方法无法适应现代高效解码架构，例如多查询注意力（MQA）（Shazeer, 2019）和分组查询注意力（GQA）（Ainslie 等,2023）
这些架构通过在多个查询头之间共享KV『详情参见此文《一文通透各种注意力：从多头注意力MHA到分组查询注意力GQA、多查询注意力MQA》』，有效减少了解码过程中的内存访问瓶颈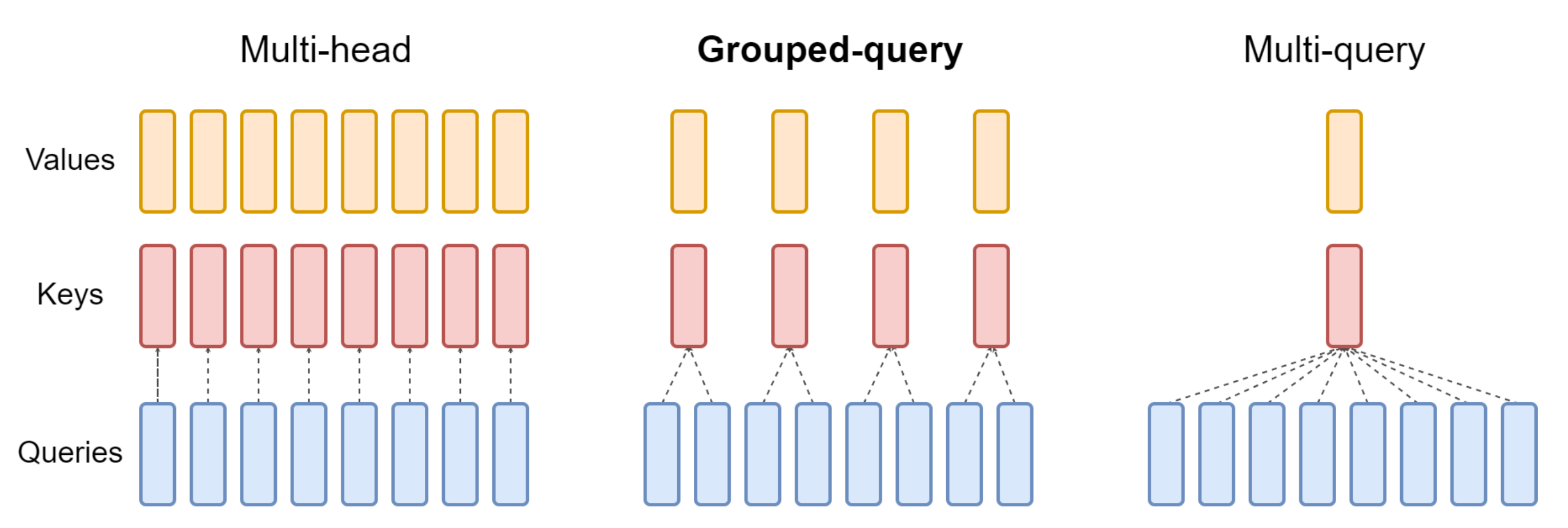

例如，在 Quest（Tang 等, 2024）等方法中，每个注意力头会独立选择其KV缓存子集
$\rightarrow$ 虽然该方法在多头注意力（MHA）模型中表现出一致的计算稀疏性和内存访问稀疏性
$\rightarrow$ 但在基于GQA等架构的模型中，情况则有所不同。在GQA此类架构下，KV缓存的内存访问量等于同一GQA分组内所有查询头选择的集合。这一架构特性意味着，尽管这些方法可以减少计算操作，但所需的KV缓存内存访问量仍然较高

这一限制导致了一个关键抉择：尽管部分稀疏注意力方法能减少计算量，但其分散的内存访问模式却与先进架构高效内存访问的设计理念相冲突

这些局限性产生的原因在于，许多现有的稀疏注意力方法主要关注于KV缓存的减少或理论计算量的降低，但在先进的框架或后端中却难以实现显著的延迟降低

因此，这促使作者开发结合先进架构设计与硬件高效实现的算法，以充分利用稀疏性，从而提升模型效率

其次，作者在重新审视可训练稀疏性的神话时，发现

性能退化：事后应用稀疏性会迫使模型偏离其预训练时的优化轨迹。如Chen等人（2024b）所示，前20%的注意力仅能覆盖70%的总注意力分数「As demonstrated by Chen et al.(2024b), top 20% attention can only cover 70% of the total attention scores」
这使得预训练模型中的检索头等结构在推理阶段易受剪枝影响
训练效率需求：高效处理长序列训练对于现代大模型（LLM）开发至关重要。这不仅包括在更长文档上的预训练以提升模型容量，还包括后续如长上下文微调和强化学习等适应阶段。

然而，现有稀疏注意力方法主要针对推理场景，训练过程中的计算挑战基本未被解决。这一局限阻碍了通过高效训练开发更强大长上下文模型的进程

此外，将现有稀疏注意力方法适配到训练过程中也暴露出诸多挑战

不可训练组件
ClusterKV（Liu 等，2024）（包括 k-means 聚类）和MagicPIG（Chen 等，2024b）（包括基于 SimHash 的选择）等方法中的离散操作，会在计算图中产生不连续性
这些不可训练的组件阻碍了梯度在token选择过程中的传播，从而限制了模型学习最优稀疏模式的能力
低效的反向传播
一些理论上可训练的稀疏注意力方法存在实际训练低效的问题
像 HashAttention（Desai 等，2024）这类方法采用的基于token 粒度的选择策略，在注意力计算过程中需要从 KV 缓存中加载大量单独的token
这种非连续的内存访问方式阻碍了如 Flash Attention 等快速注意力技术的高效适配，而Flash Attention这些技术依赖于连续的内存访问和分块计算以实现高吞吐量
因此，实际实现不得不退回到较低的硬件利用率，导致训练效率显著下降

总之，如小冬瓜AIGC所说

对于注意力设计，有Flash Attention这样优秀的工作，但是并未通过减少注意力计算量而进行加速。假设上下文是无限长，可以如下处理，控制上下文序列的长度：

RNN/线性Attention：将过去的状态压成隐状态

窗口注意力：限制注意力计算的可视范围

稀疏化：按照一定的识别只筛选有限的token做注意力计算

1.2 NSA的整体方法论

1.2.0 对注意力机制的回顾与NSA的整体简介

首先，对于注意力机制而言

根据此文《Transformer通俗笔记：从Word2Vec、Seq2Seq逐步理解到GPT、BERT》可知，在注意力机制中，每个查询token $\mathbf{q}_{t}$ 会针对所有前面的键 $\mathbf{k}_{: t}$ 计算相关性分数，以生成值 $\mathbf{V}_{: t}$ 的加权和。具体来说，对于长度为 $t$ 的输入序列，注意力操作被定义为下面所述的公式1：

$\mathbf{o}_{t}=\operatorname{Attn}\left(\mathbf{q}_{t}, \mathbf{k}_{: t}, \mathbf{v}_{: t}\right)$

其中 Attn 表示注意力函数：

$\operatorname{Attn}\left(\mathbf{q}_{t}, \mathbf{k}_{: t}, \mathbf{v}_{: t}\right)=\sum_{i=1}^{t} \frac{\alpha_{t, i} \mathbf{v}_{i}}{\sum_{j=1}^{t} \alpha_{t, j}}, \quad \alpha_{t, i}=e^{\frac{\mathbf{q}_{t}^{\top} \mathbf{k}_{i}}{\sqrt{d_{k}}}}$

其中， $\alpha_{t, i}$ 表示 $\mathbf{q}_{t}$ 与 $\mathbf{k}_{i}$ 之间的注意力权重， $d_{k}$ 是键的特征维度。随着序列长度的增加，注意力计算在整体计算成本中所占比重不断上升，这对长上下文处理带来了重大挑战

如小冬瓜所说，在上述公式中，我们可以控制 $\mathbf{k}_{: t}$ 和 $\mathbf{v}_{: t}$ 的数量，如 $\mathbf{k}_{t / 2: t}$ 和 , 仍然能够得到同个维度的输出, 但是注意力输出是有区别的，如下所示：

其次，对于算术强度而言

算术强度是计算操作次数与内存访问次数的比值，它本质上决定了算法在硬件上的优化方式。每个GPU都有一个由其峰值计算能力和内存带宽决定的临界算术强度，这一临界值通过这两项硬件参数的比值计算得出

对于计算任务来说
$\rightarrow$ 当算术强度高于这一临界值时，任务受限于GPU的浮点运算能力（FLOPS），即为计算受限
$\rightarrow$ 而当算术强度低于临界值时，任务则受限于内存带宽，即为内存受限
具体而言，对于因果自注意力机制
在训练和预填充阶段，批量矩阵乘法和注意力计算表现出较高的算术强度，使这些阶段在现代加速器上受到计算能力的限制
相比之下，自回归解码由于每次前向传播仅生成一个token，同时需要加载整个键值缓存，因此受限于内存带宽，导致算术强度较低

从而导致了不同的优化目标——在训练和预填充阶段降低计算成本，而在解码阶段则减少内存访问

最后，对于NSA的整体框架而言

为了充分利用具有自然稀疏模式的注意力机制的潜力，作者提出将公式1 $\mathbf{o}_{t}=\operatorname{Attn}\left(\mathbf{q}_{t}, \mathbf{k}_{: t}, \mathbf{v}_{: t}\right)$ 中的原始键值对 $\mathbf{k}_{: t}, \mathbf{v}_{: t}$ 替换为每个查询 $\mathbf{q}_{t}$ 所对应的更紧凑且信息密集的表示键值对 $\tilde{K}_{t}, \tilde{V}_{t}$

具体而言，作者正式定义优化后的注意力输出如下：

$\begin{array}{c} \tilde{K}_{t}=f_{K}\left(\mathbf{q}_{t}, \mathbf{k}_{: t}, \mathbf{v}_{: t}\right), \quad \tilde{V}_{t}=f_{V}\left(\mathbf{q}_{t}, \mathbf{k}_{: t}, \mathbf{v}_{: t}\right) \\ \mathbf{o}_{t}^{*}=\operatorname{Attn}\left(\mathbf{q}_{t}, \tilde{K}_{t}, \tilde{V}_{t}\right) \end{array}$

其中 $\tilde{K}_{t}, \tilde{V}_{t}$ 是根据当前查询 $\mathbf{q}_{t}$ 和上下文记忆 $\mathbf{k}_{: t}, \mathbf{v}_{: t}$ 动态构建的。可以设计多种映射策略，以获得不同类别的 $\tilde{K}_{t}^{c}, \tilde{V}_{t}^{c}$ ，并将它们组合如下——定义为公式5：

$\mathbf{o}_{t}^{*}=\sum_{c \in C} g_{t}^{c} \cdot \operatorname{Attn}\left(\mathbf{q}_{t}, \tilde{K}_{t}^{c}, \tilde{V}_{t}^{c}\right)$

如图2所示

NSA有三种映射策略 $C=\{\mathrm{cmp}, \mathrm{slc}, \mathrm{win}\}$ ，分别代表对键和值的压缩、选择、滑动窗口
『NSA have three mapping strategies C = {cmp, slc, win}, representing compression, selection, and sliding window for keys and values』
$g_{t}^{c} \in[0,1]$ 是门控分数，用于对应策略 $c$ ，由输入特征通过MLP和sigmoid激活函数获得

令 $N_{t}$ 表示重映射键/值的总数

$N_{t}=\sum_{c \in C} \operatorname{size}\left[\tilde{K}_{t}^{c}\right]$

作者通过确保 $N_{t} \ll t$ 来维持较高的稀疏率

如小冬瓜所说(当然在下文中，我新增了一些补充说明)，NSA在KV序列的不同尺度上取舍，即是上述所说先筛选合适的KV再算注意力

压缩注意力：把控全局信息

选择注意力：把控局部信息

滑窗注意力：把控关联紧密信息

脱离原论文公式，在NSA的框架图里用最简单的数值来描述，计算注意力前有 $\mathbf{q}_{: t}$ 和 $\mathbf{k}_{: t}$ 、 $\mathbf{v}_{: t}$

词元序列 $t$ 为32，即左上顶部蓝色方格长条每一格代表第 $i$ 时刻的 $\mathbf{k}_{i}$ 、 $\mathbf{v}_{i}$

将整个长序列 $\mathbf{k}_{: 32}$ 、 $\mathbf{v}_{: 32}$ 按照长度为 8 划分为4块
$\mathbf{k}_{1: 8}^{(1)}, \mathbf{v}_{1: 8}^{(1)}$ 、 $\mathbf{k}_{8: 16}^{(2)}, \mathbf{v}_{8: 16}^{(2)}$ 、 $\mathbf{k}_{16: 24}^{(3)}, \mathbf{v}_{16: 24}^{(3)}$ 、 $\mathbf{k}_{24: 32}^{(4)}, \mathbf{v}_{24: 32}^{(4)}$ ....

压缩：将每个KV块压成一个向量即 $\mathbf{k}_{1: 8}^{(1)} \rightarrow \tilde{\mathbf{k}}^{(1) \mathrm{cmp}} \in \mathcal{R}^{d \times c}$ , 同理，压缩的目的是把一段长度为8的序列压成 $c$ 个序列, 并且有关系 $c<8$
为了便于理解可将 $c = 1$ 既是1个token代表了一序列——从而4个token代表了4个原本长度为8的序列不就意味着4个新token代表了原来32个老token了么
至于怎么压缩我们后面探讨。这里的压缩注意力是 $\mathbf{q}_{32}$ 和4个段落的 $\tilde{\mathbf{k}}^{(\mathrm{b}) \mathrm{cmp}}, b=1,2,3,4$ 进行计算得到4个注意力分数，所以将v进行计算后，就得到压缩的注意力输出了，代表了全局信息 $o_{32}^{(\mathrm{cmp})} \in \mathcal{R}^{d \times 1}$

选择：在压缩时得到的段落注意力分数，选择top-2, 即第2和第4的绿色块。那么就能找到对应的段落块当成局部信息 $\mathbf{k}_{8: 16}^{(2)}, \mathbf{v}_{8: 16}^{(2)}$ 、 $\mathbf{k}_{24: 32}^{(4)}, \mathbf{v}_{24: 32}^{(4)}$ ，获取到KV后也可以计算选择注意力，最终为 $o_{32}^{(\text {sle })} \in \mathcal{R}^{d \times 1}$

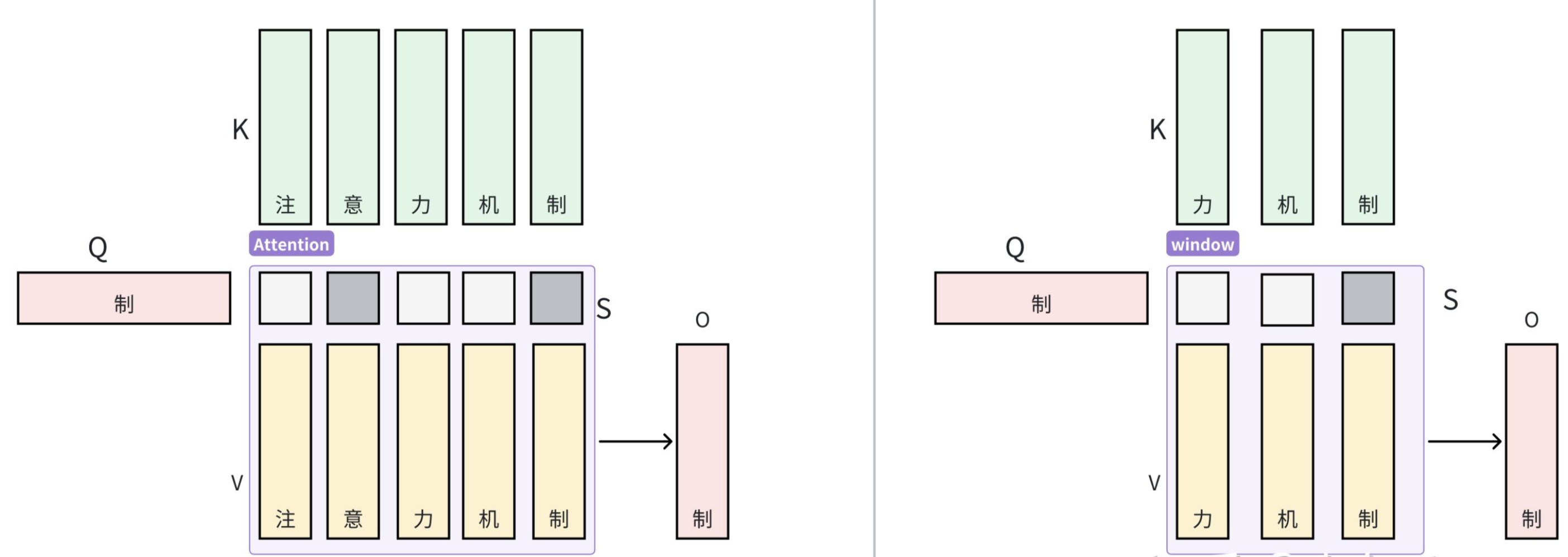
滑窗：在原 $\mathbf{k}_{: 32}, \mathbf{v}_{: 32}$ 序列里取就近的8 个键和值 $\mathbf{k}_{24: 32}, \mathbf{v}_{24: 32}$ ，同样可以得到滑窗注意力为 $o_{32}^{(\mathrm{win})} \in \mathcal{R}^{d \times 1}$

门控：汇聚三种注意力 $g_{32}^{(c m p)} o_{32}^{(\mathrm{cmp})}+g^{(s l e)} o_{32}^{(\mathrm{sle})}+g^{(w i n)} o_{32}^{(\mathrm{win})}$ , 其中门控 $g$ 为输入 $x_{32}$ 进行线性层变换并加入sigmoid激活得到。门控是可学习的

至此可以再进一步分析

原来有 $t = 32$ 个上下文KV，在压缩/选择/滑窗里分别有 $N_{t}=4+8 * 2+8=28$ 个上下文KV，实现了注意力的减少

当上下文为64k时, 如果我们取128个全局压缩KV，8个512选择块KV和就近窗口4096个KV, 那么得到了压缩倍数7.88：

$65536 /(128+8 \times 512+4096)=65536 / 8320 \approx 7.88$

1.2.1 token压缩

通过将连续的键或值块聚合为块级表示，可以获得能够捕捉整个块信息的压缩键和值

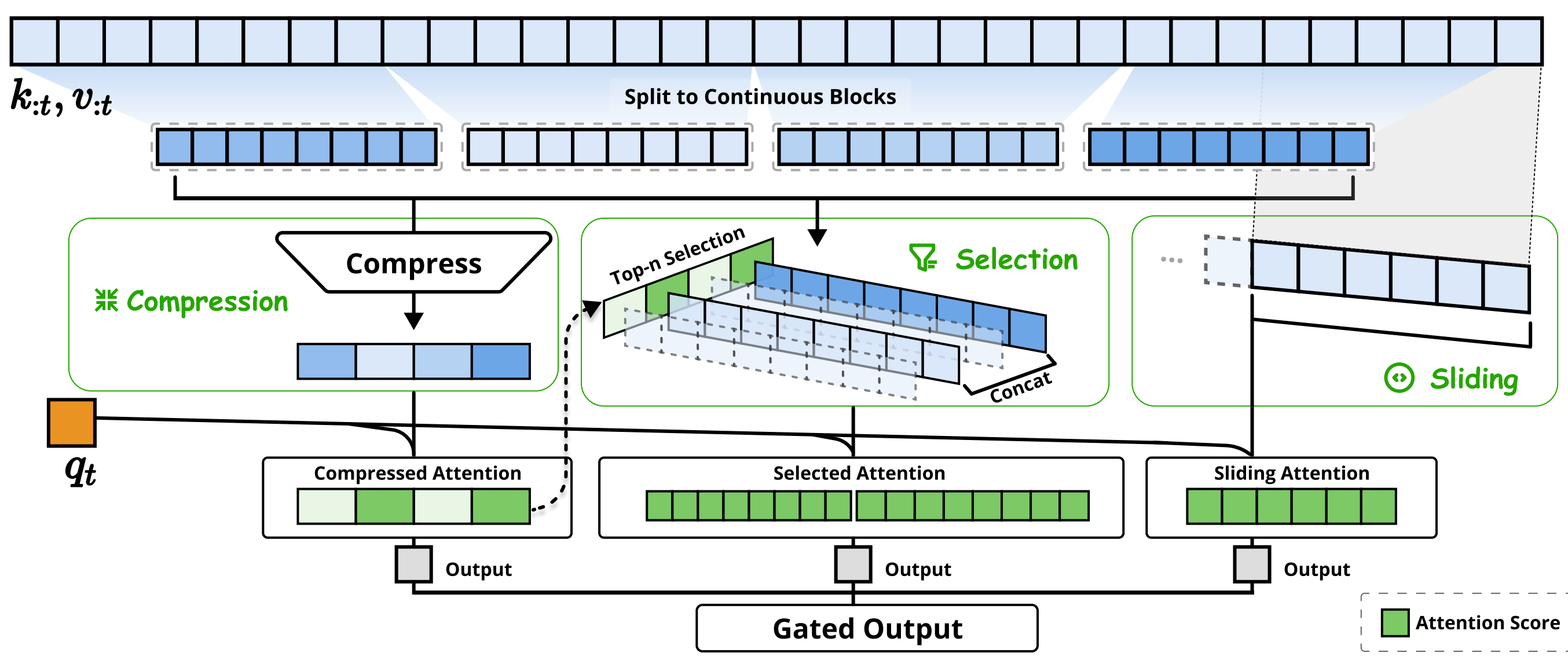
形式上，压缩键的表示定义如下：

$\tilde{K}_{t}^{\mathrm{cmp}}=f_{K}^{\mathrm{cmp}}\left(\mathbf{k}_{: t}\right)=\left\{\varphi\left(\mathbf{k}_{i d+1: i d+l}\right) \left\lvert\, 0 \leqslant i \leqslant\left\lfloor\frac{t-l}{d}\right\rfloor\right.\right\}$

其中

$l$ 是块长度， $d$ 是相邻块之间的滑动步幅， $\varphi$ 是带有块内位置编码的可学习MLP，用于将块内的key 映射为一个压缩key
$\tilde{K}_{t}^{\mathrm{cmp}} \in \mathbb{R}^{d_{k} \times\left\lfloor\frac{t-l}{d}\right\rfloor}$ 是由压缩key 组成的张量
通常，采用d < l 来缓解信息碎片化
对于压缩的value 表示 $\tilde{V}_{t}^{\mathrm{cmp}}$ 也有类似的公式

压缩表示能够捕捉更粗粒度的高层语义信息，并减少注意力的计算负担

1.2.2 token选择

仅使用压缩后的键和值可能会丢失重要的细粒度信息，因此作者认为，有必要有选择性地保留部分关键的键和值。下面将介绍一种高效的token选择机制，该机制能够以较低的计算开销识别并保留最相关的token

分块选择
作者的选择策略以空间上连续的块处理键和值序列，这一设计受到两个关键因素的驱动：硬件效率的考量和注意力分数固有的分布模式
分块选择对于在现代GPU上实现高效计算至关重要。这是因为现代GPU架构在处理连续块访问时的吞吐量远高于基于随机索引的读取
此外，分块计算能够实现对张量核心的最优利用。这一架构特性使得分块式的内存访问和计算成为高性能注意力机制实现的基本原则，正如FlashAttention的分块设计所体现

分块选择还遵循了注意力分数的固有分布模式。已有研究(Jiang等，2024)表明，注意力分数通常表现出空间连续性，说明相邻的键往往具有相似的重要性水平
为了实现分块选择，作者首先将 key 和 value 序列划分为若干选择块。为了识别在注意力计算中最重要的块，需要为每个块分配重要性分数

那么，如何计算这些块级重要性分数呢
重要性分数计算
计算块的重要性分数可能会带来显著的开销。幸运的是，压缩token的注意力计算会生成中间注意力分数，从而可以利用这些分数来推导选择块的重要性分数
其公式如下：
$\mathbf{p}_{t}^{\mathrm{cmp}}=\operatorname{Softmax}\left(\mathbf{q}_{t}^{T} \tilde{K}_{t}^{\mathrm{cmp}}\right)$

其中
$\mathbf{p}_{t}^{\mathrm{cmp}} \in \mathbb{R}^{\left\lfloor\frac{t-l}{d}\right\rfloor+1}$ 是 $q_t$ 与压缩键 $\tilde{K}_{t}^{\text {cmp }}$ 之间的注意力得分
设 $l^{\prime}$ 表示选择块大小。当压缩块和选择块采用相同的分块方案，即 $l^{\prime}=l=d$ 时，可以直接通过 $\mathbf{p}_{t}^{\mathrm{slc}}=\mathbf{p}_{t}^{\mathrm{cmp}}$ 得到选择块的重要性得分 $\mathbf{p}_{t}^{\text {slc }}$

对于分块方案不同的情况，作者根据它们的空间关系推导选择块的重要性得分
即给定 𝑙 ⩽ 𝑙′，且 𝑑| 𝑙 和 𝑑| 𝑙′，有：
$\mathbf{p}_{t}^{\mathrm{slc}}[j]=\sum_{m=0}^{\frac{l^{\prime}}{d}-1} \sum_{n=0}^{\frac{l}{d}-1} \mathbf{p}_{t}^{\mathrm{cmp}}\left[\frac{l^{\prime}}{d} j-m-n\right]$
其中 [·] 表示用于访问向量元素的索引操作符

对于采用 GQA 或 MQA 的模型，由于键值缓存会在多个查询头之间共享，因此必须确保这些头之间选择块的一致性，以最小化解码过程中的 KV 缓存加载
一个组内各头共享的重要性分数正式定义为：
$\mathbf{p}_{t}^{\operatorname{slc}^{\prime}}=\sum_{h=1}^{H} \mathbf{p}_{t}^{\mathrm{slc},(h)}$
其中， $(h)$ 上标表示头索引， $H$ 表示每组中的查询头数量
该聚合方式确保同一组内各头之间的块选择保持一致
Top-𝑛块选择
在获得选择块的重要性分数后，作者保留位于按块重要性分数排名前 $n$ 的稀疏块中的token，具体公式如下：
$\begin{aligned} \mathcal{I}_{t} & =\left\{i \mid \operatorname{rank}\left(\mathbf{p}_{t}^{\text {slc }^{\prime}}[i]\right) \leqslant n\right\} \\ \tilde{K}_{t}^{\text {slc }} & =\operatorname{Cat}\left[\left\{\mathbf{k}_{i l^{\prime}+1:(i+1) l^{\prime}} \mid i \in \mathcal{I}_{t}\right\}\right] \end{aligned}$

其中
$\operatorname{rank}(\cdot)$ 表示按分数降序排列的位置， $\text { rank = } 1$ 对应最高分
$I_{t}$ 为所选块的索引集合
Cat表示拼接操作
$\tilde{K}_{t}^{\text {slc }} \in \mathbb{R}^{d_{k} \times n l^{\prime}}$ 是由压缩键组成的张量
类似的公式适用于细粒度的值 $\tilde{V}_{t}^{\text {slc }}$ 。所选的键和值随后参与与 $\mathbf{q}_{t}$ 一起进行注意力计算，如公式5所定义
$\mathbf{o}_{t}^{*}=\sum_{c \in C} g_{t}^{c} \cdot \operatorname{Attn}\left(\mathbf{q}_{t}, \tilde{K}_{t}^{c}, \tilde{V}_{t}^{c}\right)$

// 待更

北京朝阳AI社区

更多推荐

上下文工程驱动智能体向游戏NPC自主叙事

上下文工程驱动智能体向游戏NPC自主叙事-摘要

北京朝阳AI社区

基于Q-learning算法在能源市场中实现效益最大化研究（Matlab代码实现）

随着全球能源结构转型和智能电网技术发展，能源市场呈现高度动态化与不确定性特征。传统基于规则的交易策略难以适应复杂市场环境，而Q-learning算法凭借其无模型学习、动态适应性和鲁棒性优势，成为优化能源交易决策的重要工具。本文系统阐述Q-learning算法原理，构建面向能源市场的马尔可夫决策过程（MDP）模型，通过仿真实验验证其在电力交易、微电网运营等场景中的效益优化能力，并提出深度强化学习、多