一、出发点

用简单的熟悉的多项式来近似代替复杂的函数：

• 易计算函数值，导数与积分仍是多项式；
• 多项式由它的系数完全确定，其系数又由它在一点的函数值及其导数所确定。
  

二、泰勒公式的微分基础

回忆微分的概念：若$f^{\prime }(x_0)$存在，在$x_0$附近有
$f(x_0+\Delta x)-f(x_0)\approx f^{\prime }(x_0)\Delta x$，
进一步可得到
$f(x)=f(x_0)+f^{\prime }(x_0)(x-x_0)+o(x-x_0)$，
近似可得
$f(x)\approx f(x_0)+f^{\prime }(x_0)(x-x_0)$。

三、以直代曲

当$|x|$很小时，可通过“以直代曲”实现简单近似：

• $e^x\approx 1+x$
• $\ln (1+x)\approx x$

对应的近似直线为：

• $y=x$（对应$\ln (1+x)\approx x$的近似直线）
• $y=1+x$（对应$e^x\approx 1+x$的近似直线）
  

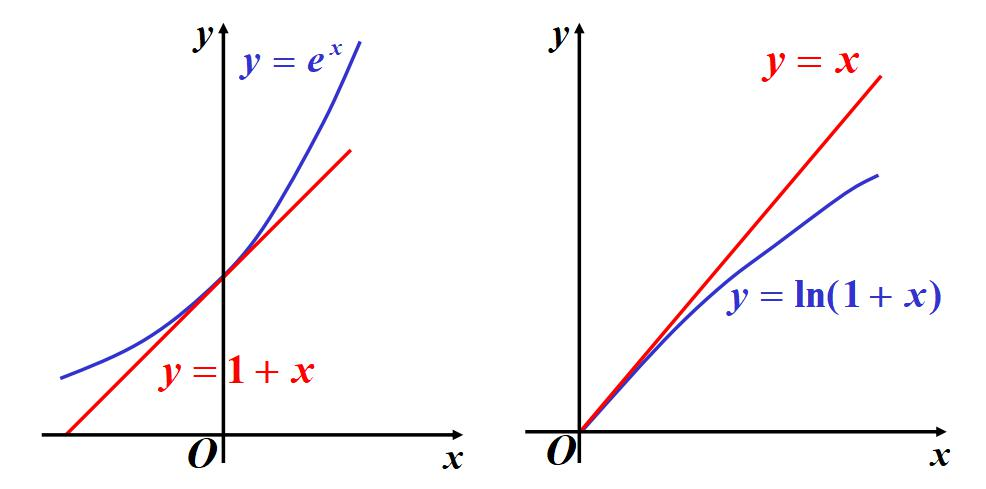
四、一点一世界

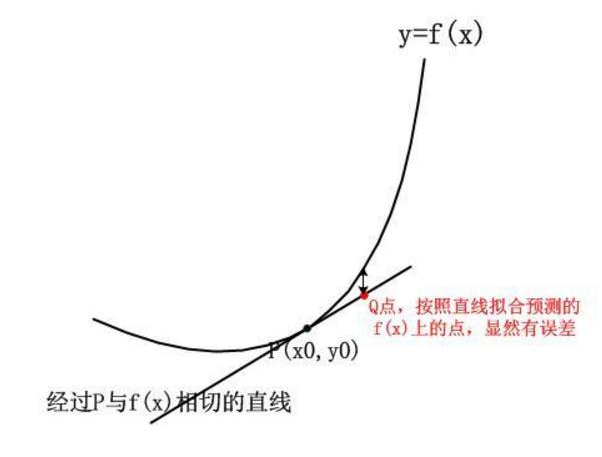
1. 一阶导数的局限性

仅用一阶导数构建的线性近似存在误差：

• 设曲线$y=f(x)$上有一点$P(x_0,y_0)$，经过$P$且与$f(x)$相切的直线为线性近似直线；
• 若用该直线预测曲线$y=f(x)$上的$Q$点（$Q$为$P$附近的点），会明显存在误差；
• 一阶导数仅能判断曲线在$P$点附近的上升（$f^{\prime }(x_0)>0$）或下降（$f^{\prime }(x_0)<0$）趋势，无法把控后续的弯曲走向。
  
  
  

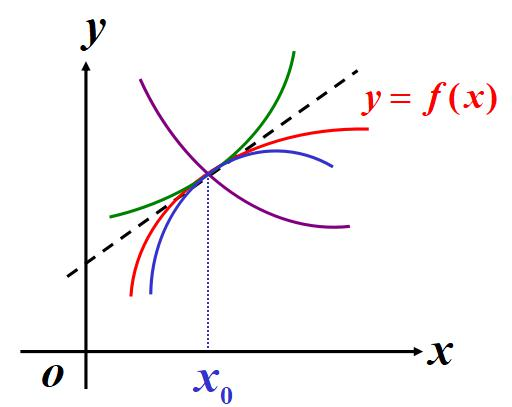
2. 引入二阶导数提升精度

若利用二阶导数，可进一步确定曲线的弯曲方向，减小近似误差：

• 以$P(x_0,y_0)$为原点，将坐标系用两根红线分割为4个区域；
• 若$y$的2阶导数$f^{\prime \prime }(x_0)>0$，则$y=f(x)$在$P$点附近的下一个邻接点位于两根红线围成的某一区域；
• 若$y$的2阶导数$f^{\prime \prime }(x_0)<0$，则$y=f(x)$在$P$点附近的下一个邻接点位于另一区域。

3. 多项式与函数的高阶匹配条件

要让多项式$P_n(x)$精准逼近$f(x)$，需满足以下匹配条件：

1. 函数值匹配：$P_n(x_0)=f(x_0)$；
2. 切线匹配（一阶导数匹配）：$P_n^{\prime }(x_0)=f^{\prime }(x_0)$；
3. 弯曲方向匹配（二阶导数及更高阶导数匹配）：$P_n^{\prime \prime }(x_0)=f^{\prime \prime }(x_0)$，$\cdots$，$P_n^{(n)}(x_0)=f^{(n)}(x_0)$。
   

五、泰勒多项式

满足上述高阶匹配条件的多项式称为$f(x)$在$x_0$处关于$(x-x_0)$的$n$阶泰勒多项式，其表达式为：
$$\begin{array}{rl}{P}_n(x)& =f\left(x_0\right)+f^{\prime }\left(x_0\right)\left(x-x_0\right)+\frac{f^{\prime \prime }\left(x_0\right)}{2!}{\left(x-x_0\right)}^2+\\ & \cdots +\frac{f^{(n)}\left(x_0\right)}{n!}{\left(x-x_0\right)}^n\end{array}$$

六、麦克劳林公式

当$x_0=0$时，泰勒公式称为麦克劳林公式，完整形式（含拉格朗日余项）为：
$$\begin{array}{rl}f(x)& =f(0)+f^{\prime }(0)x+\frac{f^{\prime \prime }(0)}{2!}{x}^2+\cdots +\frac{f^{(n)}(0)}{n!}{x}^n\\ & +\frac{f^{(n+1)}(\theta x)}{(n+1)!}{x}^{n+1}(0<\theta <1)\end{array}$$

忽略余项后，可得麦克劳林近似公式：
$$f(x)\approx f(0)+f^{\prime }(0)x+\frac{f^{\prime \prime }(0)}{2!}{x}^2+\cdots +\frac{f^{(n)}(0)}{n!}{x}^n$$

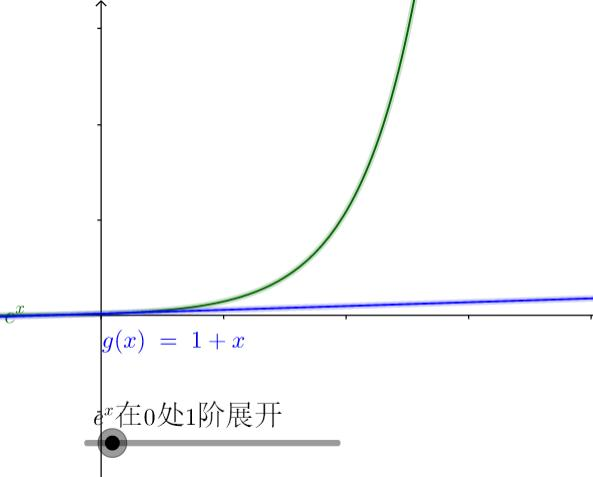
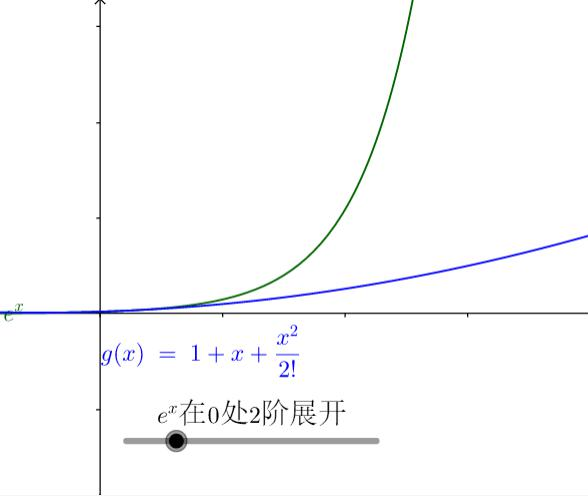
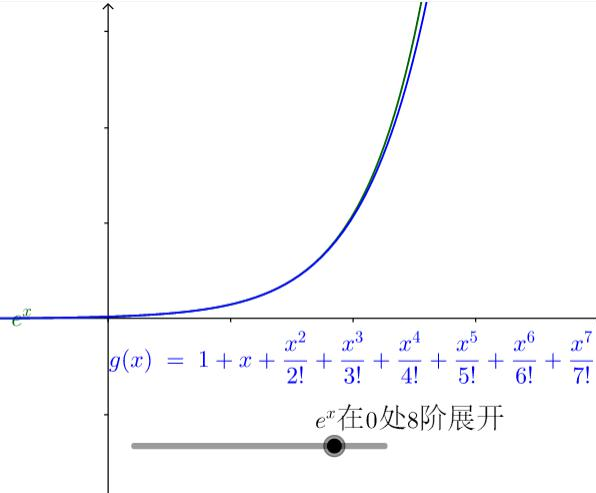
七、多项式逼近示例（以$e^x$为例）

通过不同阶数的麦克劳林多项式逼近$e^x$：

• 0处1阶展开：$g(x)=1+2x$（线性近似）；
  

• 0处2阶展开：$e^x\approx 1+x+\frac{x^2}{2!}$；
  

• 0处3阶展开：$e^x\approx 1+x+\frac{x^2}{2!}+\frac{x^3}{3!}$；
  

• 0处8阶展开：$e^x\approx 1+x+\frac{x^2}{2!}+\cdots +\frac{x^8}{8!}$。
  

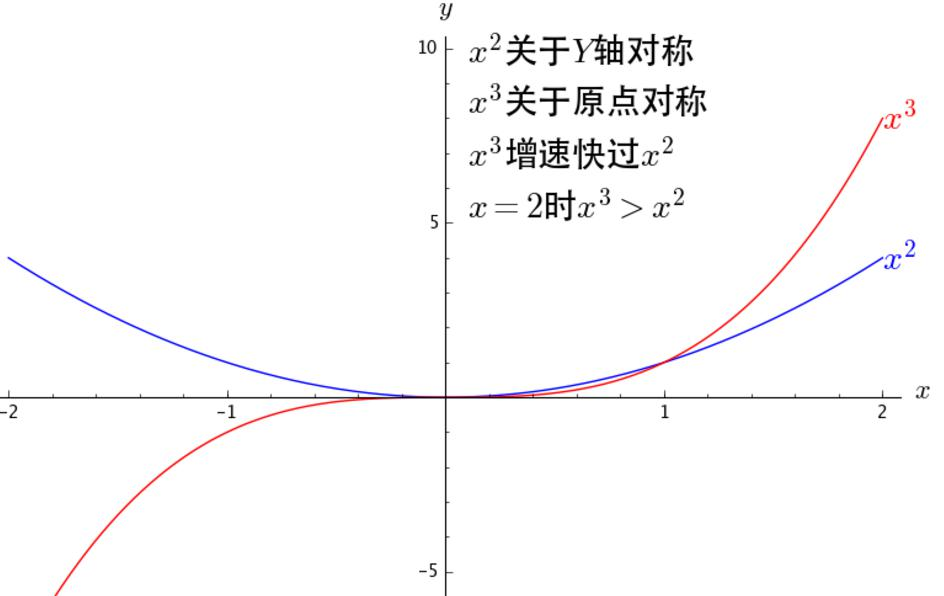
八、阶数的含义

1. 增长速度：多项式的阶数越高，其增长速度越快（如$x^3$增速快于$x^2$，当$x=2$时，$x^3>x^2$）；
2. 影响范围：
   • 低阶项（如$x^2$）对函数在“当前点附近”的描述更精准；
   • 高阶项（如$x^9$）对函数“远离当前点的走势”影响更大（越偏右侧，高阶项影响越显著）；
3. 对称性：
   • 偶次项（如$x^2$）关于$y$轴对称；
   • 奇次项（如$x^3$）关于原点对称。
     

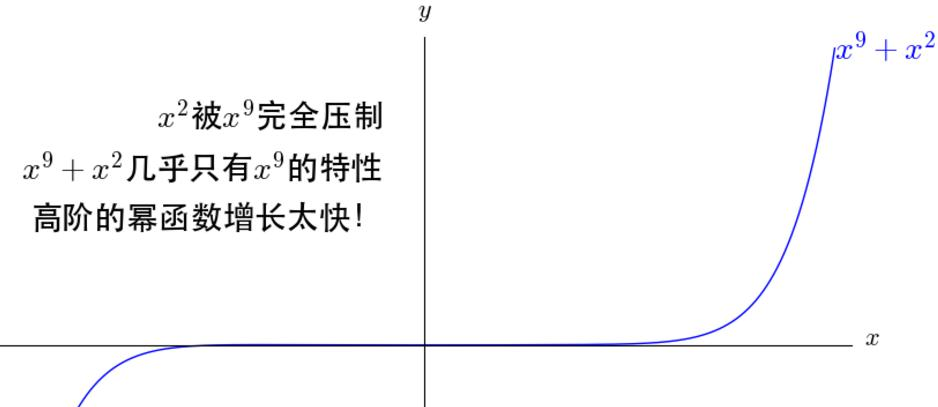
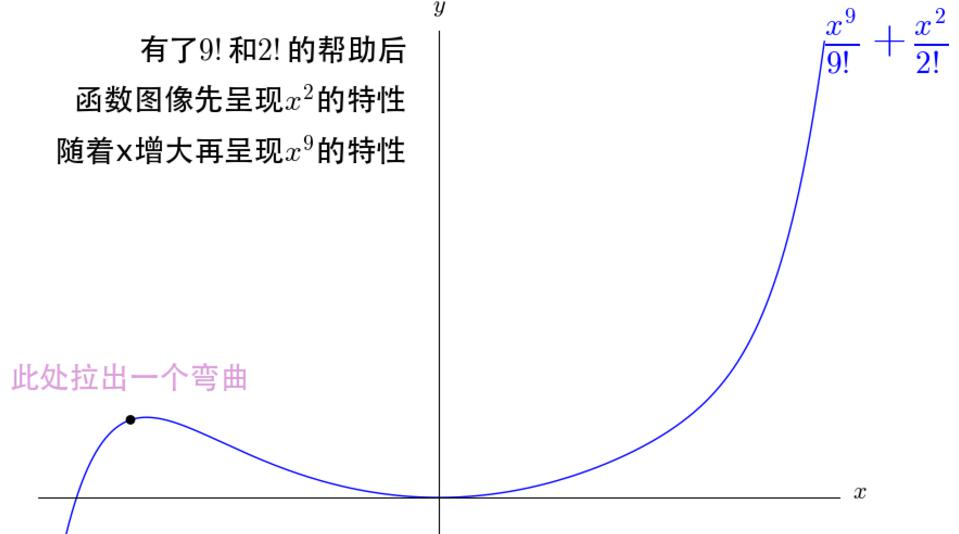
九、阶乘的含义

阶乘（$n!$）的核心作用是平衡高阶项的增长速度，避免高阶项过早压制低阶项：

• 若直接将$x^9$与$x^2$相加（无阶乘），$x^2$会被$x^9$完全压制，$x^9+x^2$几乎仅呈现$x^9$的特性；
  

• 引入阶乘后（如$9!$和$2!$），函数图像会先呈现$x^2$的特性（低阶主导），随着$x$增大，再逐步过渡到$x^9$的特性（高阶主导），实现“渐进式逼近”。
  

十、多项式逼近$\sin x$

$\sin x$的低阶麦克劳林逼近公式为：
$$\sin x\approx x-\frac{x^3}{3!}$$
其图像可通过该多项式初步逼近$y=\sin x$的曲线形态。

十一、示例：麦克劳林展开式计算

例1：求$e^x$的$n$阶麦克劳林展开式

1. 求各阶导数：$f^{\prime }(x)=f^{\prime \prime }(x)=\cdots =f^{(n)}(x)=e^x$；
2. 代入$x=0$：$f(0)=f^{\prime }(0)=f^{\prime \prime }(0)=\cdots =f^{(n)}(0)=1$；
3. 代入麦克劳林公式：
   $$\begin{array}{rl}{e}^x& =1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots +\frac{x^n}{n!}\\ & +\frac{e^{\theta x}}{(n+1)!}{x}^{n+1}(0<\theta <1)\end{array}$$

例2：求$\sin x$的$n$阶麦克劳林展开式

1. 求各阶导数：

   • $f(x)=\sin x$，$f^{\prime }(x)=\cos x$，$f^{\prime \prime }(x)=-\sin x$，$f^{\prime \prime \prime }(x)=-\cos x$，$f^{(4)}(x)=\sin x$，$\cdots$；
   • 一般形式：$f^{(n)}(x)=\sin \left(x+n\cdot \frac{\pi }{2}\right)$；
   • 余项导数：$f^{(n+1)}(\theta x)=\sin \left(\theta x+\frac{n+1}{2}\cdot \pi \right)$。

2. 令$n=2m$（$\sin x$为奇函数，偶次项系数为0），代入麦克劳林公式：
   $$\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots +(-1{)}^{m-1}\frac{x^{2m-1}}{(2m-1)!}+R_{2m}(x)$$
   其中，拉格朗日余项为：
   $$R_{2m}(x)=\frac{(-1{)}^m\cos (\theta x)}{(2m+1)!}{x}^{2m+1}(0<\theta <1)$$