1、AVL树(平衡二叉树)的定义

平衡二叉树 全称叫做 平衡二叉搜索（排序）树，简称 AVL树。英文：Balanced Binary Tree （BBT），注：二叉查找树(BST)

AVL 什么意思 ？
AVL 是大学教授 G.M. Adelson-Velsky 和 E.M. Landis 名称的缩写，他们提出的平衡二叉树的概念，为了纪念他们，将 平衡二叉树 称为 AVL树。

AVL树本质上是一颗二叉查找树，但是它又具有以下特点：

• 它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，
• 左右两个子树 也都是一棵平衡二叉树。

在AVL树中，任何节点的两个子树的高度最大差别为 1 ，所以它也被称为平衡二叉树 。

1.1、平衡因子（Balance Factor，简写为bf）

平衡因子（bf）：结点的左子树的深度减去右子树的深度。
即： 结点的平衡因子 = 左子树的高度 - 右子树的高度 。

在 AVL树中，所有节点的平衡因子都必须满足： -1<=bf<=1;

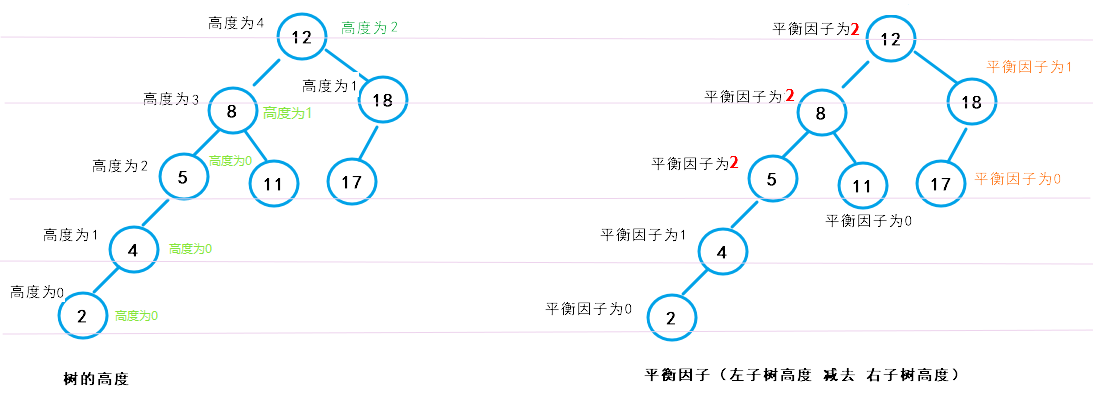
1.2、学习计算每个节点的高度和平衡因子

下图的二叉树，计算每个节点的高度和平衡因子。图示如下：

由 AVL树的定义可知，上面的两个图都不是 AVL树（平衡二叉树） 。

1.3、区分是否是平衡二叉树

下面是平衡二叉树和非平衡二叉树对比的例图：

2、AVL树的作用：

我们知道，对于一般的二叉搜索树（Binary Search Tree），其期望高度（即为一棵平衡树时）为log2n，其各操作的时间复杂度（O(log2n)）同时也由此而决定。但是，在某些极端的情况下（如在插入的序列是有序的时），二叉搜索树将退化成近似链或链，此时，其操作的时间复杂度将退化成线性的，即O(n)。我们可以通过随机化建立二叉搜索树来尽量的避免这种情况，但是在进行了多次的操作之后，由于在删除时，我们总是选择将待删除节点的后继代替它本身，这样就会造成总是右边的节点数目减少，以至于树向左偏沉。这同时也会造成树的平衡性受到破坏，提高它的操作的时间复杂度。

例如：我们按顺序将一组数据 1,2,3,4,5,6 分别插入到一颗空二叉查找树和AVL树中，插入的结果如下图：

由上图可知，同样的结点，由于插入方式不同导致树的高度也有所不同。特别是在带插入结点个数很多且正序的情况下，会导致二叉树的高度是O(N)，而AVL树就不会出现这种情况，树的高度始终是O(lgN).高度越小，对树的一些基本操作的时间复杂度就会越小。这也就是我们引入AVL树的原因。

3、AVL树的基本操作

AVL树的操作基本和二叉查找树一样，这里我们关注的是两个变化很大的操作：插入和删除！

我们知道，AVL树不仅是一颗二叉查找树，它还有其他的性质。如果我们按照一般的二叉查找树的插入方式可能会破坏AVL树的平衡性。同理，在删除的时候也有可能会破坏树的平衡性，所以我们要做一些特殊的处理，包括：单旋转和双旋转！

3.1、插入—— 左左型的右旋：

由上图可知：在插入之前树是一颗AVL树，而插入结点之后，T的左右子树高度差的绝对值不再 <= 1，此时AVL树的平衡性被破坏，我们要对其进行旋转。

在结点T的 左结点（L） 的 左子树（L） 上做了插入元素的操作，我们称这种情况为 左左型 ，我们应该进行右旋转。

注： T 表示 平衡因子(bf)大于1的节点。

3.1.1、右旋的具体步骤：

• T向右旋转成为L的右结点
• L的右节点Y 放到 T的左孩子上

旋转中心是根节点T的左节点（L）。

这样即可得到一颗新的AVL树，旋转过程图如下：

3.1.2、右旋的动画演示：

3.1.3、右旋示例：

示例1：

左左情况下，插入新数据1 时，进行右旋操作：

示例2：

插入 节点2后，进行右旋转：

3.2、插入——左右型的左右旋：

由上图可知，我们在T结点的左结点的右子树上插入一个元素时，会使得根为T的树的左右子树高度差的绝对值不再 <= 1，如果只是进行简单的右旋，得到的树仍然是不平衡的。

在结点T的 左结点（L） 的 右子树（R） 上做了插入元素的操作，我们称这种情况为 左右型 ，我们应该进行左右旋。

注： T 表示 平衡因子(bf)大于1的节点。

3.2.1、左右旋的两次旋转步骤：

第1次是左旋转：

• L节点 左旋转，成为R的左节点
• R的左节点（Y1） 左旋转，成为 L的右节点（即左子节点左转）

第2次是右旋转：

• T节点 右旋转，成为R的右节点
• R的右节点（Y2）右旋转，成为T的左节点（即右子节点右转）

旋转中心是根节点 T 的左节点（R）。

3.2.2、左右旋转的示例：

一定要先把上面的左左型、左右型的旋转搞明白了， 下面的右右型、右左型的旋转就容易理解了。

3.3、插入——右右型的左旋：

由上图可知：在插入之前树是一颗AVL树，而插入新结点之后，T的左右子树高度差的绝对值不再 <+ 1，此时AVL树的平衡性被破坏，我们要对其进行旋转。

在结点T的 右结点（R） 的 右子树（R） 上做了插入元素的操作，我们称这种情况为 右右型 ，我们应该进行左旋转。

注： T 表示 平衡因子(bf)大于1的节点。

3.3.1、左旋的具体步骤：

• T向左旋转成为R的左结点
• R的左节点Y放到T的右孩子上

旋转中心是根节点T的右节点（R）。

这样即可得到一颗新的AVL树，旋转过程图如下：

3.3.2、动画演示：

3.3.3、左旋举例：

示例1：

右右情况下，插入新数据时，左旋操作：

示例2：

3.4、插入——右左型的右左旋：

由上图可知，我们在T结点的右结点的左子树上插入一个元素时，会使得根为T的树的左右子树高度差的绝对值不再 < 1，如果只是进行简单的左旋，得到的树仍然是不平衡的。

在结点T的 右结点（R） 的 左子树（L） 上做了插入元素的操作，我们称这种情况为 右左型 ，我们应该进行右左旋。

注： T 表示 平衡因子(bf)大于1的节点。

3.4.1、右左旋的两次旋转步骤：

第1次是右旋转：

• R 节点 右旋转，成为L的右节点
• L的右节点（Y2） 右旋转，成为R的左节点（即右子节点右转）

第2次是左旋转：

• T 节点 左旋转，成为L的左节点
• L的左节点（Y1）左旋转，成为T的右节点 （即左子节点左转）

旋转中心是根节点 T 的右节点（L）。

3.4.2、右左旋的的示例

4、总结：

在插入的过程中，会出现一下四种情况破坏AVL树的特性，我们可以采取如下相应的旋转。

插入位置	状态	操作
在结点T的左结点（L）的 左子树（L） 上做了插入元素	左左型	右旋
在结点T的左结点（L）的 右子树（R） 上做了插入元素	左右型	左右旋
在结点T的右结点（R）的 右子树（R） 上做了插入元素	右右型	左旋
在结点T的右结点（R）的 左子树（L） 上做了插入元素	右左型	右左旋

注意：
T 表示 平衡因子(bf)大于1的节点。

不知道大家发现规律没，这个规则还是挺好记，下面来个图示：

5、参考文章

https://www.cnblogs.com/idreamo/p/8308336.html

https://segmentfault.com/a/1190000006123188

https://blog.csdn.net/sjg_sjk/article/details/80332151

https://blog.csdn.net/FreeeLinux/article/details/52204851