第六讲 幂级数的收敛半径和收敛域
·
一,函数项级数
- 定义:
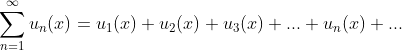 ,
,
- 部分和:
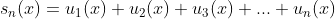
- 收敛点
 :使函数项级数
:使函数项级数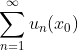 收敛的点
收敛的点 - 发散点
 :使函数项级数
:使函数项级数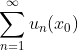 发散的点
发散的点 - 收敛域:D={

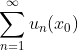 收敛},即所有收敛点的集合
收敛},即所有收敛点的集合 - 和函数:
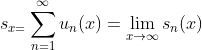 ,
,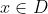
- 余项:
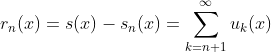
二,幂级数及其收敛性
- 幂级数
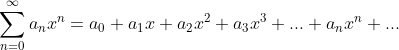
- 有一个明显的收敛点:x=0
- 幂级数是否收敛,跟
的形式相关
- 幂级数的收敛有三种可能:
- 处处绝对收敛,如
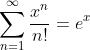
- 仅在x=0处收敛,如
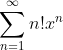
- 在以x=0为中心,两边对称的区间内收敛,如
,收敛域(-1,1)
三,Abel定理
- 设幂级数
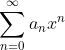 在点
在点 处收敛,则对任何点x:
处收敛,则对任何点x: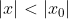 ,幂级数
,幂级数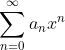 都绝对收敛。如图:
都绝对收敛。如图: 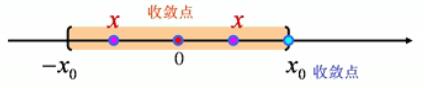
- 设幂级数
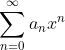 在点
在点 处发散,则对任何点x:
处发散,则对任何点x:,幂级数
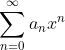 都发散。如图:
都发散。如图: 
四,收敛半径
- 设R是收敛域的上确界
- 由Abel定理,当
,
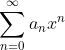 绝对收敛,当
绝对收敛,当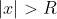 ,
,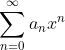 发散
发散 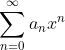 的绝对收敛区间:
的绝对收敛区间: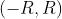
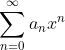 的发散区间:
的发散区间: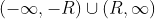
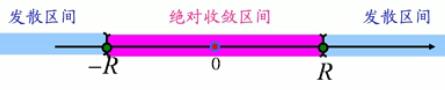
- R即收敛半径,
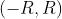 为收敛区间
为收敛区间 - 如果幂级数是
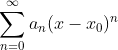 ,则收敛区间是
,则收敛区间是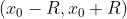
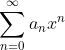 在端点
在端点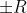 处敛散性不确定
处敛散性不确定
五,求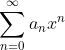 收敛半径R
收敛半径R
- 设正项级数系数的比值
,(
)
- 也可以用正项级数的比值审敛法或根值审敛法求解
- 若
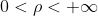 ,则
,则 - 若
 ,则
,则,处处收敛
- 若
 ,则
,则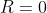 ,仅在x=0处收敛
,仅在x=0处收敛 - 如果幂级数是
,
,则
![R=\frac{1}{\sqrt[m]{\rho }}](https://i-blog.csdnimg.cn/blog_migrate/01fb7436cc13c504b5219263e53631e7.gif)
六,求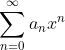 的收敛域(讨论
的收敛域(讨论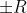 处敛散性)
处敛散性)
- 收敛域有四种可能:
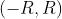 ,
,,
![(-R,R]](https://i-blog.csdnimg.cn/blog_migrate/85987786f3d32082223493c33fd3bad2.gif) ,
, - 将
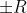 代入
代入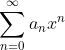 ,分别求
,分别求 和
和的敛散性
- 幂级数只可能在
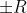 处条件收敛
处条件收敛
阅读全文
AI总结
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容










所有评论(0)