统计判别之模式分类(一)
模式识别的目的就是要确定某一个给定的模式样本属于哪一类。可以通过对被识别对象的多次观察和测量,构成特征向量,并将其作为某一个判决规则的输入,按此规则来对样本进行分类。 在获取模式的观测值时,有些事物具有确定的因果关系,即在一定的条件下,它必然会发生或必然不发生。例如识别一块模板是不是直角三角形,只要凭“三条直线边闭合连线和一个直角”这个特征,测量它是否有三条直线边的闭合连线并有一个直角
贝叶斯判别原则


其中,l12称为似然比,P(ω2)/P(ω1)=θ21称为似然比的判决阈值,此判别称为贝叶斯判别。
•例子(地震预测)
对某一地震高发区进行统计,地震以ω1类表示,正常以ω2类表示
统计的时间区间内,每周发生地震的概率为20%,即P(ω1)=0.2,当然P(ω2)=1-0.2=0.8在任意一周,要判断该地区是否会有地震发生。显然,因为P(ω2)>P(ω1),只能说是正常的可能性大。如要进行判断,只能其它观察现象来实现。通常地震与生物异常反应之间有一定的联系。若用生物是否有异常反应这一观察现象来对地震进行预测,生物是否异常这一结果以模式x代表,这里x为一维特征,且只有x=“异常”和x=“正常”两种结果。


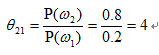
贝叶斯最小风险判别
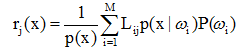
若i≠j,即判别错误,失分, Lij应取正值。
选M=2,即全部的模式样本只有ω1和ω2两类,要求分类器将模式样本分到ω1和ω2两类中,则平均风险可写成:
当分类器将x判别为ω1时:

当分类器将x判别为ω2时:

若r1(x)<r2(x),则x被判定为属于ω1,此时:
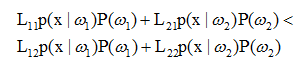
即
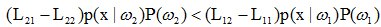
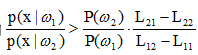
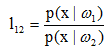
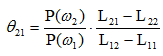
(1) 若l12(x)>θ21,则 x属于w1.
(2) 若l12(x)<θ21,则 x属于w2.
(3) 若l12(x)=θ21,则可做任意判别。
通常,当判别正确时,不失分,可选常数L11=L22=0;判别错误时,可选L12=L21=1:
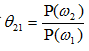
两类(M=2)情况的贝叶斯最小风险判别实例
如图所示为一信号通过一受噪声干扰的信道。
信道输入信号为0或1,噪声为高斯型,其均值μ=0,方差为б2。信道输出为x,试求最优的判别规则,以区分x是0还是1。设送0为ω1类,送1为ω2类,从观察值x的基础上判别它是0还是1。直观上可以看出,若x<0.5应判为0,x>0.5应判为1。用贝叶斯判别条件分析:设信号送0的先验概率为P(0),送1的先验概率为P(1),L的取值为:
这里a1和a2分别对应于输入状态为0和1时的正确判别,L12对应于实际上是ω1类但被判成ω2类(a2)时的代价,L21对应于实际上是ω2类但被判成ω1类(a1)时的代价。正确判别时L取0。当输入信号为0时,受噪声为正态分布N(0,б2)的干扰,其幅值大小的概率密度为:
当输入信号为1时:
则似然比为:
若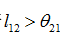
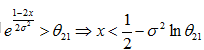
若取L21=L12=1,P(1)=P(0),则x<1/2判为0。若无噪声干扰,即б2=0,则x<1/2判为0。
多类(M类)情况的贝叶斯最小风险判别
对于M类情况,若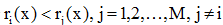
L可如下取值(仍按判对失分为0,判错失分为1记):
则条件平均风险可写成:
 ,有当
,有当
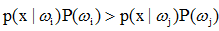 时,x属于w1,对应于判别函数为:取
时,x属于w1,对应于判别函数为:取
 ,则对于全部
,则对于全部
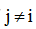 的值,若
的值,若
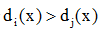 ,则x属于w1。
,则x属于w1。
下一节将介绍正态分布模式的贝叶斯分类器。
更多推荐
 已为社区贡献5条内容
已为社区贡献5条内容

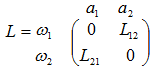

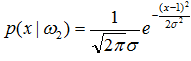
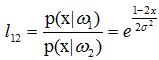

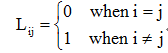
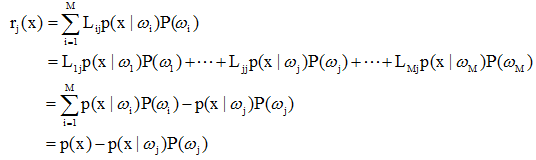





所有评论(0)