Python机器学习库sklearn里利用LR模型进行三分类(多分类)的原理
有关LR模型的完整理论知识参考http://blog.csdn.net/cymy001/article/details/78153036首先,LR将线性模型利用sigmoid函数进一步做了非线性映射。将分类超平面两侧的正负样本点,通过压缩函数转化成了以0.5为分解的两类:类别0和类别1。这个转化过程见下图:上图给出的是线性边界与LR分布函数(即sigmoid函数)的...
·
有关LR模型的完整理论知识参考http://blog.csdn.net/cymy001/article/details/78153036
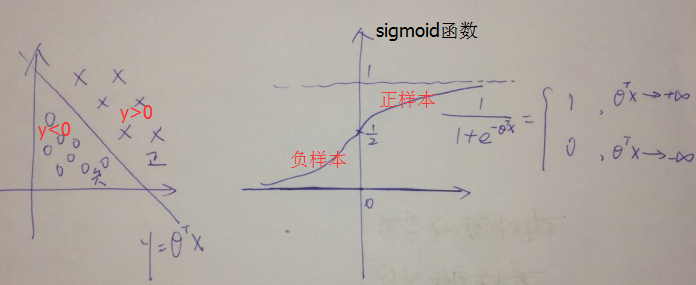
首先,LR将线性模型利用sigmoid函数进一步做了非线性映射。
将分类超平面两侧的正负样本点,通过压缩函数转化成了以0.5为分解的两类:类别0和类别1。
这个转化过程见下图:
上图给出的是线性边界与LR分布函数(即sigmoid函数)的映射对应关系;同样,对于非线性判定边界sigmoid函数也使用,如下图:
然后,再考虑如何去获得模型参数,就是判定边界的参数怎么获得,这里是利用MLE进行求解的,具体求解过程参考本文最初给的理论链接地址。
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(z):
return 1.0 / (1.0 + np.exp(-z))
z = np.arange(-7, 7, 0.1)
phi_z = sigmoid(z)
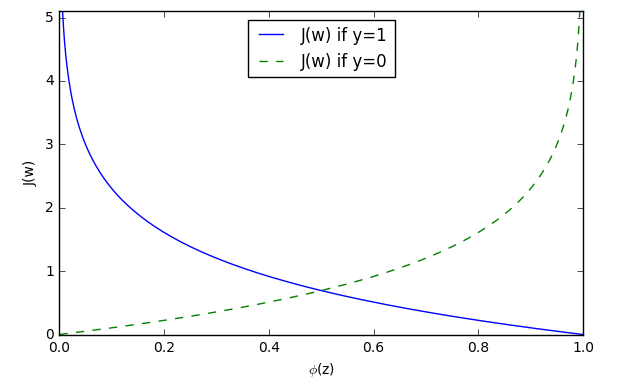
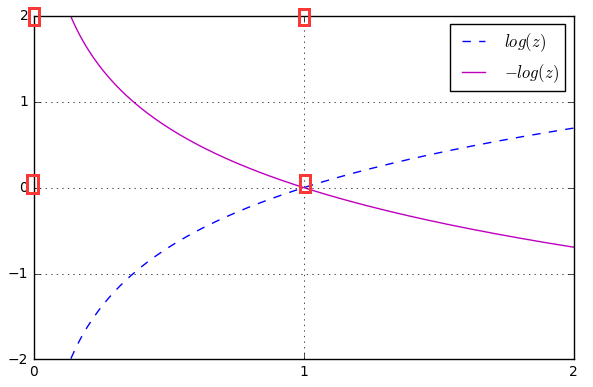
def cost_1(z):
return - np.log(sigmoid(z))
def cost_0(z):
return - np.log(1 - sigmoid(z)) #这里cost_1(z)和cost_0(z)对应上述公式
z = np.arange(-10, 10, 0.1)
phi_z = sigmoid(z)
c1 = [cost_1(x) for x in z]
plt.plot(phi_z, c1, label='J(w) if y=1')
c0 = [cost_0(x) for x in z]
plt.plot(phi_z, c0, linestyle='--', label='J(w) if y=0')
plt.ylim(0.0, 5.1)
plt.xlim([0, 1])
plt.xlabel('$\phi$(z)')
plt.ylabel('J(w)')
plt.legend(loc='best')
plt.tight_layout()
# plt.savefig('./figures/log_cost.png', dpi=300)
plt.show()
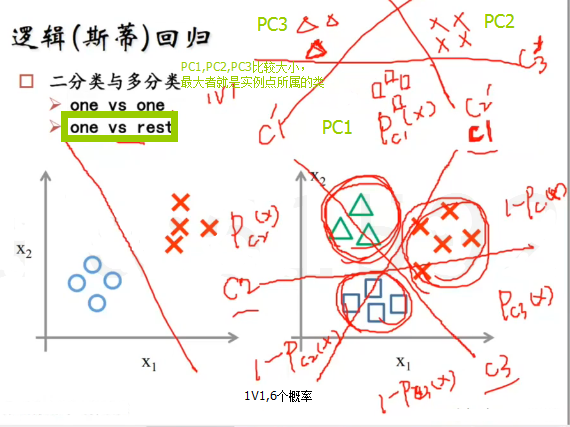
最后,考虑LR进行三分类(多分类)时,是特征的线性组合和sigmoid函数复合的函数进行概率计算和分类的。
from IPython.display import Image
%matplotlib inline
# Added version check for recent scikit-learn 0.18 checks
from distutils.version import LooseVersion as Version
from sklearn import __version__ as sklearn_version
from sklearn import datasets
import numpy as np
iris = datasets.load_iris() #http://scikit-learn.org/stable/auto_examples/datasets/plot_iris_dataset.html
X = iris.data[:, [2, 3]]
y = iris.target #取species列,类别
if Version(sklearn_version) < '0.18':
from sklearn.cross_validation import train_test_split
else:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=0) #train_test_split方法分割数据集
from sklearn.preprocessing import StandardScaler
sc = StandardScaler() #初始化一个对象sc去对数据集作变换
sc.fit(X_train) #用对象去拟合数据集X_train,并且存下来拟合参数
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)
from sklearn.linear_model import LogisticRegression
def sigmoid(z):
return 1.0 / (1.0 + np.exp(-z))
lr = LogisticRegression(C=1000.0, random_state=0)
#http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html#sklearn.linear_model.LogisticRegression
lr.fit(X_train_std, y_train)
lr.predict_proba(X_test_std[0, :].reshape(1, -1)) #计算该预测实例点属于各类的概率
#Output:array([[ 2.05743774e-11, 6.31620264e-02, 9.36837974e-01]])
#验证predict_proba的作用
c=lr.predict_proba(X_test_std[0, :].reshape(1, -1))
c[0,0]+c[0,1]+c[0,2]
#Output:0.99999999999999989
#查看lr模型的特征系数
lr = LogisticRegression(C=1000.0, random_state=0)
#http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html#sklearn.linear_model.LogisticRegression
lr.fit(X_train_std, y_train)
print(lr.coef_)
#Output:[[-7.34015187 -6.64685581]
# [ 2.54373335 -2.3421979 ]
# [ 9.46617627 6.44380858]]
#验证predict_proba工作原理
Zz=np.dot(lr.coef_,X_test_std[0, :].T)+lr.intercept_
np.array(sigmoid(Zz))/sum(np.array(sigmoid(Zz)))
#Output:array([ 2.05743774e-11, 6.31620264e-02, 9.36837974e-01])
#此结果就是预测实例点各类的概率
点击阅读全文
更多推荐
 已为社区贡献8条内容
已为社区贡献8条内容

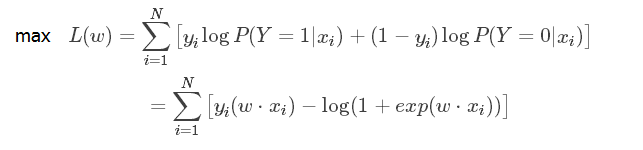





所有评论(0)