机器学习 回归分析(regression analysis)
____tz_zs学习笔记监督学习(Supervised Learning)监督学习中,如果预测的变量是离散的,我们称其为分类(如决策树,支持向量机等),如果预测的变量是连续的,我们称其为回归。回归(Regression):Y变量为连续数值型(continuous numerical variable)如:房价,人数,降雨量分类(Classification): Y变量为类别型(categoric
____tz_zs学习笔记
监督学习(Supervised Learning)
监督学习中,如果预测的变量是离散的,我们称其为分类(如决策树,支持向量机等),如果预测的变量是连续的,我们称其为回归。
回归(Regression):Y变量为连续数值型(continuous numerical variable)
如:房价,人数,降雨量
分类(Classification): Y变量为类别型(categorical variable)
如:颜色类别,电脑品牌,有无信誉
回归分析(regression analysis)
建立方程模拟两个或者多个变量之间的关系的过程
被预测的变量叫做:因变量(dependent variable), y, 输出(output)被用来进行预测的变量叫做: 自变量(independent variable), x, 输入(input)
在统计学中,回归分析(regression analysis)是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。运用十分广泛,回归分析按照涉及的变量的多少,分为一元回归和多元回归分析;按照自变量(百度百科 中这里写的是因变量,个人觉得应该是自变量)的多少,可分为简单回归分析和多重回归分析;按照自变量和因变量之间的关系类型,可分为线性回归分析和非线性回归分析。如果在回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且自变量之间存在线性相关,则称为多重线性回归分析。在大数据分析中,回归分析是一种预测性的建模技术,它研究的是因变量(目标)和自变量(预测器)之间的关系。这种技术通常用于预测分析,时间序列模型以及发现变量之间的因果关系。例如,司机的鲁莽驾驶与道路交通事故数量之间的关系,最好的研究方法就是回归。
提醒:发现很多中文资料里,多元回归、多重回归等的概念及英文单词的对应均有错漏,根据维基百科及一些英文论文,归纳如下:
一般线性模型(General linear model)/多元回归(multivariate regression) 多个自变量,多个因变量,是多重线性回归(Multiple linear regression)的推广。
多重线性回归(Multiple linear regression)是线性回归(linear regression )的推广(多个自变量),是(general linear models)的特例(一个因变量)。
当多元回归模型(multivariate regression model)中有多个预测变量(predictor variable)时,模型为多元多重回归(multivariate multiple regression)。
回归方程(regression equation)
回归方程(regression equation)是根据样本资料通过回归分析所得到的反映一个变量(因变量)对另一个或一组变量(自变量)的回归关系的数学表达式。回归直线方程用得比较多,可以用最小二乘法求回归直线方程中的a,b,从而得到回归直线方程。【所属类型:数学】
简单线性回归(Simple Linear Regression)
简单线性回归包含一个自变量(x)和一个因变量(y),两个变量的关系用一条直线来模拟。
简单线性回归模型
被用来描述因变量(y)和自变量(X)以及偏差(error)之间关系的方程叫做回归模型
简单线性回归的模型是:
其中:β0、β1为参数,ε 为偏差
简单线性回归方程
E(y) = β0+β1x这个方程对应的图像是一条直线,称作回归线
其中,β0是回归线的截距
β1是回归线的斜率
E(y)是在一个给定x值下y的期望值(均值)
估计的简单线性回归方程
ŷ=b0+b1x这个方程叫做估计线性方程(estimated regression line)
其中,b0是估计线性方程的纵截距
b1是估计线性方程的斜率
ŷ是在自变量x等于一个给定值的时候,y的估计值
计算公式:
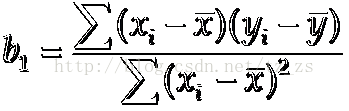
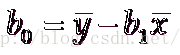
逻辑的代码实现
# -*- coding: utf-8 -*-
"""
@author: tz_zs
"""
import numpy as np
# 传入数据,返回b0,b1的估计值
def fitSLR(x, y):
n = len(x)
dinominator = 0 #分母
numerator = 0 # 分子
for i in range(0, n):
numerator += (x[i] - np.mean(x))*(y[i] - np.mean(y))
dinominator += (x[i] - np.mean(x))**2
print("numerator:"+str(numerator))
print("dinominator:"+str(dinominator))
b1 = numerator/float(dinominator)
b0 = np.mean(y)/float(np.mean(x))
return b0, b1
def predict(x, b0, b1):
return b0 + x*b1
x = [1, 3, 2, 1, 3]
y = [14, 24, 18, 17, 27]
b0, b1 = fitSLR(x, y)
print "intercept:", b0, " slope:", b1
x_test = 6
y_test = predict(6, b0, b1)
print "y_test:", y_test
运行结果:
numerator:20.0
dinominator:4.0
intercept: 10.0 slope: 5.0
y_test: 40.0
多重线性回归(Multiple linear regression,MLR)
多重线性回归(multiple linear regression) 是简单直线回归的推广,研究一个因变量与多个自变量之间的数量依存关系。多重线性回归用回归方程描述一个因变量与多个自变量的依存关系,简称多重回归。
多重回归模型
y=β0+β1x1+β2x2+ ... +βpxp+ε
其中:β0,β1,β2... βp是参数
ε是误差值
多重回归方程
E(y)=β0+β1x1+β2x2+ ... +βpxp
估计多重回归方程:
y_hat=b0+b1x1+b2x2+ ... +bpxp
一个样本被用来计算β0,β1,β2... βp的点估计b0, b1, b2,..., bp
# -*- coding: utf-8 -*-
"""
@author: tz_zs
"""
from numpy import genfromtxt
import numpy as np
from sklearn import datasets,linear_model
'''
要使print全部打印而不省略(http://blog.csdn.net/gzhermit/article/details/72716619)
np.set_printoptions(threshold = 1e6)#设置打印数量的阈值,1e6 = 1000000.0此方法为设置一较大值
或
np.set_printoptions(threshold='nan') #全部输出
'''
np.set_printoptions(threshold='nan') #全部输出
dataPath = r"Delivery.csv"
deliveryData = genfromtxt(dataPath,delimiter=',') # csv文件的分隔符是","
print "deliveryData:"
print deliveryData
X = deliveryData[:,:-1]
Y = deliveryData[:,-1]
print ("X:")
print (X)
print ("Y:")
print (Y)
# 线性回归方程
regr = linear_model.LinearRegression()
regr.fit(X,Y)
print "coefficients"
print regr.coef_
print "intercept: "
print regr.intercept_
xPred = [102, 6]
yPred = regr.predict(xPred)
print "predicted y: "
print yPred
Logistic 回归(Logistic Regression)
logistic回归(Logistic regression) 与多重线性回归实际上有很多相同之处,最大的区别就在于他们的因变量不同,其他的基本都差不多,正是因为如此,这两种回归可以归于同一个家族,即广义线性模型(generalized linear model)。按照因变量的不同,如果是连续的,就是多重线性回归,如果是二项分布,就是logistic回归。
logistic回归的因变量可以是二分非线性差分方程类的,也可以是多分类的,但是二分类的更为常用,也更加容易解释。所以实际中最为常用的就是二分类的logistic回归。
.
# -*- coding: utf-8 -*-
"""
@author: tz_zs
"""
import numpy as np
import random
# m denotes the number of examples here, not the number of features
# 梯度下降策略
def gradientDescent(x, y, theta, alpha, m, numIterations):
xTrans = x.transpose() #转置
for i in range(0, numIterations):
hypothesis = np.dot(x, theta)
loss = hypothesis - y
# avg cost per example (the 2 in 2*m doesn't really matter here.
# But to be consistent with the gradient, I include it)
cost = np.sum(loss ** 2) / (2 * m)
print("Iteration %d | Cost: %f" % (i, cost))
# avg gradient per example
gradient = np.dot(xTrans, loss) / m
# update
theta = theta - alpha * gradient
return theta
# 生成数据 numPoints实例数量,bias偏好,variance方差
def genData(numPoints, bias, variance):
x = np.zeros(shape=(numPoints, 2))
y = np.zeros(shape=numPoints)
# basically a straight line
for i in range(0, numPoints):
# bias feature
x[i][0] = 1
x[i][1] = i
# our target variable
y[i] = (i + bias) + random.uniform(0, 1) * variance
return x, y
# gen 100 points with a bias of 25 and 10 variance as a bit of noise
x, y = genData(100, 25, 10)
m, n = np.shape(x)
numIterations= 100000
alpha = 0.0005
theta = np.ones(n) #theta和实例的维度一致
theta = gradientDescent(x, y, theta, alpha, m, numIterations)
print(theta)
.
梯度下降(gradient decent)
.
.
- α为学习率
- 同时对所有的θ进行更新
- 重复更新直到收敛
.
最小二乘法与梯度下降法
最小二乘法跟梯度下降法都是通过求导来求损失函数的最小值,那它们有什么区别呢。
相同
1.本质相同:两种方法都是在给定已知数据(independent & dependent variables)的前提下对dependent variables算出出一个一般性的估值函数。然后对给定新数据的dependent variables进行估算。
2.目标相同:都是在已知数据的框架内,使得估算值与实际值的总平方差尽量更小(事实上未必一定要使用平方),估算值与实际值的总平方差的公式为:
其中
为第i组数据的independent variable,
为第i组数据的dependent variable,
为系数向量。
不同
实现方法和结果不同:最小二乘法是直接对
求导找出全局最小,是非迭代法。而梯度下降法是一种迭代法,先给定一个
,然后向
下降最快的方向调整
,在若干次迭代之后找到局部最小。梯度下降法的缺点是到最小点的时候收敛速度变慢,并且对初始点的选择极为敏感,其改进大多是在这两方面下功夫。
参考文章:http://www.cnblogs.com/iamccme/archive/2013/05/15/3080737.html
皮尔逊相关系数 (Pearson Correlation Coefficient):
衡量两个值线性相关强度的量取值范围 [-1, 1]:
正向相关: >0, 负向相关:<0, 无相关性:=0
.
R平方值:
定义:决定系数,反应因变量的全部变异能通过回归关系被自变量解释的比例。描述:如R平方为0.8,则表示回归关系可以解释因变量80%的变异。换句话说,如果我们能控制自变量不变,则因变量的变异程度会减少80%
简单线性回归:
R^2 = r * r
多元线性回归:
R平方也有其局限性:R平方随着自变量的增加会变大,R平方和样本量是有关系的。因此,我们要到R平方进行修正。修正的方法:
.
# -*- coding: utf-8 -*-
"""
@author: tz_zs
"""
import numpy as np
from astropy.units import Ybarn
import math
# 计算相关度
def computeCorrelation(X, Y):
xBar = np.mean(X) #均值
yBar = np.mean(Y)
SSR = 0
varX = 0
varY = 0
for i in range(0 , len(X)):
diffXXBar = X[i] - xBar
diffYYBar = Y[i] - yBar
SSR += (diffXXBar * diffYYBar)
varX += diffXXBar**2
varY += diffYYBar**2
SST = math.sqrt(varX * varY)
return SSR / SST
testX = [1, 3, 8, 7, 9]
testY = [10, 12, 24, 21, 34]
print computeCorrelation(testX, testY)
.
回归问题的准确性评价
https://book.douban.com/reading/46607817/
https://www.cnblogs.com/rayshaw/p/8628174.html
建立回归器后,需要建立评价回归器拟合效果的指标模型。
- 平均误差(mean absolute error):这是给定数据集的所有数据点的绝对误差平均值
- 均方误差(mean squared error):给定数据集的所有数据点的误差的平方的平均值,最流行
- 中位数绝对误差(mean absolute error):给定数据集的所有数据点的误差的中位数,可以消除异常值的干扰
- 解释方差分(explained variance score):用于衡量我们的模型对数据集波动的解释能力,如果得分为1.0,表明我们的模型是完美的。
- R方得分(R2 score):读作R方,指确定性相关系数,用于衡量模型对未知样本预测的效果,最好的得分为1.0,值也可以是负数。
import sklearn.metrics as sm
print('mean absolute error=',round(sm.mean_absolute_error(y_test,y_test_pre),2))
print('mean squared error=',round(sm.mean_squared_error(y_test,y_test_pre),2))
print('median absolute error=',round(sm.median_absolute _error(y_test,y_test_pre),2))
print('explained variance score=',round(sm.explained_variance _score(y_test,y_test_pre),2))
print('R2 score=',round(sm.r2_score(y_test,y_test_pre),2))
.
通常情况下,尽量保证均方误差最低,而且解释方差分最高。
.
Python环境下的8种简单线性回归算法
本文中,作者讨论了 8 种在 Python 环境下进行简单线性回归计算的算法,对比了他们的计算复杂度。
更多推荐
 已为社区贡献8条内容
已为社区贡献8条内容
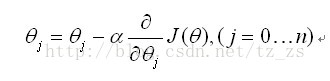
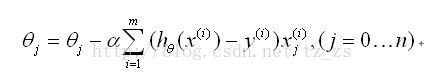
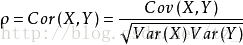
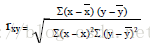
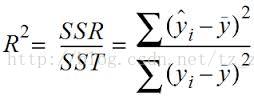
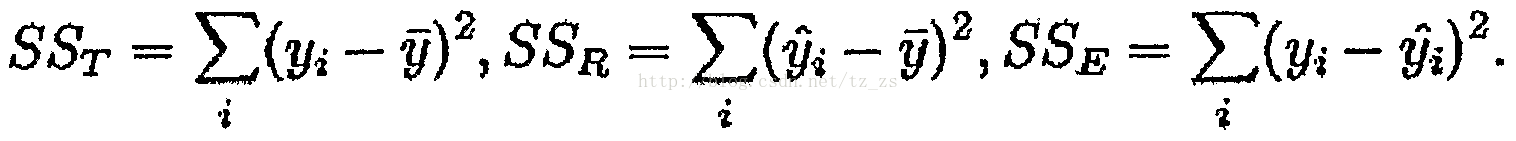









所有评论(0)