特征选择，也就是特征缩减，是通过对损失函数(即优化目标)加入惩罚项，使得训练求解参数过程中会考虑到系数的大小，通过设置缩减系数(惩罚系数)，会使得影响较小的特征的系数衰减到0，只保留重要的特征。嵌入式特征选择方法有：LASSO(L1正则化)和岭回归(L2正则化)。特征选择，可消除噪声特征和消除关联的特征，并能减少训练开销。

对于特征选择，需要关注正则化概念，正则化是对损失函数(目标函数)加入一个惩罚项，使得模型由多解变为更倾向其中一个解，也成为罚函数。在介绍岭回顾和LASSO前，先介绍线性回归。

1、线性归回

对于一个样本 xi ，它的输出值是其特征的线性组合： 

其中， w0 称为截距，或者bias，上式中通过增加 xi0=1 把 w0 也吸收到向量表达中了，简化了形式，因此实际上 xi 有 p+1 维度。

线性回归的目标是用预测结果尽可能地拟合目标label，用最常见的最小平方误差： 

可以直接求出最优解： 

看起来似乎很简单，但是在实际使用的过程中会有不少问题，其中一个主要问题就是上面的协方差矩阵不可逆时，目标函数最小化导数为零时方程有无穷解，没办法求出最优解。尤其在 p>n 时，必然存在这样的问题，这个时候也存在overfitting的问题。这个时候需要对 w

做一些限制，使得它的最优解空间变小，也就是所谓的regularization，正则。

2、岭回归 ridge regeression

最为常见的就是对

w 的模做约束，如ridge regression，岭回归，就是在线性回归的基础上加上 l2 -norm的约束，loss function是（习惯上一般会去掉前面线性回归目标函数中的常数项 1n ，同时为了后面推导的简洁性会加上一个 12 ）： 

有解析解： 

其中 λ>0 是一个参数，有了正则项以后解就有了很好的性质，首先是对 w 的模做约束，使得它的数值会比较小，很大程度上减轻了overfitting的问题；其次是上面求逆部分肯定可以解，在实际使用中ridge regression的作用很大，通过调节参数 λ ，可以得到不同的回归模型。

实际上ridge regression可以用下面的优化目标形式表达： 

也就是说，我依然优化线性回归的目标，但是条件是 w 的模长不能超过限制 θ 。上面两种优化形式是等价的，可以找到一 一对应的 λ 和 θ 。

3、稀疏约束，Lasso

先看一下几种范式(norm)的定义， 

如前面的ridge regression，对 w 做2范式约束，就是把解约束在一个 l2 -ball里面，放缩是对球的半径放缩，因此 w 的每一个维度都在以同一个系数放缩，通过放缩不会产生稀疏的解——即某些 w 的维度是0。而实际应用中，数据的维度中是存在噪音和冗余的，稀疏的解可以找到有用的维度并且减少冗余，提高回归预测的准确性和鲁棒性（减少了overfitting）。在压缩感知、稀疏编码等非常多的机器学习模型中都需要用到稀疏约束。

稀疏约束最直观的形式应该是约束0范式，如上面的范式介绍， w 的0范式是求 w 中非零元素的个数。如果约束 ∥w∥0≤k ，就是约束非零元素个数不大于k。不过很明显，0范式是不连续的且非凸的，如果在线性回归中加上0范式的约束，就变成了一个组合优化问题：挑出 ≤k 个系数然后做回归，找到目标函数的最小值对应的系数组合，是一个NP问题。

有趣的是， l1 -norm（1范式）也可以达到稀疏的效果，是0范式的最优凸近似，借用一张图[1]： 

很重要的是1范式容易求解，并且是凸的，所以几乎看得到稀疏约束的地方都是用的1范式。

回到本文对于线性回归的讨论，就引出了Lasso(least absolute shrinkage and selection operator) 的问题：

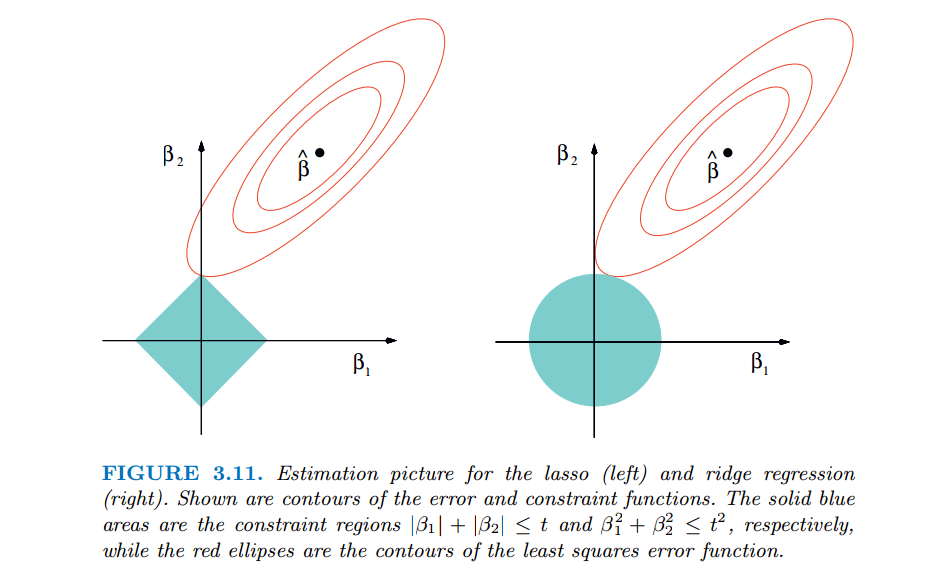
也就是说约束在一个 l1 -ball里面。ridge和lasso的效果见下图：

红色的椭圆和蓝色的区域的切点就是目标函数的最优解，我们可以看到，如果是圆，则很容易切到圆周的任意一点，但是很难切到坐标轴上，因此没有稀疏；但是如果是菱形或者多边形，则很容易切到坐标轴上，因此很容易产生稀疏的结果。这也说明了为什么1范式会是稀疏的。