Sigmoid函数是一个有着优美S形曲线的数学函数，在逻辑回归、人工神经网络中有着广泛的应用。Sigmoid函数的数学形式是：

$$f(x) = \frac{1}{{1 + {e^{ - x}}}}$$
其函数图像如下：

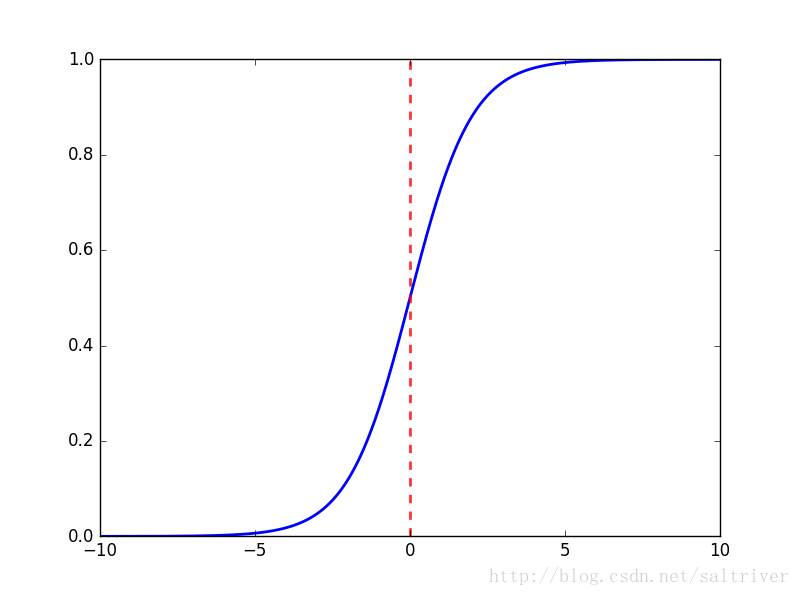
可以看出，sigmoid函数连续，光滑，严格单调，以(0,0.5)中心对称，是一个非常良好的阈值函数。

当x趋近负无穷时，y趋近于0；趋近于正无穷时，y趋近于1；x=0时，y=0.5。当然，在x超出[-6,6]的范围后，函数值基本上没有变化，值非常接近，在应用中一般不考虑。

Sigmoid函数的值域范围限制在(0,1)之间，我们知道[0,1]与概率值的范围是相对应的，这样sigmoid函数就能与一个概率分布联系起来了。

Sigmoid函数的导数是其本身的函数，即$f'(x) = f(x)(1 - f(x))$，计算非常方便，也非常节省计算时间。推导过程如下：
根据常用的求导公式，得到：

$$f'(x) = ( - 1){(1 + {e^{ - x}})^{ - 2}}(0 + ( - 1){e^{ - x}}) = \frac{{{e^{ - x}}}}{{{{(1 + {e^{ - x}})}^2}}} = \frac{{{e^{ - x}}}}{{1 + {e^{ - x}}}}\frac{1}{{1 + {e^{ - x}}}}$$
而：
$$1 - f(x) = 1 - \frac{1}{{1 + {e^{ - x}}}} = \frac{{{e^{ - x}}}}{{1 + {e^{ - x}}}}$$
因此， $f'(x) = f(x)(1 - f(x))$。

虽然sigmoid函数拥有良好的性质，可以用在分类问题上，如作为逻辑回归模型的分类器。但为什么偏偏选用这个函数呢？除了上述的数学上更易处理外，还有其本身的推导特性。
对于分类问题，尤其是二分类问题，都假定是服从伯努利分布。伯努利分布的概率质量函数PMF为：

$$f(x|p) = {p^x}{(1 - p)^{1 - x}}$$
根据《 指数分布族》的一般表达式框架：
$$f(x|\theta ) = h(x)\exp \{ \eta (\theta )T(x) - A(\theta )\}$$
将伯努利分布变形为：
$$f(x|p) = \exp \{ \ln (\frac{p}{{1 - p}})x + \log (1 - p)\}$$
其中： $\theta = p$， $h(x) = 1$， $T(x) = x$， $\eta (\theta ) = \ln \frac{p}{{1 - p}}$， $A(\theta ) = - \ln (1 - p)$。因此，伯努利分布也属于指数分布族。

我们可以推导下$p$和$\eta (\theta )$之间的关系：

$$\eta (\theta ) = \ln \frac{p}{{1 - p}}$$ 则：
$$- \eta (\theta ) = - \ln \frac{p}{{1 - p}} = \ln \frac{{1 - p}}{p} = \ln (\frac{1}{p} - 1)$$ 得到:
$${e^{ - \eta (\theta )}} = \frac{1}{p} - 1$$
$$1 + {e^{ - \eta (\theta )}} = \frac{1}{p}$$
$$p = \frac{1}{{1 + {e^{ - \eta (\theta )}}}}$$
这也就是sigmoid函数形式。