神经网络和深度学习-学习总结
1. 简介 神经网络和深度学习是由Michael Nielsen所写,其特色是:兼顾理论和实战,是一本供初学者深入理解Deep Learning的好书。2. 使用神经网络识别手写数字2.1 感知器(Perceptrons) 感知器工作原理:接收一系列二进制输入,经过特定的规则计算之后,输出一个简单的二进制。 计算规则:通过引入
1. 简介
神经网络和深度学习是由Michael Nielsen所写,其特色是:兼顾理论和实战,是一本供初学者深入理解Deep Learning的好书。
2. 感知器与sigmoid神经元
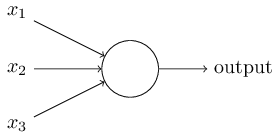
2.1 感知器(Perceptrons)
感知器工作原理:接收一系列二进制输入,经过特定的规则计算之后,输出一个简单的二进制。
计算规则:通过引入权重(weights)表示每个输入对于输出的重要性,则有
记 w⋅x=∑jwjxj ,b=-threshold,则有
其w是权重,b是偏差。
2.2 Sigmoid神经元(Sigmoid Neurons)
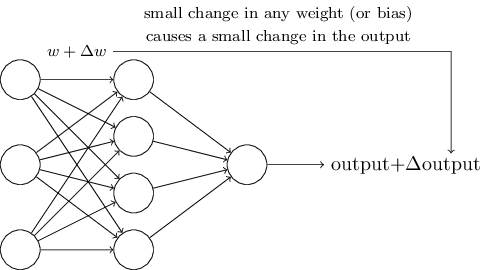
为了使学习变得可能,需要具备的【学习特征】:权重或偏差有较小的变化,导致输出也有较小的变化。如下图所示:
感知器网络存在的缺陷是:某个感知器较小的权重或偏差变化,可能导致输出在0与1之间进行翻转。所以包含感知器的网络不具备【学习特征】。
幸运的是:Sigmoid神经元具有此【学习特征】,即其较小的权重或偏差变化,导致其输出变化较小。
Sigmoid函数:
Sigmoid神经元输出:
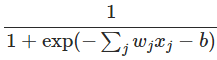
感知器与sigmoid神经元的差别:
1) 感知器只输出0或1
2)sigmoid神经元不只输出0或1,而可输出[0,1]之间的任意值
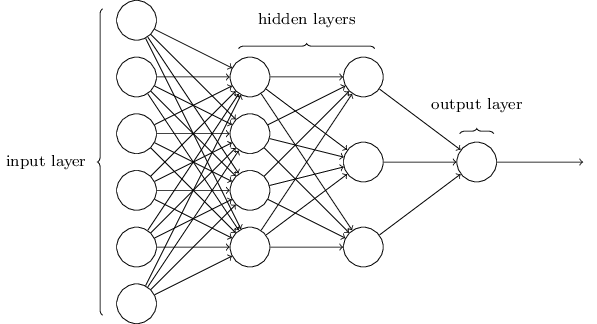
3. 神经网络架构
3.1 手写数字识别
训练图像大小为28x28,每个训练图像有一个手写数字。
在输出层,如果第一个神经元被激活(即其输出接近1),则此网络认为此手写数字为0;
如果第二个神经元被激活(即其输出接近1),则此网络认为此手写数字为1;
其它以此类推。
3.2 算法描述
设x表示训练图像,则x是一个28x28=784维列向量。

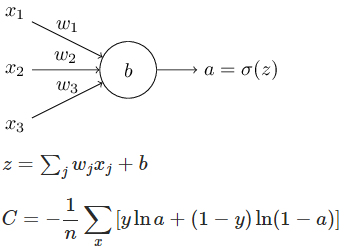
需要寻找一个算法来发现w和b,使其输出接近标签值,为了量化接近程序,定义如下成本函数:
w:所有权重的集合
b:所有偏差的集合
n:训练样本数
a: 输出向量(其值依赖x,w,b)
x:一幅训练图像
||v||:表示向量的范数,即向量的长度
C:二次成本函数(mean squared error or MSE)
如果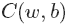
此成本函数中,w和b为变量。
注:hidden layers和output layer中的每个神经元对应一个组w、b。
3.2.1 学习目标
如何找到满足要求的w和b:答案是梯度下降法(Gradient Descent)
1)最小化二次成本函数
2)检测分类的准确性
学习目标:在训练神经网络中,找到使二次成本最小的w和b的集合。
3.2.2 梯度下降更新规则
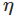
此规则用于在神经网络中学习参数w和b。
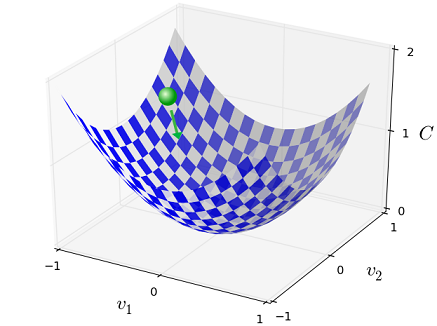
3.2.3 算法推导(梯度下降法: gradient descent)
要求极小值,先讨论具有2个变量的简单情况,然后再推广:
令
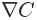
现在的问题是如何选择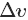
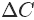
则v的更新规则为:
按此规则,一步一步跌代,C值不断减少,直到全局最小值。
总之,梯度下降法是:重复计算梯度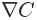
上面讨论了只有两个变量的情况,现在推广到m个变量的情况,对应公式如下:
3.2.4 随机梯度下降法(Stochastic Gradient Descent)
为不减少计算量,把n个学习样本分成很多组,每组有m个学习样本,每次只计算一个组,则有如下推导:
则w和b的更新规则为:
注:如果m=1,则为在线学习(online)。
3.2.5 w和b的数量
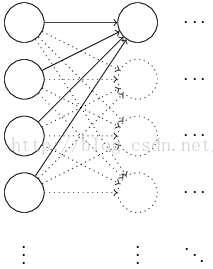
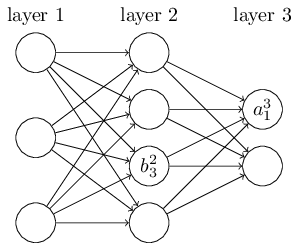
对于hidden layers和输出层的神经元,每个神经元对应一个w向量和一个b,w向量的维数是其输入神经元的数量。第一层神经元没有w和b,其值直接输出。
第一层就表示原始图像数据,这些数据不经任何处理,直接作为Xj参与第二层的运算,第二层首先基于每个Xj,计算其z(z=wx+b),然后计算出sigmoid(z),以此类推。直到最后一层,利用BP算法,先计算最后一层w和b的梯度,然后以此向前,直到计算出第二层的梯度为止。
4. BP算法(反向传播算法)
BP(Backpropagation Algorithm) :是一个计算成本函数梯度的算法。
需要基于每个训练样本计算每一层的w和b的梯度,从而更新每一层的w和b。
BP的真正目标:是计算每个样本的偏导数: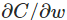
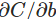
4.1 定义标记符号
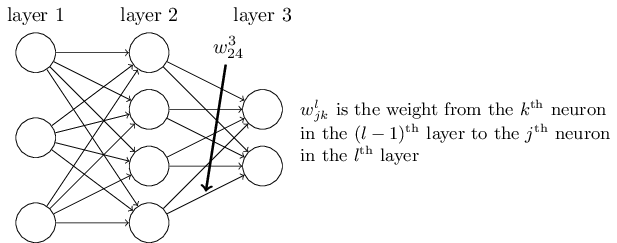
则有激活值的如下公式:
函数向量化有如下形式:
即函数对向量的每个元素分别计算,然后生成对应的向量。
则上面的函数向量表示为:
记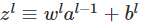
4.2 公式推导过程
4.2.1 计算激活值
4.2.2 最后一层(L层)的二次成本函数
4.2.3 单个训练样本(x)的二次成本函数
4.2.4 定义误差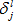
4.2.5 定义输出层误差
4.2.6 求最后一层(L层)激活值的偏导数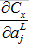
4.2.7 根据最后一层的误差计算前一层的误差
4.2.8 计算目标值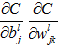
4.2.9 BP的四个基本方程式
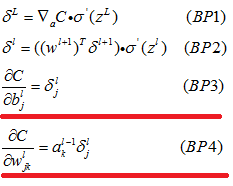
4.3 证明四个基本议程式
4.3.1 证明BP1

4.3.2 证明BP2
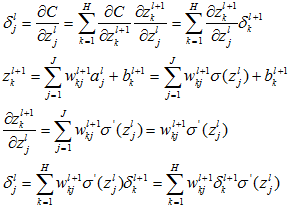
4.4 BP计算过程

5. SGD(随机梯度下降)计算过程

6. 改进神经网络学习方法
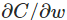 和
和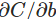 )决定,所以学习速度慢的根本原因是:偏导数太小。
)决定,所以学习速度慢的根本原因是:偏导数太小。
6.1 交叉熵成本函数
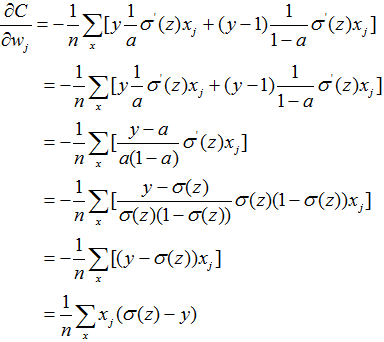
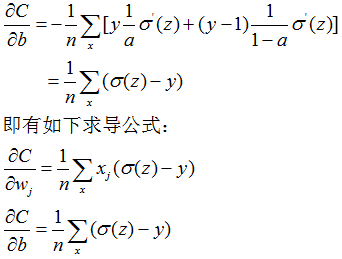
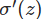 导致的学习速度慢问题。
导致的学习速度慢问题。
6.2 推广交叉成本函数
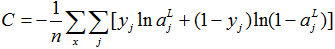
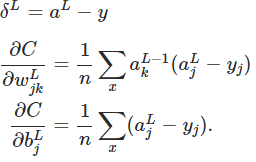
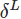 的计算方法,其它计算方法完全相同。
的计算方法,其它计算方法完全相同。
6.3 交叉熵的含义
6.4 Softmax(柔性最大值)


6.4.1 Softmax如何解决学习速度慢的问题?
7. 过拟合和规范化
7.1 过拟合(Overfitting)
7.2 规范化(Regularization)-减少过拟合
规范化(Regularization)也是减少过拟合的方法之一。有时候被称为权重衰减(weight decay)或者L2 规范化。L2 规范化的思想是增加一个额外的项到成本函数中,这个项叫做规范化项。规范化的交叉熵如下:
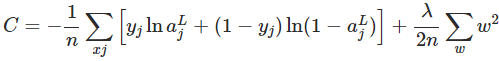
 >0是规范化参数(regularization parameter)
>0是规范化参数(regularization parameter)
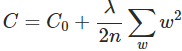
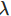 较小,我们期望最小化原始成本函数;如果
较小,我们期望最小化原始成本函数;如果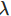 较大,我们期望最小化权重。
较大,我们期望最小化权重。
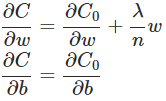
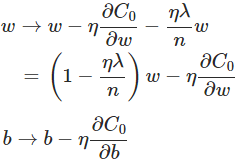
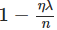
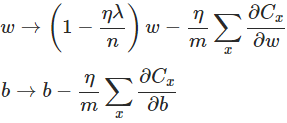
7.3 为什么规范化可以减少过拟合
8. 权重初始化
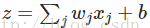
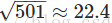 (方差为501)的高斯分布。它是一个非常宽的高斯分布,根本不是非常尖的形状:
(方差为501)的高斯分布。它是一个非常宽的高斯分布,根本不是非常尖的形状:

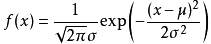
两个都服从正太分布的变量,例如X服从N(a,b),Y服从N(c,d),且X和Y相互独立,则有:
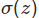 就会接近1或者0,即隐层神经元进入饱和状态了。即隐层神经元的输出
就会接近1或者0,即隐层神经元进入饱和状态了。即隐层神经元的输出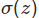 将非常接近于0或1。在这种情况下,权重的修改对隐层神经元的输出激活值影响很小,从而对下一层的隐层神经元、直到对输出层的神经元的输出都很小,从而导致学习速度慢的问题。
将非常接近于0或1。在这种情况下,权重的修改对隐层神经元的输出激活值影响很小,从而对下一层的隐层神经元、直到对输出层的神经元的输出都很小,从而导致学习速度慢的问题。
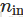 )分布,偏差服从N(0,1)。其中
)分布,偏差服从N(0,1)。其中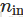 表示此层神经元输入权重个数(即此隐层神经元的输入神经元个数,如上例中
表示此层神经元输入权重个数(即此隐层神经元的输入神经元个数,如上例中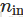 =1000)。权重之后为:
=1000)。权重之后为: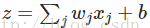 ,其服从N(0,3/2)。
,其服从N(0,3/2)。
9. 神经网络可以计算任何函数
总而言之:包含一个隐层的神经网络可以被用来按照任意给定的精度近似任何连续函数。
10. 为什么训练深度神经网络比较困难?
10.1 消失的梯度问题的根本原因?
11. 卷积神经网络(CNN)
11.1 基本概念
11.1.1 局部感受野
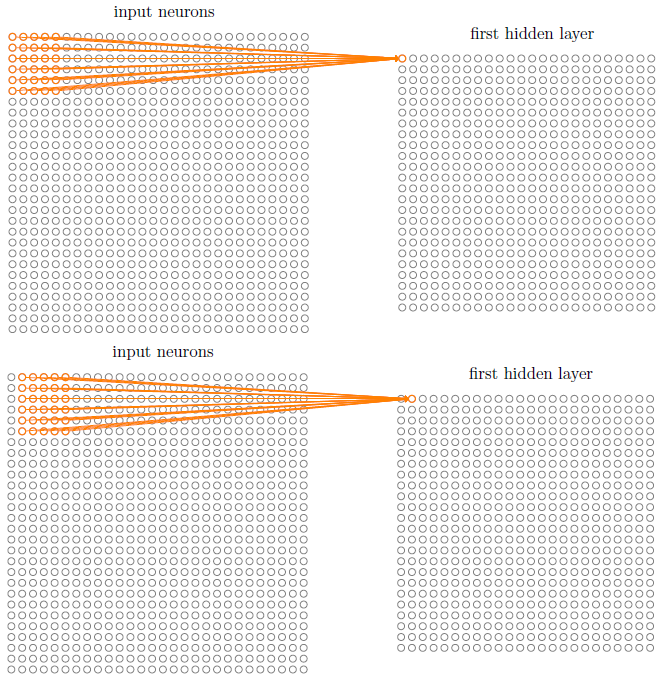
每个连接学习一个权重,且隐层神经元也学习一个总的偏差。即此隐层神经元正在对输入图像的此区域进行学习、了解。一个隐层神经元与一个局部感受野一一对应,即每个隐层神经元有:5x5个权重和1个偏差。
11.1.2 共享权重和偏差
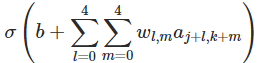
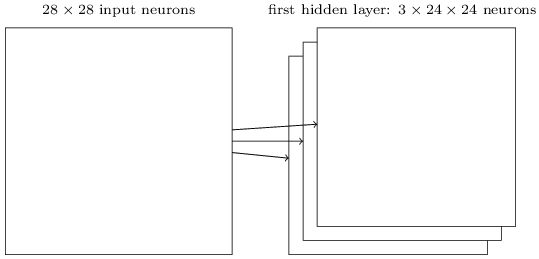

11.1.3 混合层
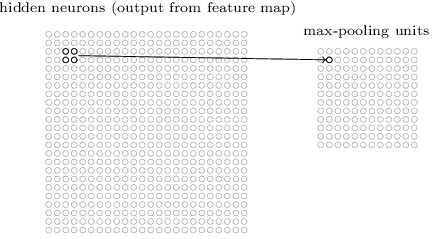
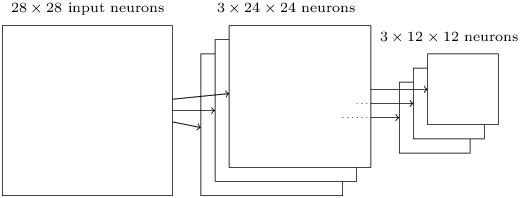
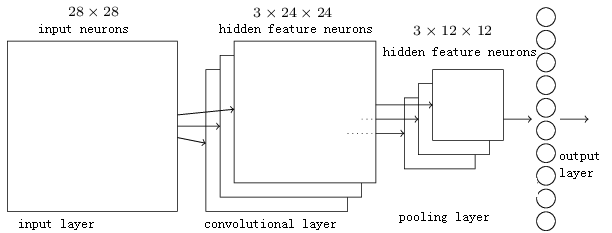
11.1.4 完整的卷积神经网络
更多推荐
 已为社区贡献4条内容
已为社区贡献4条内容
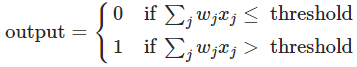

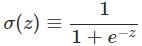

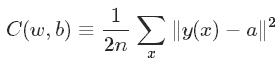
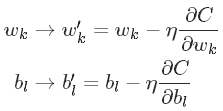
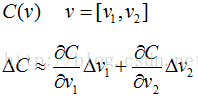
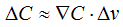
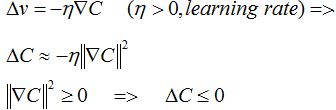
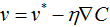
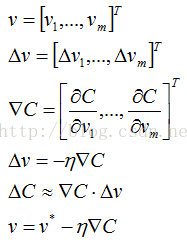
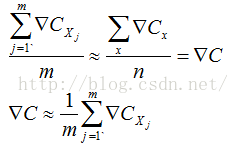
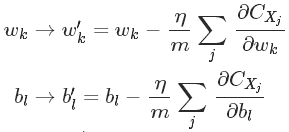
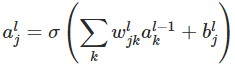
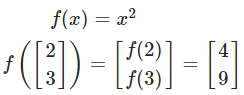
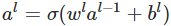
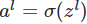

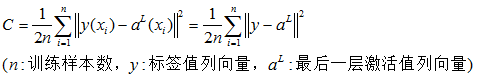


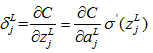


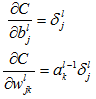








所有评论(0)