一、方差分析的介绍及使用的大致流程

正交实验的方差分析（ANOVA）是一种统计方法，用于分析正交设计实验数据，以确定不同因素和它们的交互作用是否对实验结果产生了显著影响。方差分析通过分解总变异为每个因素造成的变异和随机误差，帮助我们判断实验中各个因素的影响力度。

1.1总变差的分解

这个是参照方差分析中总偏差平方和的分解公式，正交表各列的偏差平方和总偏差平方：

式中，T为数据总和，n为实验总个数，p为列数，比如说L₉(3⁴),那么其中n就为9，p就是4，因素有三水平，则有：

1.2 自由度、方差 、F-检验

1.自由度 ： 各列自由度为该列水平数减1，而总自由度为各列自由度之和，即：

2.方差在第二部分的实例中进行讲解

3.F-检验

F-检验（F-test）是统计学中的一种检验，它用于比较两个总体方差是否相等，或者更常见地，在方差分析（ANOVA）中比较不同组之间的平均数是否存在显著差异。F-检验是基于F分布来进行的，这是一种当两个随机变量的比率是独立的卡方分布变量时产生的概率分布。
这里我们说的是在ANOVA中的F-检验

在ANOVA中，F-检验是用来确定不同处理（自变量或因子水平）对结果变量是否有显著影响。它的基础是比较由于处理效应和随机误差产生的方差。

F-检验的计算步骤通常如下：

1. 计算平均数：

   • 计算每个组的平均数。
   • 计算所有数据的总平均数。

2. 计算平方和（Sum of Squares, SS）：

   • 总平方和（SST）：所有数据点与总平均数的差值的平方和。
   • 组间平方和（SSB）：每个组平均数与总平均数的差值的平方，乘以各组的样本数。
   • 组内平方和（SSE）或误差平方和：各组内部，每个数据点与该组平均数的差值的平方和。

3. 计算自由度（Degrees of Freedom, df）：

   • 总自由度（dfT）：总样本量减去1（N-1）。
   • 组间自由度（dfB）：组数减去1（k-1）。
   • 组内自由度（dfE）：总自由度减去组间自由度（dfT - dfB）。

4. 计算均方（Mean Square, MS）：

   • 组间均方（MSB）：组间平方和除以其对应的自由度（SSB/dfB）。
   • 组内均方（MSE）：误差平方和除以其对应的自由度（SSE/dfE）。

5. 计算F值：

   • F值：组间均方除以组内均方（MSB/MSE）。

6. 查F分布表或使用统计软件：

   • 根据得到的F值和对应的自由度（dfB和dfE），在F分布表中查找或使用统计软件得到p值。

7. 作出结论：

   • 如果计算出的F值大于某个显著性水平（例如，α = 0.05）对应的F分布表中的临界值，或者p值小于显著性水平，我们拒绝零假设，表明组间至少有一组平均数存在显著差异。
   • 如果F值小于临界值或p值大于显著性水平，我们不能拒绝零假设，表明没有充分证据认为组间平均数存在显著差异。

F-检验是一个非常重要的统计工具，特别是在实验设计和假设检验中，它帮助研究人员确定数据中的变异是否可能是由于实验中的因素而非偶然误差所引起。

二、实例说明

以下面这个表格中的数据为例进行说明，其中有A B C D E 五个因素，两个水平

按照上述偏差平方和，可以计算得到，

这里以第一列为例进行计算说明，
通俗点讲公式为：（不同水平数据和的平方相加）/水平数-一整列数据和的平方/行数
按照公式（339.5²+358²）/2-(339.5+358)²/8=42.78
其余的按照此算法计算；
由于Q₃<Q_B<Q_A,
我们暂且认为A、B间没有交互作用，第三列是误差列，但是Q₃>Q_D,因此D因素无影响
我们把误差项加起来得到：
Q₃+Q_D+Q₇=1.003
其自由度为：f₃+f₇+f_D=3
接下来进行F-检验，一般可考虑四种情况：
1.F>F_0.01(f_因,f_e)，则因素对结果的影响高度显著，记为：***或者 **
2.F_0.01(f_因,f_e)>=F>F_0.05(f_因,f_e),则该因素对结果有 显著影响
3.F_0.05(f_因,f_e)>F>F_0.10(f_因,f_e),则该因素对结果有影响
4.F<=F_0.10(f_因,f_e)
顺带在这里讲一下方差分析方法：
1.单因素方差分析
单因素就是只有一种因素多个水平，用下表进行分析

2.无重复两因素方差分析
无重复两因素方差分析（Two-way ANOVA without replication）用于研究两个不同独立变量（因素）对一个连续型因变量的影响，且每个因素水平组合的实验只进行一次。这种分析方法允许研究者评估两个因素以及它们可能的交互作用是如何影响结果的。
a是因素A的水平数，b是因素B的水平数

可以看出，随着因素增多计算越麻烦，通常会使用统计软件（如R、SPSS、SAS）来执行这些计算，因为手动计算可能会非常繁琐并且容易出错，这里面采用SPSS软件进行计算，说明，因为手动计算实在麻烦；
SPSS的资源好找，安装也不难，就不详细展开了，下面讲述一下用spss操作的步骤：

在数据编辑器中设置如下：

这几个名称对应的是实验中的ABCDE，指标就是每组实验的结果，然后按照实验表里面的填入数据，注意正交表里的交互作用和误差列就别填了，咱们这里只是简单的案例：

然后找到分析-一般线性模型-单变量，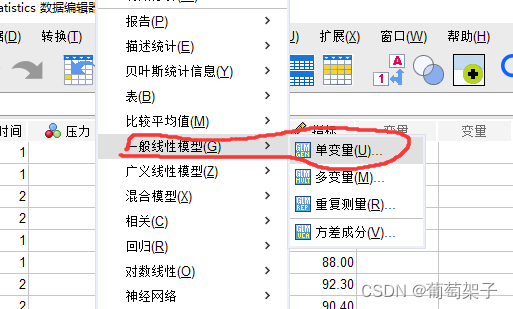

接下来，把指标放到因变量里面，其他放入固定因子里面

接下来是模型选项，按照这个，不能看全因子了，因为因素太多，数据太少：

然后在选项里面点击齐性检验：

点击继续后，点击确定，然后出来数据：

模型显著性为0.035，说明数据显示模型中的变量与响应变量之间存在统计上显著的关系，这意味着实验数据在统计学上是有效的。