PS: 本文为台大机器人学学习笔记，也转载了其他博主的一些内容。原B站视频链接如下：台大机器人学之动力学——林沛群_哔哩哔哩_bilibili

一.微分运动学与雅克比矩阵

1.位置向量的微分描述该点的速度

2.角速度向量的表达

3.Rigid Body Motion：

A点对地的速度=B点对地的速度+A点由小坐标系看的速度+ w 和 a 对b向量的叉积

 对应到机器人学中，速度在不同坐标系下的表达以及关系式：

4.速度传递 Velocity “Propagation”

（1）旋转关节Rotational Joint

角速度传递Angular velocity propagation：

从 i 来看的 i+1 的角速度 = 从 i 来看的 i 自己的角速度 + link(i+1) 的旋转所造成的效应。

在 {i+1} 上来看 link(i+1) 的角速度就是上述等式左右同时乘以 i 对 i+1 的旋转矩阵。

线速度传递Linear velocity propagation ：

从 i 来看 i+1 的速度 = 角速度与旋转半径的叉积 + 从 i 来看 i 的速度。

 （2）移动关节Prismatic joint

5. Jacobians

接下来探讨是不是可逆的问题，上面讨论的是由关节空间推出笛卡尔空间，那么如果已知的是笛卡尔空间想知道关节空间呢？雅克比矩阵可逆吗？如果雅克比矩阵的行列式为零的话，就找不到他的逆矩阵，这种状况叫做 singular ，什么状况下会造成它 singular 呢？

6.Example

 方法一：速度传播法

 

求出雅克比矩阵（3*2），求行列式的值，当θ2等于0°或者180°的时候行列式的值为零，此时是处于 singular 的状态。 

方法二：直接微分法

二.力传递

上面我们在位移分析的基础之上进行了速度分析，雅克比矩阵揭示了机器人操作空间速度和关节空间速度之间的线性映射关系，不仅如此，雅克比矩阵也可以用来表示两空间之间力的传递关系。

将机器人系统定格在某一刻，探讨机器人各关节处的力和末端执行器处的力有什么关系？

 1.Example

假设手臂末端单纯受到一个力，没有力矩。要从 {3} 中看到的 f3，推导出 {2} 中看到的 f2，需要做一个旋转转换，3对2的旋转变换又是单位矩阵，这说明末端点收到的力会原封不动的反应在前面的关节上面。

可以发现，力传递的雅克比矩阵和之前速度传递的雅克比矩阵只差一个转置。

（末端执行器）力 * 微小位移 = （关节）力矩 * 角位移

一旦我们知道由关节空间的关节角速度得到末端执行器速度的雅克比矩阵，我们就可以利用该雅克比矩阵的转置找到末端执行器对地的力和关节力矩之间的关系，而不需要重新做复杂的 IK。

三. Newton’s Equation and Euler’s Equation

1. 定义线加速度

和之前一样，速度是位置的微分。在这里，加速度是速度的微分：

把得到的加速度表达在另一个坐标系下面

2. 定义角加速度 

线速度线加速度有这样的关系之外，角速度角加速度也有这样的对应关系，角速度的微分就是角加速度。

3.线加速度 

由前面所学，知道A点对地的速度 = B点对地的速度 + 由B点看到A点的速度 + B所在坐标系在旋转过程中造成的向量 r(a对b) 的变化。

合并项之后，整理得

 A点的加速度 = B点的加速度 + B相对于A看不到的部分，切向加速度（角加速度与r的叉积） + 法向加速度 + 人站在B坐标上看到的相对加速度 + 科式力。

4. 角加速度

{C} 对 {A} 的角速度 = {B} 对 {A} 的角速度 + {C} 对 {B} 的角速度（又因为在相加计算的过程中要转到同一个 frame 下，所以 {C} 对 {B} 的角速度前还要乘上一个旋转矩阵）

对这个式子作微分，这里 {C} 对 {B} 的部分有两个项，遵循前导乘后 + 前乘后导的原则，那对旋转矩阵求导是什么呢？

依照之前的想法，我们知道旋转矩阵是由三个单位向量所组成的，这三个单位向量互相正交，对旋转矩阵求导，相当于对三个单位向量求导，之前学过，对单位向量求导，它的长度不会变化，变化的只是它的方向。由于这里是旋转矩阵，所以单位向量的变化基本取决于整个坐标系旋转的状态，因此，{B} 对 {A} 的旋转矩阵的倒数 = {B} 对 {A} 的角速度与旋转矩阵本身的叉积。（如红框部分所示）

5. 质量分布(Mass Distribution)

相对于 frame {A} 的惯性张量

惯性张量本身的特性：

• 是常实对称矩阵，在数学上是可正交对角化的
  

• 对角线元素之和为定值
  

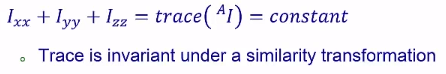
• 如果刚体的本身存在某个对称面，这个对阵面上下的值就会是零
  
  在算惯性矩阵的时候，必须要有转轴
  平行轴定理：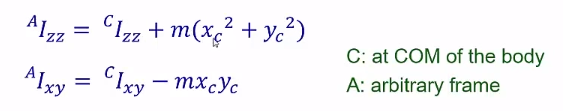
  
  

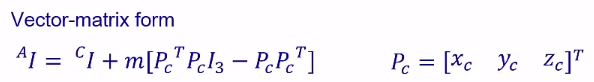
6. 牛顿-欧拉递推动力学方程 

【大学物理知识回顾】
转动惯量 J 由刚体的各个质元相对于固定转轴的分布决定，与物体的运动以及所受的外力无关，是用于描述刚体相对于确定转轴特征的物理量。
动量 P=mv ，动量的变化量是合外力；
角动量L=Jw ，角动量的变化量是定轴转动刚体所受的力矩

杆件有加速度，必须受到惯性力F，杆件要转动，必须要受到扭矩N；

• 针对移动的部分，牛顿运动方程；
  线动量的变化量等于外力，牛顿第二运动定律；
• 针对转动的部分，欧拉方程；
  角动量的变化量等于力矩；

这里要特别小心 I 定义的 frame，因为在不同的 frame 下面，I 的定义会不一样；和之前相反，我们不希望 I 定义在地坐标系下面，杆件在空间中是运动的，地坐标系不动，就等于说这个杆件以地坐标系来看的话，它和地坐标系之间的相对距离一直变动，所以它的 I 以地坐标来看的话就一直变动，这样取倒数的时候就需要考虑 I的倒数，会使欧拉方程的求解变的复杂。

通常情况下我们会在质心的位置定义坐标系，由于这个坐标系与这个杆件固连，所以 I 不变。推导后的力矩由两项组成，第一项就是杆件的角加速度造成的，注意这里的 I 是对于建立在质心处的坐标系而言的，还有一部分就是由于系统的角速度造成的。

（1）旋转关节Rotational Joint

角加速度传递Angular acceleration propagation：

线加速度传递Linear acceleration propagation ：

i+1 杆件的线加速度 = i 杆件的线加速度 + 切向加速度 + 法向加速度（还应该有两项科式力和相对的加速度，要是仔细看的话会发现，该式子是为了找到 {i+1}杆件 frame 的原点相对于 {i}杆件 frame 原点的加速度，而{i+1} 旋转时并不改变原点的位置，所以后边两项就没有了）

  （2）移动关节Prismatic joint

角加速度传递Angular acceleration propagation与线加速度传递Linear acceleration propagation：

连杆质心的线加速度：除了上述的坐标原点的状态，连杆质心（COM）的状态也会用到，因为算惯性力的时候，就必须要算这个link 的COM的加速度是多少，我们才有办法借由这个加速度乘上质量m得到这个杆件受到的外力是多少（COM点在连杆的中部）

在找到了杆件和杆件之间加速度的关系后，现在要怎么跟力矩做一个连接？前面通过外推法计算出每个连杆质心的线加速度和角加速度后，运用牛顿-欧拉公式便可计算出作用在连杆质心上的惯性力和力矩：

假设 link(i) 有一个运动，那么基本上杆件所受的合力就等于运动的加速度乘上它的质量；
假设这个杆件有一个角加速度和角速度，假设也知道这个惯性张量对COM来看是已知的话，所受的外力矩就等于上述式子。

（3）计算力和力矩

上面计算出每个连杆上的力和力矩后，我们就要计算出产生这些力和力矩的需要施加在关节上的关节力矩。

有了这个想法之后就可以分别来看力和力矩的状态。
以力的状态来说，力是由末端点往回算的（手臂末端点受到力，后面有力就代表前面关节都要承受住这个力，这个是和速度相反，速度是地的 link 不动，随着 link 往前增加，后面的 link 都要承载前面 link 的运动，然后再产生一个新的相对继续往后算）

将作用在连杆i ii上所有的力相加，得到力平衡方程：
frame {i} 所需要的力 = {i+1} 这个 frame 的力 + 让 {i} 本身产生运动所需要的惯性力

将所有作用在质心上的力矩相加，得到力矩平衡方程：
力矩是建立在相似的概念上的，力矩这里会有点复杂，在于杆件原本受到的力也会产生力矩，所以力矩所包含的项就会比较多。
i 杆件所要承受的力矩 = i+1 所要承受的力矩（i+1之后的杆件传到 i+1 的力矩） + 让 i 产生转动所需的惯性力矩 + 惯性力 Fi 所产生的力矩 + i+1 杆件的外力所产生的力矩

那么怎么求得关节力矩呢？
在静力学中，可以通过计算一个连杆施加于相邻连杆的力矩在Z方向上分量求得：

关节类型不同，计算马达负载的方式也会不同。针对旋转关节，会用力矩对 Z 轴做投影；针对移动关节，用力对 Z 轴做投影。让我们真正算出来在真正在动力学考量下面，我们的系统在完成运动时所需要的各个 joint 的力矩是什么。

我们现在有了运动的状态，有了速度和加速度的公式，也有了力和力矩的公式，那也就是真正面对一个问题的时候，先把运动状态算完，运动状态是由地杆往上算，算到末端执行器之后，就可以获取整个手臂的速度和加速度状态。
有了这个之后再导入所谓的力，假设末端点会有某个力，再往回算，获取力和力矩。
上行是计算速度和加速度，下行是计算力和力矩，都计算完之后，我们才能由力和力矩去投影计算 每一个joint 所需要的出的力是多少。

7.Example
 

假设第一、二个杆件的质量分别集中在各自的末端点，相当于质点，有两个质量 m，但是没有惯性矩阵 I；
假设手臂末端点没有受力，所以 f3 = 0，n3 = 0；
考虑重力场，则地杆有一个向上的加速度（即沿着Y0方向的大小为 g 的加速度），等效过来就是一个向下的重力。由于地杆不动，所以角速度、角加速度为零。
由于都是旋转关节，旋转矩阵都是标准的绕着 z 轴旋转的公式。

                      

速度与加速度传递：

• 第一轴的角速度 = 第零轴的角速度 + Link 1 本身旋转造成的角速度，地杆不动，所以第一项为零。
• 根据之前学习的公式求解角加速度，第零杆没有角加速度，也没有角速度，所以前两项为零。
• 求解第一杆件的线加速度
• 求解第一杆件的质心的线加速度

• 第一杆件的惯性力 = 第一杆件质心线加速度 * 第一杆件的质量
• 计算第一杆件的惯性力矩，由于杆件本身没有转动惯量，所以结果为零
• 计算角加速度，由于第一杆件的角速度方向和 θ2(dot) 方向相同，所以第二项叉积结果为零

• 有了 frame{2} 的状态时候，再来计算第二杆件质心的线加速度，此时相当于拉到了第二杆件末端点的位置。

 力和扭矩传递Force and torque propagations

 关节扭矩：

公式中可以看到手臂的 τ 有很多项组成，现在要对其进行拆解，让我们可以看出来 τ 受到哪些项的影响。

（1）拆解方式一：The state-space equation 

分解成三个群组，第一个是惯性群组，这里考虑到惯性力的部分；第二个群组包括一些剩下的一些力，包含离心力科式力（同时是角度和角速度的函数）等；第三部分就是重力，跟位能有关，几何有关，所以是 θ 的函数。

按照上述方式拆解后，三个矩阵分别长这样：

M（θ）是2*2的矩阵，从这里可以看出，越前面的杆件，它所需要承载的力道就越大。
G（θ），τ 2 只需要负担第二个杆件的重力。

（2）拆解方式二：The Structure of Dynamic Equations 

这个方法相比之前的就是将 V（θ，θ（dot））拆解的彻底一些。科式力是交错的，因为他是在相对的坐标系下有相对的运动，如果一个机械臂有 n 个自由度，那么科式力项就应该是 C n 取 2，即 θ1(dot)到θn(dot)之间的排列组合。
针对一个 n 自由度的手臂，离心力就有 n 个分法。

所以按照上述方法，再把刚刚的V（θ，θ(dot)）项拆解一下。

四.拉格朗日方程Lagrangian Formulation 

 1.定义

之前我们学习了如何使用牛顿-欧拉法（基于力和力矩分析）建立机械臂的动力学方程，这一节要学习拉格朗日法（基于能量分析）建立机械臂的动力学方程。

动能
每一个杆件的动能 = 移动动能 + 转动动能
整个系统动能 = 所有杆件动能之和
动能是角度和角速度的函数，写成通用矩阵式。

势能
每个杆件的势能 = 每个杆件的重力势能 + 零势能点
整个系统势能 = 所有杆件势能之和
势能是角度的函数 。

Lagrangian 表达式：

2.Example ：An RP Manipulator

3. 转换到笛卡尔空间下

我们写出来的动力学方程是 joint space 下的方程式，也就是我们知道了每个手臂关节的状态就可以知道达成这个运动状态所需要的关节的扭力是多少。

在笛卡尔空间下面，在看末端点的加速度状态的时候，末端点的加速度和力的关系是什么？那现在就可以使用之前学习过的雅克比矩阵把本来的方程式转换到笛卡尔空间下面的运动方程式。

 

重新回看之前双旋转自由度机械臂的例子，之前是用牛顿-欧拉法去做，并且找到了以下三个矩阵 ：

我们现在想做的事是把它换到笛卡尔空间下面，在微分运动学中我们已经得到了雅克比矩阵 J(θ) ，所以它的逆矩阵和导数，之后就是代公式：

像之前一样将科式力和离心力也拆解出来，拆解的更彻底一点。 

 注意：我们在推导拉格朗日方程的时候认为力做的功都转换为了动能和势能，过程中没有损耗。但是在实际机械臂中，没有摩擦是不可能的。这里引入阻尼力损耗的概念，那另外一个就是库仑摩擦，基本上是一个定值，但是它在静止时和运动时是不一样的，分为静摩擦和动摩擦