本文详细的解答了TI杯2023年全国大学生电子设计竞赛综合测评的所有要求，包括方案设计，multisim仿真详细每一步调试过程，及实际焊接结果等。非常详细。希望对您有帮助。

题目： 求解线性常微分方程的模拟计算机（23年电赛综合测评）                                         

概括来说，题目要求即为：

√以两片LM324DR四运放放大器芯片作为基础，完成以下内容：

1. 产生角频率为600rad/s的正弦波，并且波形幅度大于2V（即VPP>4V）（初相位不限）
2. 产生与正弦波同频同相的三角波，并且波形幅度大于2V
3. 构建模拟计算机系统，在初始条件：

的条件下，分别完成以下三种输入信号时对微分方程的解：

微分方程为：

输入信号分别为：

①0（即不输入，输入端接地，对应齐次解）

②600rad/s的正弦波(幅度大于2V,初相位不限)（对应非齐次解）

③与正弦波同频同相的三角波（幅度大于2V）（对应非齐次解）

注：输入信号中②③即为题目第（1）（2）问产生的波形。

更进一步来说，就是用lm324芯片产生题目要求的正弦波和三角波，作为激励进入设计好的模拟计算机，用示波器观测模拟计算机输出波形，即方程的非齐次解。外加输入为0时所得到的齐次解构成通解。

一.原理分析

我的总体方案图

1.模拟计算机输入信号产生部分

题目要求产生一路角频率=  600rad/s

(即频率大约为95.5hz)，并且VPP>4V的正弦波信号，和一路与正弦波同频同相的三角波信号。

我采用的方案是先用运放设计一个方波产生电路，再经过反向积分器产生所需要的三角波，再将三角波输入低通滤波电路，滤除得到三角波基波频率分量，即与三角波同频的正弦波，此时由于所产生的三角波与正弦波相位不相同，因此后级接一级移相电路对正弦波进行移相，使得三角波与正弦波同相。

下面，将对各部分电路原理进行分析：

（1）方波产生电路

（2）三角波产生电路

Rf的作用是限制积分器的低频增益，以抑制漂移的影响，Rf尽量取大一点，这样才能避免Rf的引入影响积分特性。在低频时，由于电容C认为是断路，因此上图不再是积分器。其作为积分器使用的下限截止频率是

（3）低通滤波器产生正弦波部分

        三角波为周期信号，周期信号进行傅里叶变换就会得到基波和各次谐波，将其通过一个三阶的有源低通滤波电路，低通电路上限截止频率设置在三角波基波频率的1.5倍左右，就可以很好的滤除其各次谐波，从而保留三角波的基波正弦分量。

（4）移相电路

        将正弦波的输出端接入移相器，示波器上同时显示三角波和正弦波，通过移相器，调节R1，改变相位，使三角波和正弦波同频同相。该电路使电路相位后移，具体角度分析计算如下:

        选择C=1uf，可使95.5Hz的正弦波调正相位明显，并且将R换作滑动变阻器，实现一定的放大，达到性能指标Vpp>4V。

2.模拟计算机设计部分

（1）通用模拟计算机原理分析：

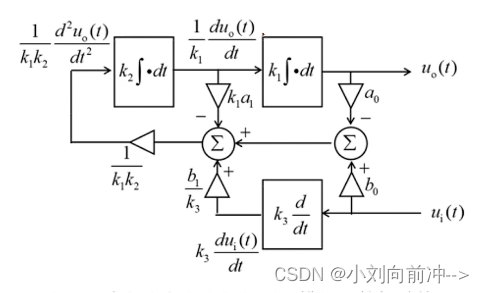
图 2-1二阶微分方程求解的通用模拟计算机结构-1

对于实二阶常微分方程：

，解此方程的通用模拟计算机结构如图2-1所示。将以上方程对应图2-1的结构，在第二个加法器处，将方程进行转化为：（2-1）

通过题目已知：（2-2）。

将方程（2-1）和方程（2-2）进行对比得到:

因此，图2-1的结构中，通过第一次积分进入第二次加法器的部分和进入微分电路，以及

的增益或衰减的放大器，等效于没有。通过分析，简化框图如下：

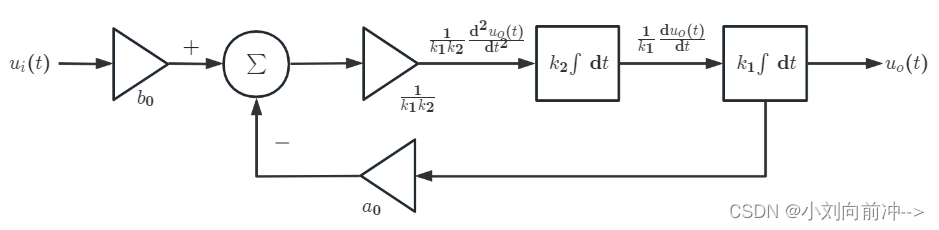图 2-2 简化框图通用模拟计算机结构

其中，k1,k2分别是两积分器的积分常数，k3为微分器的微分常数。

将（2-2）方程，进行变形，

得出：，假设,,得出

（2-3）

由图2-1的结构，得知，因此，积分器的R和C，我们可以从中得知是：,,取，计算较为方便。设,,通过总体分析，只需要三个运放即可完成图2-1的模拟计算机框图，信号经过加法器以及两次积分器，即可。

（2）微分方程的通用计算机设计：

①根据题目已知，时，,;对应齐次解，即实现零输入时，模拟计算机能产生31.83Hz的余弦波。

        分析图2-2可知，求和和两个积分电路形成一个闭环，而闭环之外输入信号,，所以要想获得零输入相应，就应该是此系统自激震荡产生，一个闭环系统必须满足巴克豪森稳定性准则：

巴克豪森稳定性准则德国物理学家巴克豪森于1921年提出的准则。 具体内容概括为：

电子振荡器系统振荡的必要条件：

*电子振荡器系统信号由输入到输出再反馈到输入的相差为360°

*电子振荡器系统信号由输入到输出再反馈到输入的增益为1

（增益大于1起振，增益等于1则稳定）

        理论上来说，每经过一级积分器可以产生90°的相移，电路中经过两级积分器应该是相移180°，再加上电路中的反向比例电路对波形反向（即相当于相移180°），则环路电路总相移加起来为360°，满足巴克豪森稳定性准则。但实际电路中，积分器会受到影响从而产生的不是精准的90°的相移，因此电路中需要再加一级移相电路进行补偿，使得整个环路相移达到360°，再调节反向比例电路使环路增益大于一从而起振得到方程齐次解。电路框图如下:

②根据题目已知

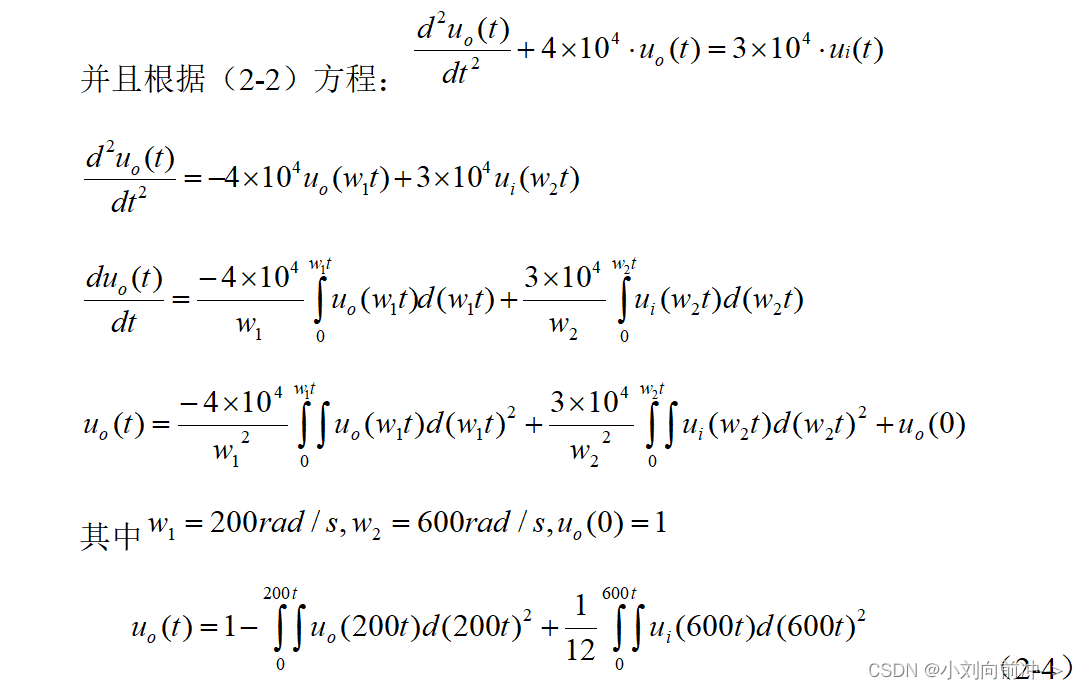        从方程（2-4）中分析得出，输入的波形为95.5Hz的正弦波或三角波，并且频率为95.5Hz的正弦波需要经过两次积分，输出的波形为31.83Hz的波形，同时也需要经过两次积分，当零输入的时，电路会自激振荡出31.83Hz的波形，是零输入响应的状态，同时是整个电路的初始条件。

结合以上的分析，设计电路图如下：

二.仿真内容

（一）总体电路连接

(二)matlab模拟计算机解微分方程仿真结果分析（用于对照multisim仿真，验证multisim仿真结果是否正确）

matlab搭建模拟计算机

观察输出结果

        matlab搭建模拟计算机显示三种输入信号下产生的相应都为31.8hz，并且0输入时产生一个正弦波，正弦波输入时产生马鞍波，三角波输入时产生类正弦。

（三）各部分电路仿真测试

1.输入信号产生部分

（1）方波产生电路

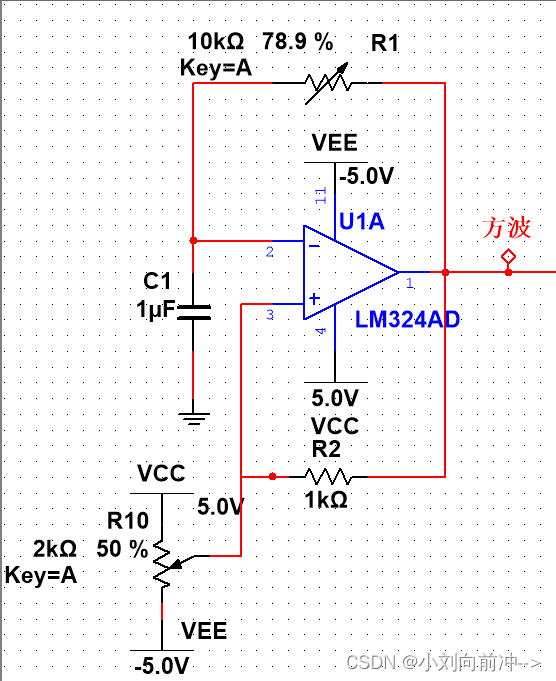
        搭建电路后输出接示波器点击运行，等待方波起振，起振后由于324芯片输出摆幅不对称导致输出不是占空比50%，调节R10使得占空比回到50%，之后调节电位器R1使得输出频率达到95.5hz。

输出端探针显示方波频率为95.5hz，输出VPP为9.14V，示波器显示波形为方波。

（2）积分电路（三角波）

        将方波接入积分电路，示波器观测，R4电阻拉满防漂移，调节R5使电路达到合适积分参考点，调节R7改变三角波斜率以满足幅度要求。

得到标准无失真三角波，频率95.5hz，VPP为5.5V满足>4V要求

（3）低通滤波电路（正弦波）

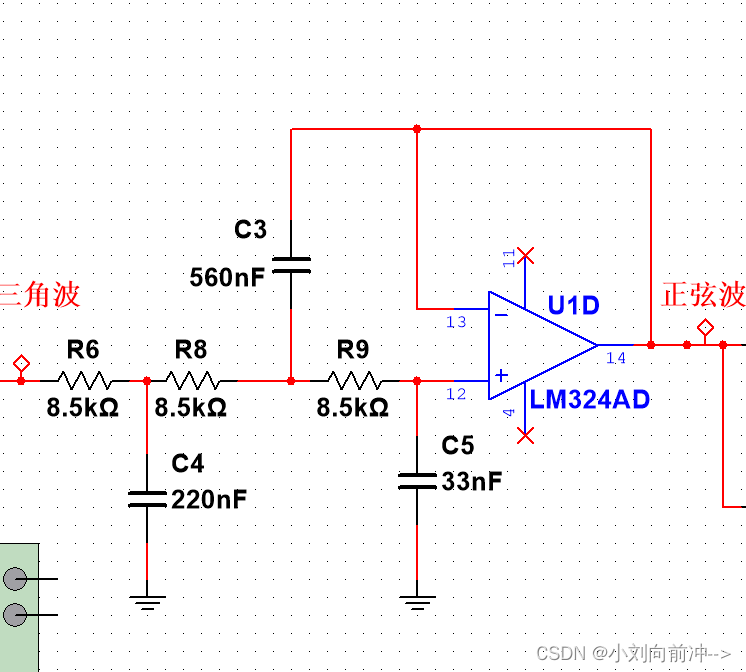
将三角波接入低通滤波电路，示波器观测输出波形。

观察发现波形完美无失真，频率正确，VPP为4.18V，满足要求。

之后将三角波和正弦波接入同一示波器两个通道进行观测，检查两者波形相位是否满足同相位。

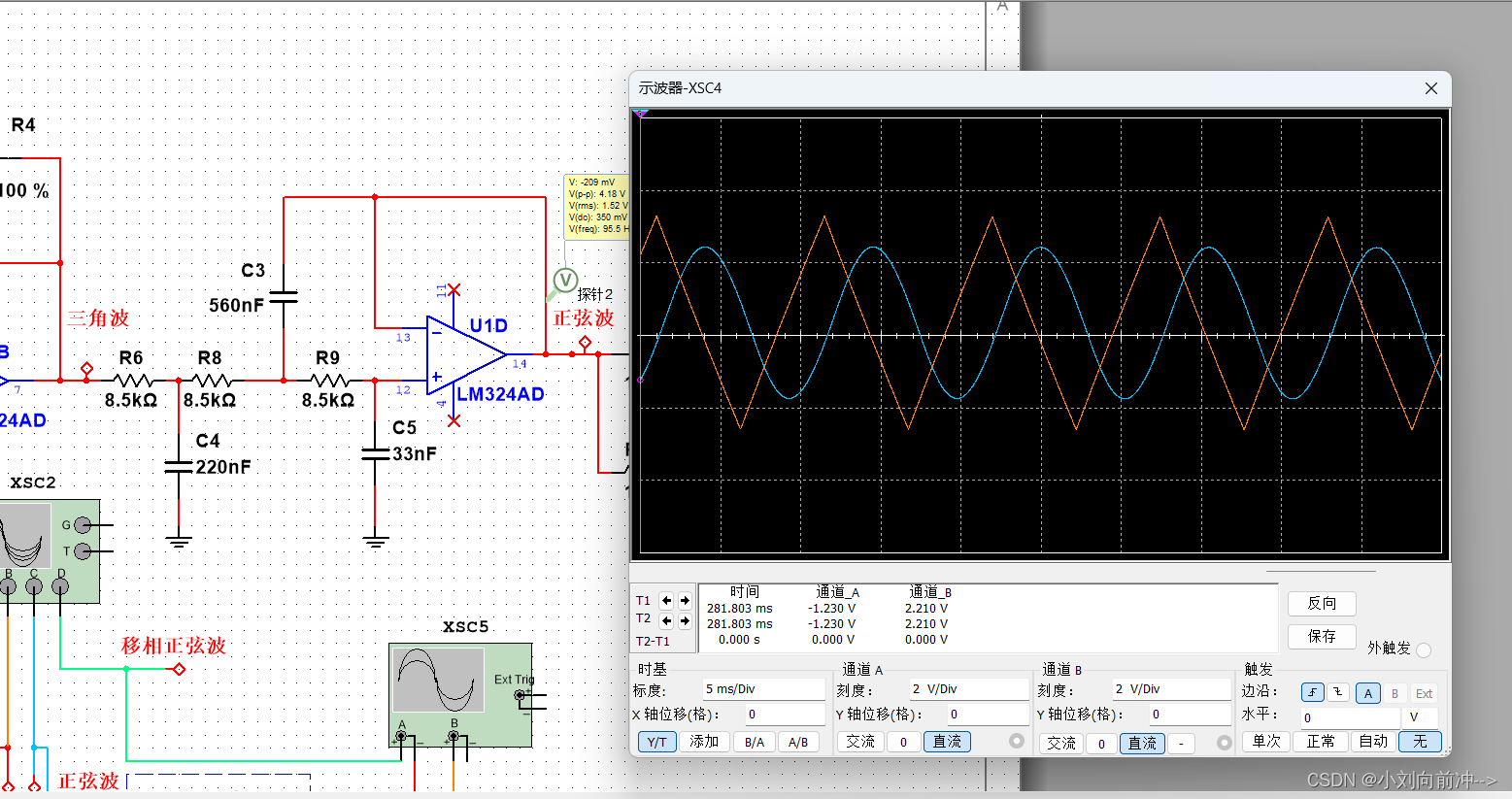从示波器观测看到两者相位并不相同，因此后接移相电路进行调整。

（4）移相电路

将三角波和移相正弦波接入示波器的两个通道，调整R3电阻使正弦波与三角波同相位。

可以看到，移相后三角波与正弦波实现同相位。

2.模拟计算机部分

（1）首先根据先前理论分析搭建齐次解（输入为0）时的部分，此时收入为0，构成环路，环路需要满足巴克豪森稳定性准则才能震荡。下面是我的调试过程：先搭建出反相比例和两个积分器电路，用函数发生器发生一个31.8hz的正弦波接入积分器，用示波器观测输入信号与反相比例电路输出信号两者波形的相位关系，是否满足巴克豪森准则（即两者相位相差360度）

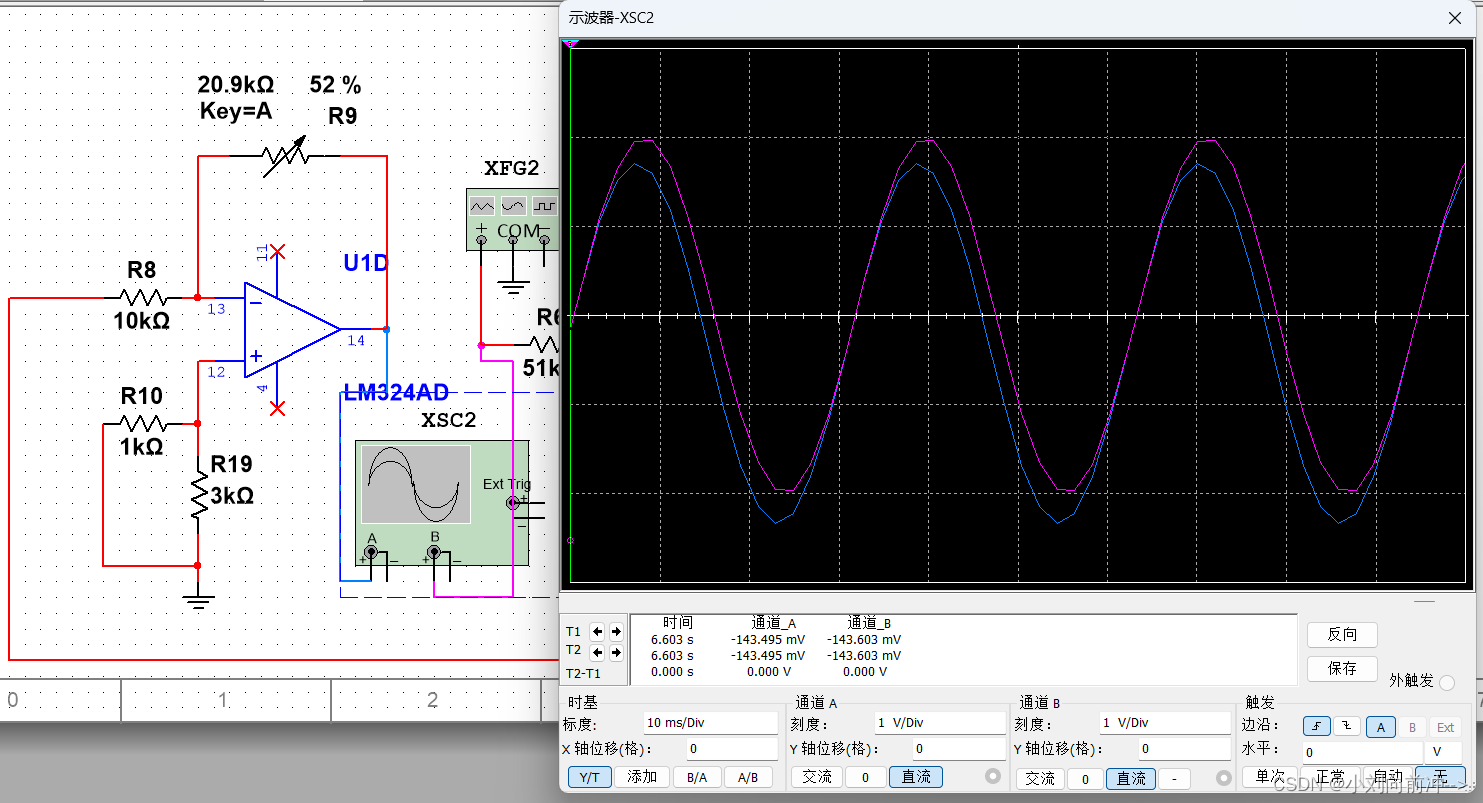        此时可以看出两波形是不满足相位差为360度的，也就是说系统不满足巴克豪森准则，因此电路还应该加一级移相电路调整。

如图所示，电路加一级移相电路，调整移相电路移相值，使得两波形满足相位差为360度。

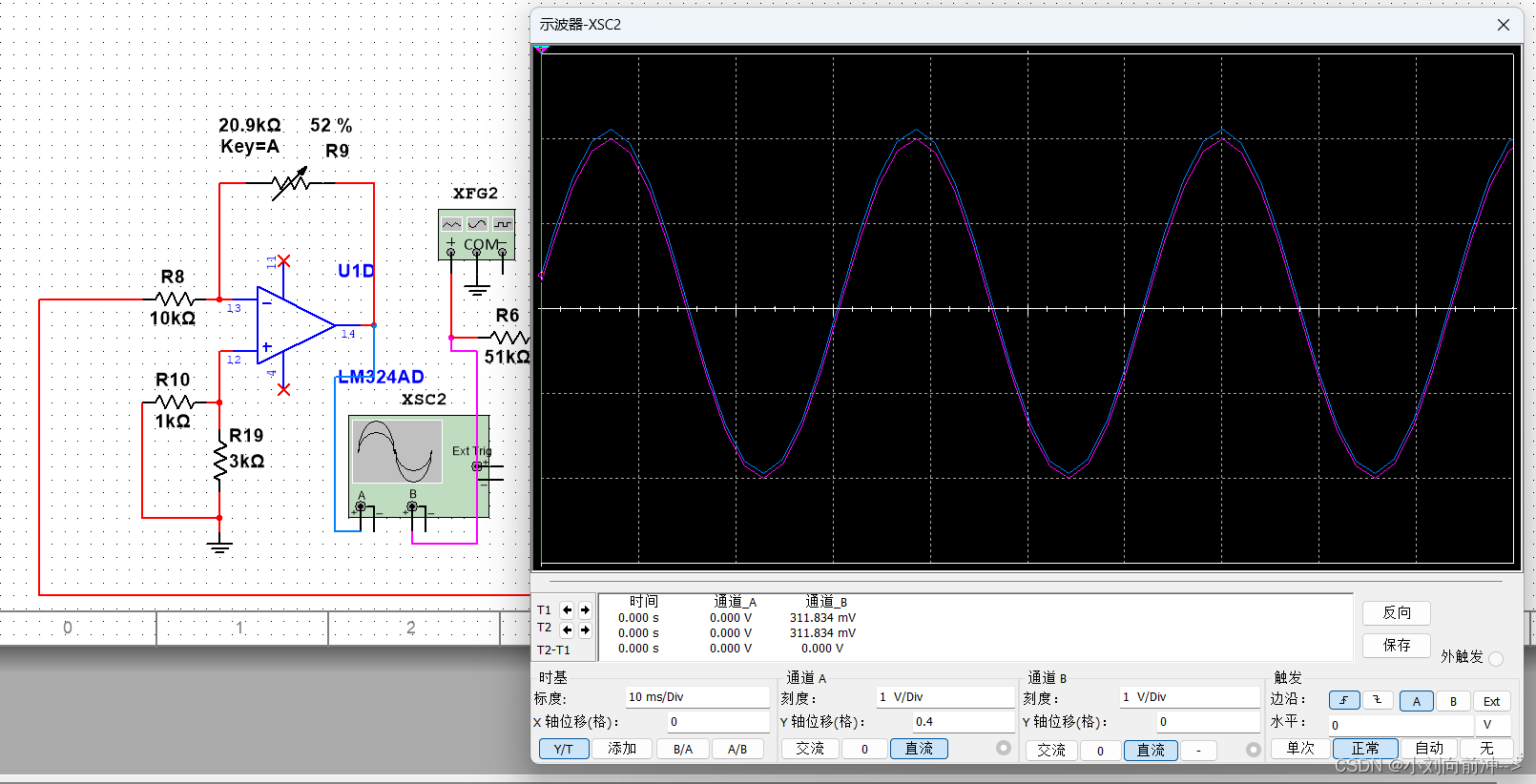
经过移相器处理后发现两波形满足相位差为360度，满足巴克豪森准则的相位条件。

下面调试巴克豪森准则的起振条件：

        在积分电路输入端和反相比例输出端分别放一个探针，运行后观察探针上VPP的数值，通过调整R18电阻改变环路增益，当两个探针的VPP显示值一样时认为环路增益恰好为1，记录此时滑动变阻器R18的数值，此数值对应环路增益为1

之后将函数发生器移除，并将积分电路输入端和反相比例电路输出端相连构成完整回路。

        点击运行，并调整反相比例电路的R18电阻值，使得环路增益大于一，使环路起振。并用示波器观测。

可以看到环路在缓慢起振。

        电路起振之后调整滑动变阻器R18的数值，使之回到之前记录的使系统增益为1时候的数值，使电路稳定。

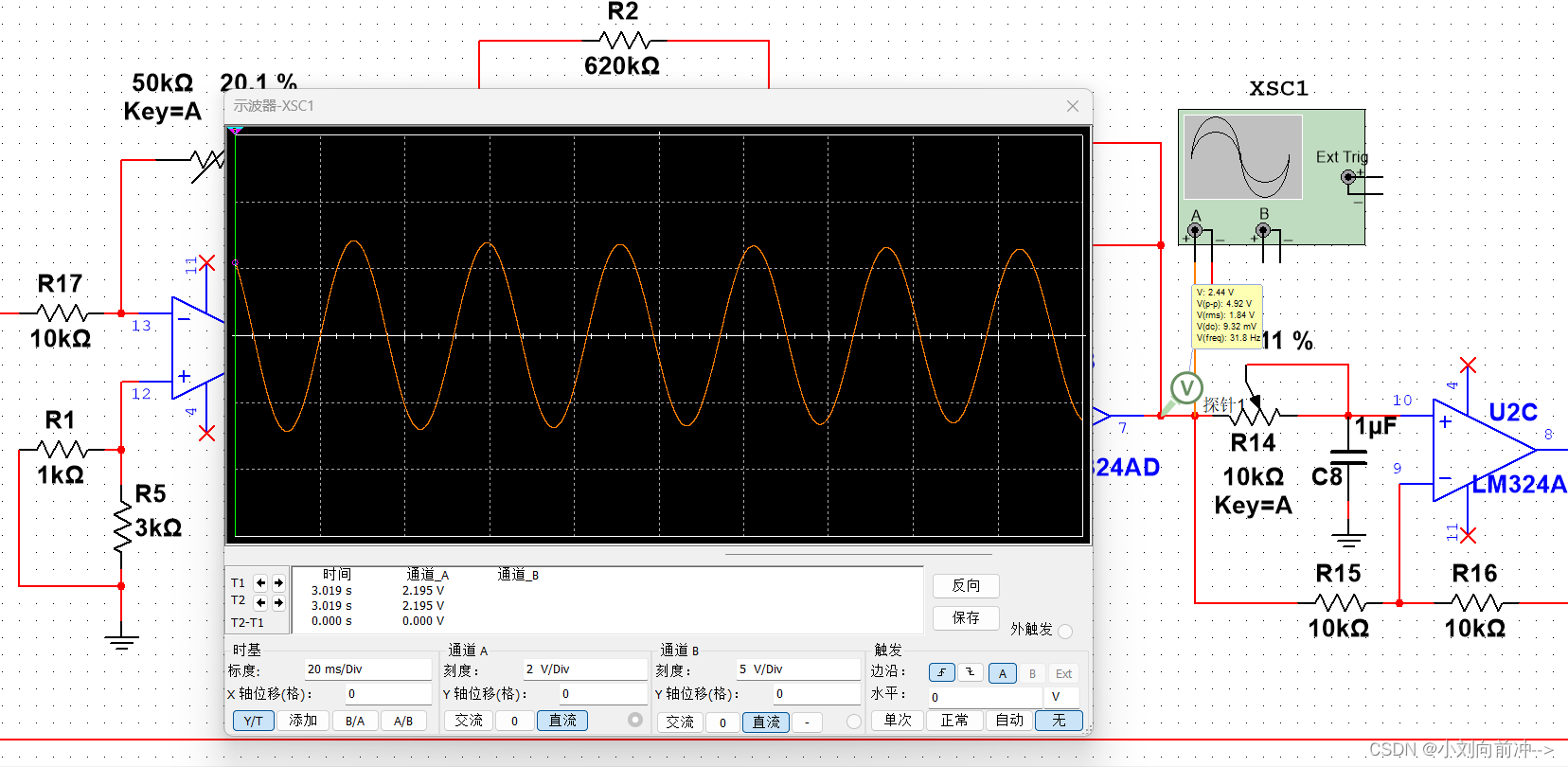
        可以看到，此时输出稳定正弦波，正弦波频率为31.8hz，完全符合之前理论上推导输入为0时微分方程的解，即方程的齐次解。

（2）微分方程非齐次解的部分

①接入正弦波

将反相比例的同相输入端接地改为输入信号输入端，并接入产生好的正弦波。

点击运行，观察输出端齐次解的波形和频率：

齐次解的输出波形为稳定的马鞍波波形，与题目中所给的参考解:

两个余弦波的叠加完全一致，观察输出探针显示马鞍波的频率为31.8hz，也与

        表达式对应完全一致。并且对照之前matlab模拟计算机解微分方程仿真结果，与之完全对应，说明了电路仿真的正确性。

②接入三角波

点击运行，观察输出端齐次解的波形和频率：

        可以看到，输出波形为一个类似正弦波，解的频率为31.8hz，与理论完全相符合。并且对照之前matlab模拟计算机解微分方程仿真结果，与之完全对应，说明了电路仿真的正确性。

3.电路焊接实际验证

（1）实物洞洞板焊接

（2）实物实验室示波器观测

 产生正弦波

产生三角波

同频同相的三角波和正弦波

 模拟计算机-接地产生正弦波(31.8hz)

模拟计算机-接入正弦波，产生马鞍波

模拟计算机-接入三角波，产生类似正弦波

4.模拟计算机解微分方程结果综合分析

Matlab仿真结果

Multisim仿真结果

实际焊接结果