---

一、基本概念

一些针对ARIMA模型的预备知识，若只需应用ARIMA模型求解可跳至第二节

1、$AR(p)$模型

$AR$模型又称为自回归模型，是一种处理时间序列预测的方法。它描述了当前值与历史值之间的关系，用变量自身的历史数据对自身进行预测。

一般的$p$阶自回归模型$AR(p)$定义为：
$$\begin{array}{rl}{x}_t& ={\varphi }_0+{\varphi }_1{x}_{t-1}+{\varphi }_2{x}_{t-2}+...+{\varphi }_p{x}_{t-p}+{\mu }_t\\ {\varphi }_p& \ne 0\end{array}$$
由上述公式可以看出一个时间点的预测值可以由其过去某个时间段内的所有历史值的线性组合表示。其中：
$p$表示：所使用的时间滞后的数量，即用前$p$期的历史值来预测当前值；
${\varphi }_i$表示：是第$i$个滞后项的系数，代表了第$i$个滞后项对当前时间点的相对影响力；
$x_{t-i}$表示：时间点$x_t$前第$i$个历史数据值；
${\mu }_t$表示：时间点t的误差项，严格的自回归模型中误差项是一个白噪声${\mu }_t={\epsilon }_t$。

2、$MA(q)$模型

$MA(q)$模型又称为移动平均模型，它描述的时间序列当前值与历史数据没有关系，而是只依赖过去的预测误差的累加。这种过去的预测误差可以表示为过去一段时间内，不可预料的各种偶然事件或突发事件。
一般的$q$阶移动平均模型$MA(q)$定义为：
$$\begin{array}{rl}{x}_t& =\mu +{\epsilon }_t-{\theta }_1{\epsilon }_{t-1}-...-{\theta }_q{\epsilon }_{t-q}\\ {\theta }_q& \ne 0\end{array}$$
由上述公式可以看出，一个时间序列是过去若干期噪声的加权平均，即当前的观察值是由过去的白噪声通过一定的线性组合得到的。其中：
$\mu$表示：时间序列的均值或期望值；
${\epsilon }_{t-i}$表示：$i$个时刻前的白噪声项；
${\theta }_i$表示：对应的白噪声对当前时间点的影响程度；
$q$表示：前$q$个白噪声被纳入模型。

3、$ARMA(p,q)$模型

$ARMA(p,q)$模型又称为自回归移动平均模型，是$AR(p)$模型与$MA(q)$模型的结合。他表示时间序列的当前值可由其自身的历史值以及随机扰动项来解释。
$$x_t={\varphi }_0+{\varphi }_1{x}_{t-1}+...+{\varphi }_p{x}_{t-p}+{\epsilon }_t-{\theta }_1{\epsilon }_{t-1}-...-{\theta }_q{\epsilon }_{t-q}$$
注意：$ARMA$模型的数据必须是平稳序列。

4、$ARIMA(p,d,q)$模型

$ARIMA(p,d,q)$模型又称差分自回归移动平均模型，是$ARMA(p,q)$模型与差分法的结合，其中$d$是需要对数据进行差分的阶数。由于$ARMA$模型要求数据是平稳序列，需要对非平稳数据进行差分运算化为平稳数据再进行分析，因此发展出$ARIMA$模型。

注意：$ARIMA$模型的数据也必须是平稳序列。

---

二、$ARIMA(p,d,q)$模型求解

1、数据准备

使用jupyter notebook来编写python程序。
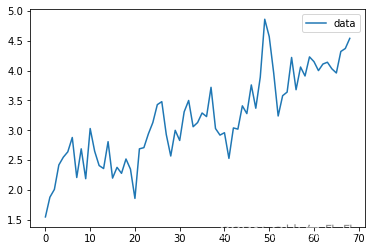
首先引入库，读取数据并进行可视化操作。

import pandas as pd
import numpy as np
import matplotlib.pylab as plt
data = pd.read_excel('F:\\代码学习\\CSDN博客\\ARIMA模型\\时序数据.xlsx') 
data.plot()
plt.show

2、平稳性检验

由于ARIMA模型只能使用平稳数据建模，因此需要对原始数据进行平稳性检验。本文使用单位根检验的方法检验数据的平稳性。单位根检验有诸多方法，其中较为经典是ADF检验。平
ADF检验可以通过python中的 statsmodels 模块，这个模块提供了很多统计模型。

#平稳性检验
#自定义函数用于ADF检查平稳性
from statsmodels.tsa.stattools import adfuller as ADF
def test_stationarity(timeseries,alpha):#alpha为检验选取的显著性水平
    adf=ADF(timeseries)
    p=adf[1]#p值
    critical_value=adf[4]["5%"]#在95%置信区间下的临界的ADF检验值
    test_statistic=adf[0]#ADF统计量
    if p<alpha and test_statistic<critical_value:
        print("ADF平稳性检验结果：在显著性水平%s下，数据经检验平稳"%alpha)
        return True
    else:
        print("ADF平稳性检验结果：在显著性水平%s下，数据经检验不平稳"%alpha)
        return False

使用自定义函数test_stationarity()对原始数据进行ADF单位根检验，得到的结果为“ADF平稳性检验结果：在显著性水平0.05下，数据经检验不平稳”。

test_stationarity(data['data'],0.05)#对原始数据进行ADF单位根检验

因此，原始时序数据是非平稳数据，需要对其进行差分运算化为平稳数据。这里使用dropna()函数去除差分后数据第一行的NaN值。得到的结果为“ADF平稳性检验结果：在显著性水平0.05下，数据经检验平稳”。

data['diff1']=data['data'].diff(1)#一阶差分
test_stationarity(data['diff1'].dropna(),0.05)#对一阶差分数据进行单位根检验

3、白噪声检验

在得到平稳数据后，需要对平稳数据进行白噪声检验，验证序列中有用信息是否已经被提取完毕。若序列是白噪声序列，说明序列中有用信息已经被提取完，只剩随机扰动。白噪声序列没有分析价值，应该被舍弃。
本文使用Ljung-Box检验白噪声，即LB白噪声检验方法。通过statsmodel库调用acorr_ljungbox()函数实现LB白噪声检验。

#自定义函数用于LB白噪声检验
from statsmodels.stats.diagnostic import acorr_ljungbox 
def test_white_noise(data,alpha):#alpha为检验选取的显著性水平
    [[lb],[p]]=acorr_ljungbox(data,lags=1)
    if p<alpha:
        print('LB白噪声检验结果：在显著性水平%s下，数据经检验为非白噪声序列'%alpha)
    else:
        print('LB白噪声检验结果：在显著性水平%s下，数据经检验为白噪声序列'%alpha)  

对原始序列的一阶差分数据进行LB白噪声检验，得到的结果为“LB白噪声检验结果：在显著性水平0.05下，数据经检验为非白噪声序列”。

test_white_noise(data['diff1'].dropna(),0.05)#对一阶差分数据进行白噪声检验

故原始时间序列的一阶差分数据是平稳非白噪声序列，可以用ARIMA模型对时间序列进行预测。

4、模型定阶

4.1 根据ACF、PACF图进行定阶

ARIMA模型定阶是确定模型中的参数p,q值。模型定阶可以通过自相关图ACF和偏自相关图PACF初步定阶，这种定阶方法比较直观但普适性较差。
自相关函数 ACF 描述的是时间序列观测值与其过去的观测值之间的线性相关性。
偏自相关函数 PACF 描述的是在给定中间观测值的条件下，时间序列观测值预期过去的观测值之间的线性相关性。
如果ACF拖尾，PACF在某阶后截尾，那么应该考虑AR模型，PACF截尾的阶数可能是AR模型的阶数。如果ACF在某阶后截尾，PACF拖尾，那么应该考虑MA模型，ACF截尾的阶数可能是MA模型的阶数。如果ACF和PACF都拖尾，那么应该考虑ARIMA模型。如果ACF和PACF图像都不呈现拖尾状态，那么时间序列可能是一个白噪声序列。

通过statsmodel库引入plot_acf与plot_pacf函数来绘制ACF图与PACF图。

from statsmodels.graphics.tsaplots import plot_acf,plot_pacf
plot_acf(data['diff1'].dropna(),lags=30)#lags表示选择的滞后阶数
plot_pacf(data['diff1'].dropna(),lags=30)

如图所示，ACF图和PACF图都可以看作拖尾，此时ACF和PACF图像无法帮助我们确定参数p和q的具体值，但能确认p和q一定都不为0。

4.2 网格搜索法定阶

根据ACF与PACF图我们获得了可能的p和q值的初步想法——二者都不为零。但上述方法并未给我们准确的答案，这就需要我们使用模型选择准则（AIC或BIC准则）来确定模型参数。
AIC 信息准则即 Akaike information criterion，是衡量统计模型拟合优良性的一种标准。AIC越小表示模型拟合的越好。

from statsmodels.tsa.arima.model import ARIMA
import itertools
#自定义ARIMA模型的网格搜索函数
def ARIMA_search(data,diff):
    #data表示网格搜索定阶的数据
    #diff表示差分数量
    p=range(1,3)#参数p的搜索范围
    q=range(1,5)#参数q的搜索范围
    d=[diff]
    pdq=list(itertools.product(p,d,q))
    #itertools.product()得到的是可迭代对象的笛卡儿积
    #list是python中是序列数据结构，序列中的每个元素都分配一个数字定位位置
    params=[]
    results=[]
    grid=pd.DataFrame()
    for param in pdq:
        #建立模型
        mod= ARIMA(data,order=param)
        #实现数据在模型中训练
        result=mod.fit()
        print("ARIMA{}-AIC:{}".format(param,result.aic))
        #format表示python格式化输出，使用{}代替%
        params.append(param)
        results.append(result.aic)
    grid["pdq"]=params
    grid["aic"]=results
    print(grid[grid["aic"]==grid["aic"].min()])#选择使AIC最小的参数组合

对原始序列的一阶差分数据进行网格搜索定阶，得到的定阶结果如下图所示。

import warnings
warnings.filterwarnings("ignore")#忽略输出警告
ARIMA_search(data['diff1'].dropna(),1)

故定阶结果为$ARIMA(1,1,4)$模型。

5、建立模型

根据定阶结果，对原始数据建立$ARIMA(1,1,4)$模型。输出该模型的描述性统计量如下。
注意！使用一阶差分数据定阶（因为其是平稳非白噪声序列），定阶后使用原始数据建立模型

#建立ARIMA模型
model=ARIMA(data['data'],order=(1,1,4))
ARIMA_m=model.fit()#训练模型
print(ARIMA_m.summary())#输出模型的描述性统计量

6、模型检验

使用在第三节中定义的白噪声检验函数test_white_noise()对模型的残差进行白噪声检验，得出的结果为“LB白噪声检验结果：在显著性水平0.05下，数据经检验为白噪声序列”。这说明模型中的有用信息提取充分，也就说明模型拟合效果较好，通过检验。

#模型检验
test_white_noise(ARIMA_m.resid,0.05)#ARIMA_m.resid提取模型残差，并检验是否为白噪声

7、模型拟合及误差分析

使用get_prediction函数拟合历史数据，得到的拟合曲线与置信区间如下图所示。

#模型拟合
pred=ARIMA_m.get_prediction(start=0,dynamic=False,full_results=True)
#获得置信区间
ci=pred.conf_int()
#历史数据拟合值
fittingdata=pred.predicted_mean
#画图
plt.plot(fittingdata,label="fitting data")
plt.plot(data['data'],label="base data")
plt.fill_between(ci.iloc[1:].index,ci['lower data'].iloc[1:],ci['upper data'].iloc[1:],color='grey',alpha=0.15,\
                 label="confidence interval")#画出置信区间
plt.legend(loc="best")#标签最佳显示
plt.title('ARIMA(1,1,4)')
plt.show

使用MSE、RMSE和MAE来评估模型拟合效果，得到的结果如下图所示，拟合效果较好。

#历史数据拟合误差分析
from sklearn.metrics import mean_squared_error as mse
from sklearn.metrics import mean_absolute_error as mae
print("1) MSE:{}".format(mse(data['data'],fittingdata)))
print("2) RMSE:{}".format(np.sqrt(mse(data['data'],fittingdata))))
print("3) MAE:{}".format(mae(data['data'],fittingdata)))

8、模型预测

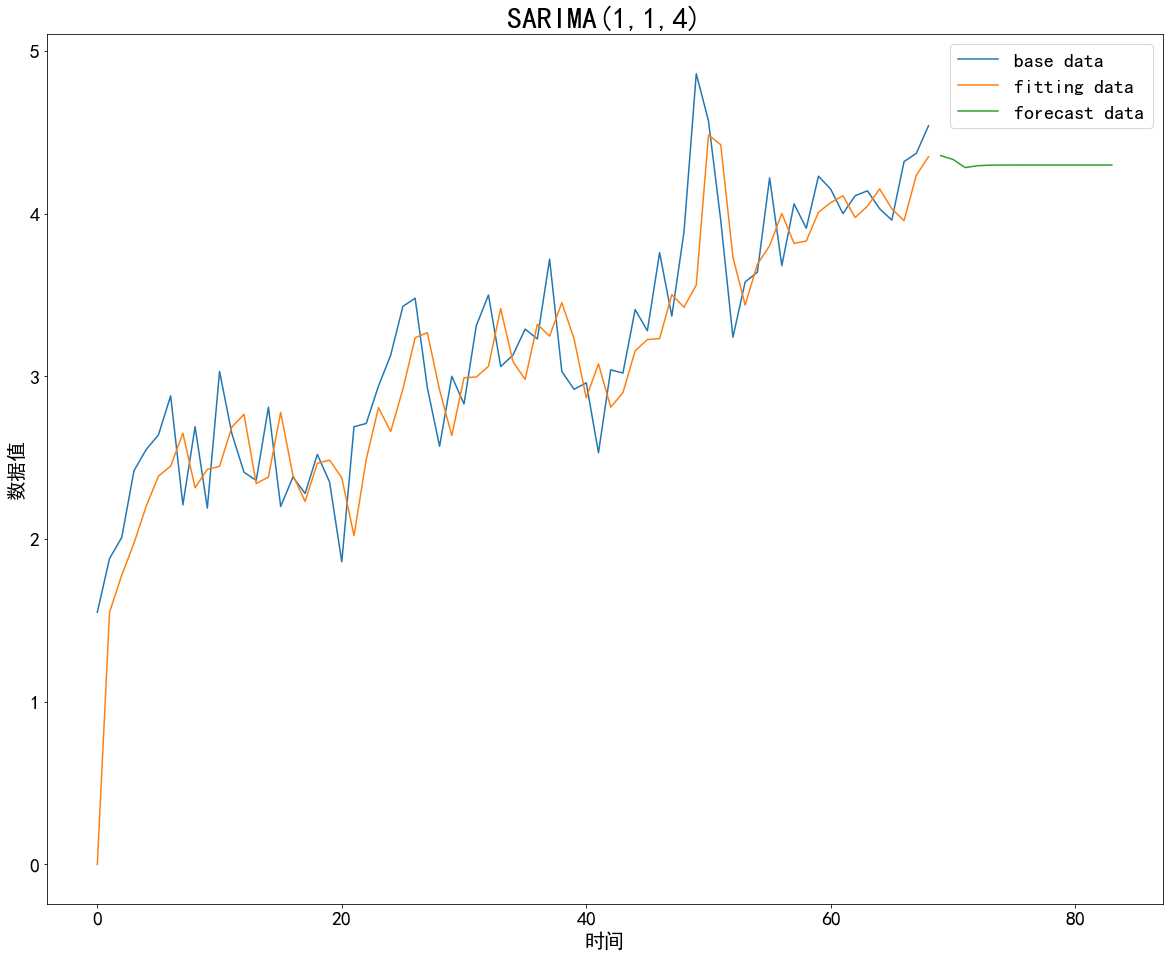
使用get_forecast()函数对原始时间序列进行未来15天数据值的预测。结果如下图所示。

plt.rcParams["font.sans-serif"]=["SimHei"]#用来正常显示中文标签
#预测未来15天的数据值
fig,ax=plt.subplots(figsize=(20,16))
data['data'].plot(ax=ax,label="base data")#原始数据
fittingdata.plot(ax=ax,label="fitting data")#拟合数据
forecast=ARIMA_m.get_forecast(steps=15)#获得未来15天的数据值
forecast.predicted_mean.plot(ax=ax,label="forecast data")
ax.legend(loc="best",fontsize=20)#显示标签
ax.set_title("SARIMA(1,1,4)",fontsize=30)
ax.set_xlabel("时间", fontsize=20)
ax.set_ylabel("数据值",fontsize=20)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.show