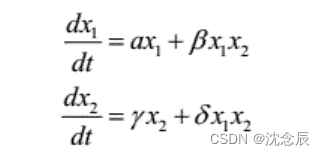
论文研究2——李雅普诺夫（Lyapunov）稳定性分析
本文简单的对李雅普诺夫（Lyapunov）第二法的判稳流程进行了介绍，并给出了一些例题
文章共3,947字 · 阅读需要大约14分钟
前提：本文只讨论自治系统（时不变系统），以下的稳定性分析都基于这一前提上。且本文的只讨论李雅普诺夫第二法的判稳流程。
目录
1.基本概念
（1）李雅普诺夫的两种方法
①李雅普诺夫第一方法（间接法）
对于线性系统，只须求出系数矩阵的特征值即可判断其稳定性。
对于非线性系统，则由若干过程组成，其中每个过程都要用到具体的形式。由系统的动态方程来找出其一次近似的线性化方程，在通过对线性化方程的稳定性的分析而给出原非线性系统在小范围内稳定性的有关信息。
②李雅普诺夫第二方法（直接法）
不需要引入线性近似，而直接由系统的运动方程出发，通过构造一个类似于能量的Lyapunov函数，并分析它和其一次导数的定号性而获得系统稳定性的有关信息
能量函数：状态和时间的标量函数，又称为李雅普诺夫函数，记作V(x,t)，这里我们不讨论时间，所以是V(x)
（2）线性与非线性系统在判稳上的一些差异
①平衡点
首先我们需要知道，=0时的状态，就是系统的平衡点。
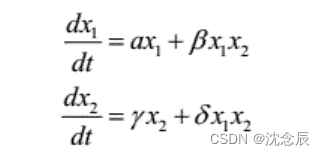
让这两个式子=0，就可以得出该系统的平衡点。
对于渐近稳定的线性系统而言，其平衡点只有一个，而且平衡点稳定时，系统一定是稳定的，但非线性系统不是这样的，因为非线性系统有的会有好几个平衡点，而判断非线性系统稳定时实际是指某一个平衡点的稳定性，不能笼统地说系统是稳定的还是不稳定的。
②初始条件的影响
线性系统的稳定性只取决于系统本身的结构和参数，与外作用和初始条件无关。而非线性系统平衡点处的稳定性不仅与系统本身的结构和参数有关，还与系统的初始条件有关系。
2.第二法的判稳流程
李雅普诺夫第二法的基本思想是，通过构建一个称为"李雅普诺夫函数"的函数来评估系统状态的演化，从而判断系统的稳定性。李雅普诺夫函数判稳的基本流程为：
（1）确定平衡点
首先需要确定动态系统的平衡点或者稳定状态，即系统处于此状态时不再发生变化，所有变量的导数或增量为零。（就是上面所说的平衡点求法）
（2）构造李雅普诺夫函数
首先，我们需要选择一个合适的李雅普诺夫函数，这是一个标量函数，通常表示为V(x)，其中x是系统状态向量。李雅普诺夫函数的选择通常是根据具体问题和系统的特性来确定的。（构造的方法有很多种，第三部分会简单说一下）构造出的函数需要注意两点：
①李雅普诺夫函数V(x)必须是非负的，即对于系统的每个状态x，V(x) > 0。
②李雅普诺夫函数在系统的稳定点（平衡点）处为零，即V(0) = 0。
（3）计算李雅普诺夫函数的导数
接下来，计算李雅普诺夫函数V(x)对时间的导数，即dV(x)/dt。这个导数描述了李雅普诺夫函数在系统状态空间中的变化率。
这里简单说一下怎么求：V(x)分别对x1,x2求导，然后两者相加，最后将
和
带入即可
可以得到——》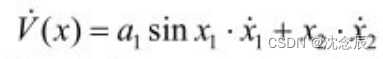
将
带入，最终得出
（4）评估导数的符号
检查导数dV(x)/dt的符号。如果对于系统的每个状态x，导数都是负的或者小于等于零的，即dV(x)/dt ≤ 0，那么李雅普诺夫函数是一个下降函数。这意味着系统状态在时间内趋向于减小，这是稳定性的一个指示。具体可以根据符号分为以下几种情况：
①如果对于系统的每个状态x，dV(x)/dt < 0，那么系统是全局渐近稳定的，意味着系统状态会收敛到某个有限的区域。
②如果对于系统的每个状态x，dV(x)/dt ≤ 0，但不全为负，那么系统是渐近稳定的，但可能会有一些特定的状态或轨迹是边界稳定的。
③如果存在某些状态x，使得dV(x)/dt > 0，那么系统是不稳定的，因为至少有一些状态会趋向于增加。
也可以参考这篇文章：李雅普诺夫稳定性理论
3.李雅普诺夫函数的构造方法
（1）线性定常系统
①构造方法
②相关例题
（2）非线性自治系统
①构造方法
②相关例题
第一题：
第二题：
（如有侵权，请联系我进行删除，多谢！）
旨在为数千万中国开发者提供一个无缝且高效的云端环境，以支持学习、使用和贡献开源项目。
更多推荐
39
0- 0
已为社区贡献3条内容
所有评论(0)