Yalmip入门教程(4)-约束条件定义的相关函数

博客中所有内容均来源于自己学习过程中积累的经验以及对yalmip官方文档的翻译：https://yalmip.github.io/tutorials/这篇博客将详细介绍yalmip工具箱中约束条件定义及计算等相关函数的用法。

文章共4,263字 · 阅读需要大约15分钟

一键AI生成摘要，助你高效阅读

问答

配电网和matlab

5374人浏览 · 2023-08-03 23:36:44

配电网和matlab · 2023-08-03 23:36:44 发布

博客中所有内容均来源于自己学习过程中积累的经验以及对yalmip官方文档的翻译：https://yalmip.github.io/tutorials/

这篇博客将详细介绍yalmip工具箱中约束条件定义等相关函数的用法。

1.约束条件定义的相关函数

1.1 alldifferent函数

alldifferent函数用于表示某个矩阵或向量中所有元素都不相同，使用语法如下：

F = alldifferent(X)

其中，X为决策变量，F为约束条件，表示X中所有元素都不同。

下面是一个代码示例，可以使用alldifferent函数产生整数1-5的一组排列：

x = intvar(1,5);
F = [alldifferent(x), 1<=x<=5];
optimize(F)value(x)

运行结果如下：

ans =

1 5 4 2 3

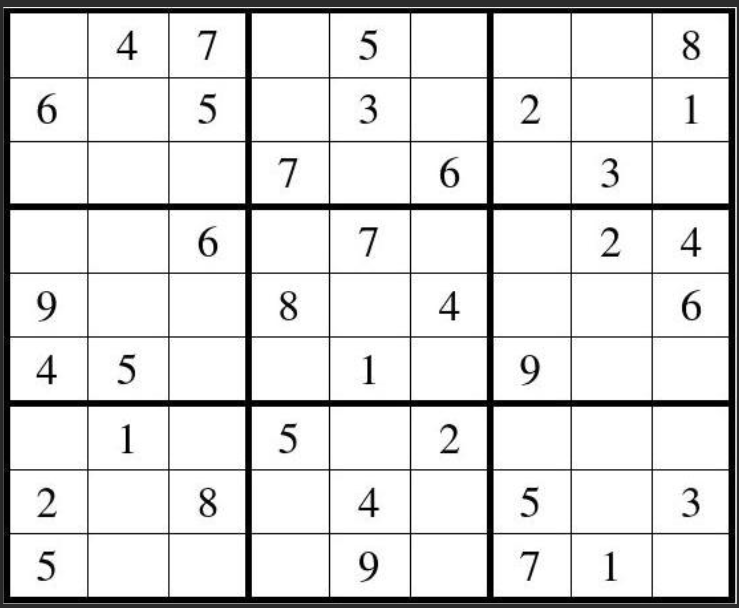
图1 一个数独问题

合理地使用alldifferent函数解决实际的优化问题，可以大大降低建模的难度，例如，上一篇博客中提到的数独问题，就是要使得数组中每一行，每一列以及每一个3×3的子块中的数字从1-9各不相同，那么使用alldifferent函数很方便地完成建模。针对图1所示的数组问题，采用alldifferent函数进行建模的代码如下：

A0 = [
    0 4 7 0 5 0 0 0 8;
    6 0 5 0 3 0 2 0 1;
    0 0 0 7 0 6 0 3 0;
    0 0 6 0 7 0 0 2 4;
    9 0 0 8 0 4 0 0 6;
    4 5 0 0 1 0 9 0 0;
    0 1 0 5 0 2 0 0 0;
    2 0 8 0 4 0 5 0 3;
    5 0 0 0 9 0 7 1 0;
    ];

A = intvar(9,9,'full');

fixed = find(A0);
F = [1 <= A <= 9, A(fixed) == A0(fixed)];

for i = 1:3
    for j = 1:3
        block = A((i-1)*3+(1:3),(j-1)*3+(1:3));
        F = [F, alldifferent(block)];
    end
end

for i = 1:9
    F = [F, alldifferent(A(i,:))];
    F = [F, alldifferent(A(:,i))];
end


F = [F, sum(A,1) == 45, sum(A,2) == 45];
optimize(F);
value(A)

运行结果如下：

ans =

3 4 7 2 5 1 6 9 8

6 8 5 4 3 9 2 7 1

1 2 9 7 8 6 4 3 5

8 3 6 9 7 5 1 2 4

9 7 1 8 2 4 3 5 6

4 5 2 6 1 3 9 8 7

7 1 3 5 6 2 8 4 9

2 9 8 1 4 7 5 6 3

5 6 4 3 9 8 7 1 2

通过该函数的使用，可以非常快速地解决数独问题。但需要注意的是，由于alldifferent函数内部使用了大M法进行建模，因此为了提高问题的求解效率，需要用到该函数的变量最好要提前给定上下限。所以这份代码在最开始就令变量A位于区间[1,9]。此外，该函数一般只适用于整数变量，如果对连续型变量使用，模型可能会存在不可解的问题。

1.2 complements函数

在数学优化领域，互补性条件是一个非常重要的概念，在KKT条件，对偶变换，最值变换等理论中都有所应用，yalmip工具箱中的complements函数可用于互补性条件的建模，在这里只对该函数的用法进行介绍，不涉及相关原理。

互补性条件要求要求一对变量满足互补关系，即它们的乘积为零。这种情况下，其中一个变量的取值为零，就意味着另一个变量的取值为非零，它们之间存在一种互相排斥的关系，例如对于变量x1和变量x2，互补性条件可以写做：

x1≥0，x2≥0，x1×x2=0

complements函数的基本语法如下：

F = complements(Constraint1,Constraint2)

其中，Constraint1和Constraint2表示两个不同的约束条件，F表示他们形成的互补性条件。

例1：使用yalmip中的complements函数对下列约束条件进行建模：

y≥0，x+z≥1，y(x+z)=0

Matlab代码如下：

sdpvar x y z

F = complements(y >= 0, x+z >= 1)

和alldifferent函数一样，complements函数内部使用了大M法进行建模，因此为了提高问题的求解效率，需要用到该函数的变量最好要提前给定上下限。

1.3 cone函数

二阶锥规划(Second-Order Cone Programming, SOCP)是最常用的凸优化之一，对于含二次约束的非线性规划，可以通过二阶锥松弛将其转为凸优化问题，具体原理可以查看相关资料进行学习，这里不再赘述，只重点讲解函数用法。该函数基本语法为：

c = cone(x,y)

这段代码表示了下面形式的二阶锥约束：

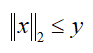
1.4 iff函数

iff函数用于表示两个约束之间的等价关系，其标准语法为：

F = iff(A,B)

约束F的含义为：当约束A成立时，约束B也成立，当约束B成立时，约束A也成立。

例2：使用yalmip工具箱中的iff函数对下列约束条件进行建模

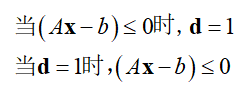
使用iff函数对其进行建模的代码如下：

A = 2;
b = 0.5;
x = sdpvar(1);
d = binvar(1);
F = iff(d,A*x <= b);

实际上，iff也可以用”==”符号进行替换，下面的代码一样可以实现例2中的约束，和iff函数的建模完全等价：

A = 2;
b = 0.5;
x = sdpvar(1);
d = binvar(1);
F = [d == A*x <= b];

实际应用的过程中可以根据自己的需要合理地选择两种不同的方式。

1.5 ismember函数

ismember函数用于约束变量的取值位于某个离散集中，标准语法如下：

F = ismember(x,Y)

其中x表示变量，Y表示离散集合。例如要使连续变量x取值只能为{0.5, 1, 1.5, 2}其中一个数，可以用ismember函数表示为：

sdpvar x

F = ismember(x,[0.5 1 1.5 2]);

巧妙地应用ismember函数，可以提升优化问题求解的效率，更多的应用之后会展开来讲。

1.6 isoutside函数

需要注意的是，isoutside函数是新版yalmip工具箱中给出的函数，如果在使用时提示找不到函数或变量，说明下载的不是最新版工具箱，更新一下即可。isoutside函数的标准用法如下：

Model = isoutside(P)

P表示一组线性不等式约束，Model也是一组约束，但是Model所表示的可行域将位于P表示的可行域外部。这么说可能非常难理解，举个简单的例子。假设约束P为：

P = [1 <= x <=2 , 2 <= y <=5];

显然该约束所表示的可行域为一个矩形，那么isoutside(P)所表示的可行域则为矩形的外部。在yalmip工具箱中，重写了可以应用于lmi类型变量的plot函数，可以绘制出线性约束条件所表示的可行域，约束P和isoutside(P)表示的可行域对比如下：

sdpvar x y
P = [1 <= x <= 2 , 2 <= y <= 5];
 
S = isoutside(P);
figure
plot(P,[],[],[],sdpsettings('plot.shade',0.1));
figure
plot(S,[],[],[],sdpsettings('plot.shade',0.1));

运行结果为：

图2 约束P所代表的可行域

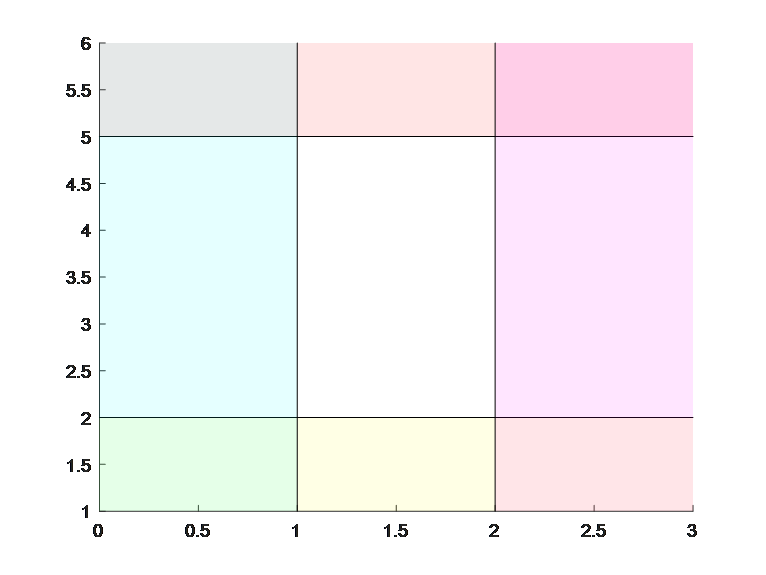图3 约束isoutside(P)所代表的可行域

isoutside函数在日常求解优化问题中也有很多用处，下面是一个例子：

例3：求坐标原点(0,0)到下列约束组成的五边形区域边界距离的最小值：

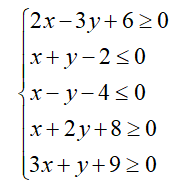
首先，我们利用针对lmi类型变量的plot函数，画出该可行域，如图4所示：

sdpvar x y
F = [2*x - 3*y + 6 >= 0 , ...
     x + y - 2 <= 0 , ...
     x - y - 4 <= 0 , ...
     x + 2*y + 8 >= 0 , ...
     3*x + y + 9 >= 0];
figure
axis([-3.5 3.5 -4.5 2.5])
plot(F,[],[],[],sdpsettings('plot.shade',0.1));

图4 例3中变量的可行域

问题中要求的是原点到该五边形区域边界距离的最小值，在已知约束F的情况下，似乎不好对目标函数进行建模。但是如果我们转换一下思维，也可以认为是求原点到F描述的可行域之外区域距离的最小值，这样就可以利用isoutside函数，很轻松地完成建模，matlab代码和结果如下：

sdpvar x y
F = [2*x - 3*y + 6 >= 0 , ...
     x + y - 2 <= 0 , ...
     x - y - 4 <= 0 , ...
     x + 2*y + 8 >= 0 , ...
     3*x + y + 9 >= 0];
 
F1 = isoutside(F);
optimize([F1, -3.5 <= x <= 3.5 , -4.5 <= y <= 2.5] , x^2 + y^2);
 
figure
axis([-3.5 3.5 -4.5 2.5])
plot(F,[],[],[],sdpsettings('plot.shade',0.1));
hold on;grid on
plot(value(x),value(y),'*')
r = sqrt(value(x^2 + y^2));
t = 0:0.01:2*pi;
plot(r*cos(t),r*sin(t),'--')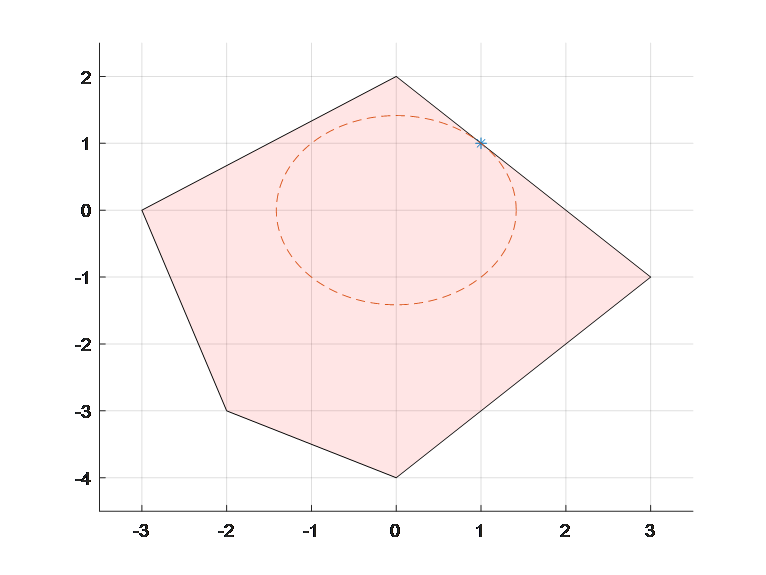

图5 可行域F边界上到(0,0)距离最小的点所在位置

1.7 uncertain函数

uncertain函数是利用Yalmip工具箱求解鲁棒优化的一个功能函数，用于将变量定义为不确定变量，之前我写过博客进行介绍，这里不再赘述，想要了解可以打开我之前的博客(https://blog.csdn.net/weixin_44209907/article/details/125691435)或者官方文档。

1.8 implies函数

implies函数是使用yalmip工具箱将非线性约束转为线性约束最常用的函数之一，作用是定义约束条件之间的逻辑关系，用法如下：

F = implies(A,B)

其中，A，B均为约束条件，F表示当约束条件A成立时，约束条件B也一定成立。(需要注意和iff函数的区别，iff函数也是定义两组约束之间的逻辑关系，但表示的是两者完全等价，而使用implies函数定义的约束则只能由A成立得到B成立，反之则不确定)。

在优化问题的约束条件含有逻辑关系、具有分段函数等情况时，采用implies函数可以方便地进行数学建模，下面是一个示例：

例4：使用yalmip工具箱对下列分段函数进行建模

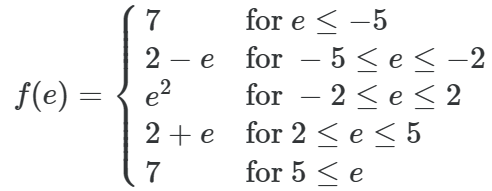
仅仅从逻辑上分析，可以使用matlab中的if-else语句完成这个函数的建模，代码如下：

sdpvar e
 
if e <= -5
    f = 7;
elseif e >= -5 && e <= -2
    f = 2-e;
elseif e>=-2 && e <= 2
    f = e^2;
elseif e>=2 && e <= 5
    f = 2+e;
elseif e >= 5
    f = 7;
end

但是在运行上面的代码一定会出现下列报错，这是因为sdpvar类型的变量不支持在if-esle语句中进行逻辑判断。

从 constraint 转换为 logical 时出现以下错误:

无法从 constraint 转换为 logical。

出错 test (line 3)

if e <= -5

为了实现分段函数建模，可以利用implies函数，matlab代码如下：

sdpvar e
sdpvar f
d = binvar(5,1);
 
Model = [sum(d) == 1,
implies(d(1), [e <= -5, f == 7]);
implies(d(2), [-5 <= e <= -2, f == 2-e]);
implies(d(3), [-2 <= e <= 2,  f == e^2]);
implies(d(4), [ 2 <= e <= 5,  f == 2+e]);
implies(d(5), [ 5 <= e,       f == 7])];

在建模时，引入了一个5维的0-1变量d，限制sum(d)=1表示五种情况只能取得其中一种。这样就可以简单直观地完成分段函数建模。implies函数还有更多用法，这里不再赘述。此外，implies函数内部也是使用大M法完成建模的，因此使用implies函数时最好保证涉及的变量都指定了上下限。