【现代机器人学】学习笔记二:刚体运动
这一节内容最开始在学之前是有些不屑的,这些坐标变换的内容天天都在玩,有什么复杂的?高翔博士的14讲貌似讲这些内容只用了几页。 不过认真一读才发现自己自大肤浅了。之前我在北大研究院的时候,有一个实验室双聘的浙农林的老师,讲机器人尤其是机械臂相关内容的时候,经常提到旋量这一概念。不过我当时主要做机器人导航,主要做一些避障规划定位的事情,讲实话他讲的内容我听不太懂。只知道这个内容基本就是slam里面的齐
这一节内容最开始在学之前是有些不屑的,这些坐标变换的内容天天都在玩,有什么复杂的?高翔博士的14讲貌似讲这些内容只用了几页。 不过认真一读才发现自己自大肤浅了。
之前我在北大研究院的时候,有一个实验室双聘的浙农林的老师,讲机器人尤其是机械臂相关内容的时候,经常提到旋量这一概念。不过我当时主要做机器人导航,主要做一些避障规划定位的事情,讲实话他讲的内容我听不太懂。只知道这个内容基本就是slam里面的齐次变换的李代数,但为什么有旋量这个名字,又具体怎么用它,我自己不是很清楚。当时其实我也尝试着自己网上搜索过,网上的资料太散了,看的云里雾里,不明就里。后来因为跳槽等其他琐事,就没再继续下去。
不过学完这一章,也算是把包括旋量在内的整个刚体运动的不同表示形式了然于心了,而不仅仅是两个矩阵下标相同就合并这么简单。
接下来我会主要着重写一些我在学习时认为的“新东西”,如果有也是做过SLAM,目前希望在机械臂控制上进行一些学习深入的朋友,相信这篇文章能带给你一些参考。
目录
旋转运动
矩阵约束
熟悉的表示形式,用矩阵R来表示,R的行列式为1,还是正交矩阵。R本身是有9个参数的,但是实际上它却只有3个参数是独立的,这是因为有六个约束:分别是每一列的元素平方和为1(3个),列向量两两正交(3个),因此就是6个约束。
有些人可能会讲了,行列式为1这个约束还没用到呢?这是因为行列式其实可以是正负1,这6个约束可以推导出行列式为正负一。而限制了行列式为1,是人为设定的,这样满足右手坐标系。实际上-1也可以,满足的是左手坐标系。所以不会影响它有3个参数是独立的这个条件。
简单的旋转直接手写旋转矩阵
slam的初学者容易忘记R中元素的含义,误以为这就是一个黑盒子矩阵,那么放两个简单的旋转让他写一个旋转矩阵,他就写不出来。(面试的时候遇到过这样的同学)

上图如果把a坐标系当作固定坐标系,那么b在a下面的表示就是:

这主要按列来看,xb和a坐标系的y轴正方向一致,所以Rb的第一列就是(0,1,0),多出的那个1就代表了a坐标系的y轴。yb和a坐标系的x轴正方向相反,所以Rb的第二列就是(-1,0,0),-1出现在第一位对应a坐标系的x轴,-1代表反向。z轴同理。
3.R可以表示姿态,也可以表示对参考坐标系的变换,也可以表示旋转某一个向量或者坐标系。
有两点非常重要的内容:
(1)对于一个Rsb,如果再来一个R左乘,R*Rsb代表在s系下进行旋转。如果R是右乘,Rsb*R代表在body系下进行旋转。
(2)绕单轴旋转,对应的矩阵:绕x轴,则位是1,绕y轴则是
位是1,绕z轴则是
位是1。那么以它为中心画十字,十字的其他地方是0。
那么剩下的地方,填cos和sin。
但这里有一个不一样的!就是绕y的运动:
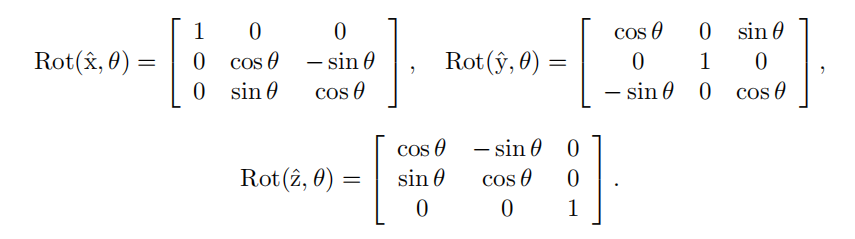
看起来绕y的运动,从对角线元素变号了。
这点我记得有个新来的学弟问我,不就绕轴旋转吗,难道绕的x还是y,有什么分别?
很多地方没写,也没讲为什么绕y轴的旋转矩阵公式不一样。
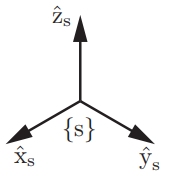
这当然是有分别的 ,随手画一个坐标系:
绕某个轴旋转意味着剩下的那两个轴构成一个平面,这里遵守右手坐标系,即横坐标向右,纵坐标向上。
另外我们再限制一下,假如xyz有个优先级,横坐标的优先级要低于纵坐标优先级。
从现在这个视角看过去,如果去掉x轴,剩下的y和z,看起来是横坐标是y,纵坐标是z。
去掉z轴,那么横坐标是x,纵坐标是y。
但是去掉y就不一样了,剩下一个x和z,x是向左的,z是向上的。那么这里变成一个左手坐标系了,所以y比较独特,不能按照原先的公式来算。
角速度
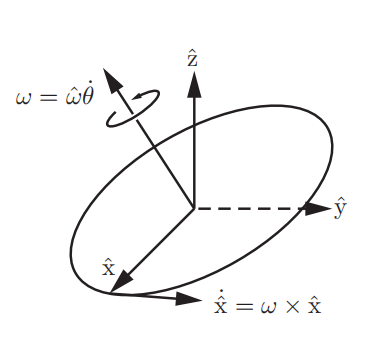
这个图比较关键,后续的一切推导均是从此图而来。
内容其实比较简单,绕轴w的运动叉乘xyz坐标轴,可以得到xyz轴的瞬时变化速度。那么这个东西其实就是旋转矩阵的导数。
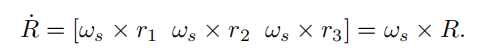
然后分别套用叉乘的反对称写法,然后再套用伴随性质
,最后就合并出两个公式:
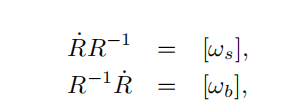
这个公式看起来有点难记,实际上也简单,就是一个R的导数和R的逆矩阵乘起来得到一个角速度的反对称表示。和 一样,表示导数的
在左边,就是得到ws,在右边就是wbody,以此辅助记忆。
指数坐标表示
指数坐标的推出还是从上面那个式子得到,这个公式无形之中就长得像一个线性常微分方程:
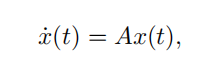 这个内容我记得是大一上学期高等数学(上)最后一章的基础内容,当时印象里学的是云里雾里的,算了一堆特解通解的,也不晓得有什么用。这下派上用场了。
这个内容我记得是大一上学期高等数学(上)最后一章的基础内容,当时印象里学的是云里雾里的,算了一堆特解通解的,也不晓得有什么用。这下派上用场了。
这个方程的含义就是,告诉你一个函数和它的导数的关系,你就可以把函数的表达式写出来。
那么这个方程的通解是:,其中x0是初始条件。(顺便提一嘴,只要x(t)是这个表达式的样子,解就是这个形式。但是不同的x(t),事实上x0不是同一个数,所以有的地方这里也用常数C来代替,但不意味着任何C都可以,不同的x(t)对应的C是不同的)
那么在 这里呢,A就是那个[w],x就是R,因此可以得到一个R的表达式:
,至于x0这个初始条件,对于旋转初始当然是单位阵,所以就是矩阵
,那么就这样得到了旋转矩阵的坐标表示形式。
, 书里为什么不用
,而是用的是
? 即
?
这就涉及到w和theta的含义了。可以理解为绕w轴转theta,也可以理解理解为在单位时间运动w*theta,也可以理解为在theta时间运动w,所以theta虽然是个绕
转动的角度,也可以代入到公式里当作时间看。
这个东西怎么计算呢?这里套用了高等数学中的矩阵指数,一顿化简,最后得到罗德里格斯公式:
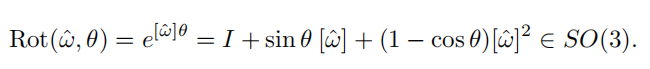
有的地方不这样写,比如在高翔博士的slam书里:
![]()
其实到底这个公式长什么样我完全不在意,因为平时我也压根不会自己写轮子去变换。所以我在面试的时候不会去问求职者,罗德里格斯公式怎么写,但是我会问他,罗德里格斯公式描述了谁和谁之间的变换?他需要答出来这个是旋转轴、角度 与 旋转矩阵的变换。
那么相反的过程,就是矩阵对数了:
这就不太唯一了,我把它列在这里以供查询,我不会尝试去记忆这个公式:
如果R是单位阵,θ是0,旋转轴w可以任意。
否则:
我只会记住R是单位阵,则w无所谓,R的迹是-1是多解的特殊情况。
其他旋转表示:
欧拉角(Euler angles ):
绕各个轴的运动,是在body系下的。所以是按照顺序右乘。(即按照转完以后的坐标系来转)
转的方式有两种,一种是三个转轴都不同,有六种,代表性的是ZYX转。另一种是第一个轴和第三个轴相同,同样也是六种,代表性的是ZYZ转。
不同的转法,和旋转矩阵R的变换关系也不一样,所以这里略过,反正平时也用不到。现用现查好了。
奇异性问题(万向锁):
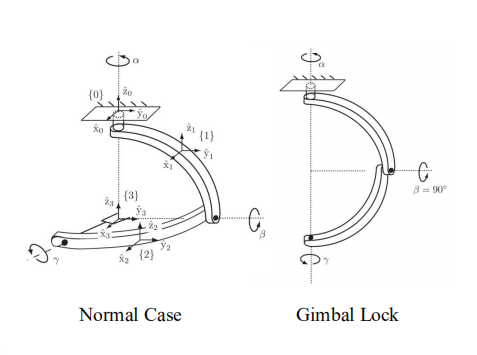
当β是90度的时候,左边那个机构的X轴实际上和Z轴共线了,转来转去也不会多一个自由度,这时候一个3自由度的机构就坍缩为了二自由度的结构,会导致奇异问题。
实际上轴角表示法都有这样的问题,只有旋转矩阵和四元数表示法不会有这样的问题。
Roll-pitch-yaw Angles :
这个是在space系下转的,每次沿着space固定系的X,Y,Z轴旋转。
因为是绕space转,因此左乘。那么乘下来的结果,和body系下的ZYX是一样的。
即:ZYX =
ZYX。
四元数:
这里借鉴加州大学滕瀚哲老师的课件。
一个实部,三个虚部。
有一些性质,重点如下:
1.q和-q代表相同的旋转。
2.和w与θ方便转换:

那这里为什么是θ/2呢?
这是因为,想尽量避免奇异性的问题。我们根据上面的公式可以看出来,如果绕的w轴只有两个数。例如(1,1,0),即沿着xy平面的一条直线转,那么q的最后一维q3就没有数字。
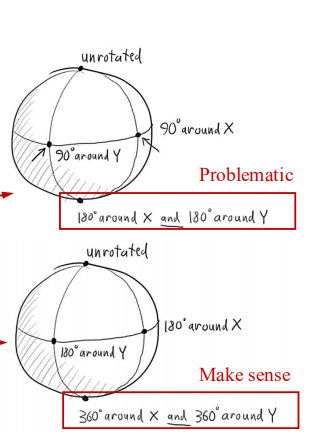
那么把q1,q2,q3画出来,我们把它当成一个球来看待。
假如有一个点落在南极,那我们从这个点出发,沿着q1转180度,或者沿着q2转180度,最后到达的都是相同的点,都是在北极。但是实际上刚体变换中,一个姿态沿着x轴转180和沿着y轴转180完全是不一样的。
所以把q0的单位设置为θ/2,那么从南极到北极,当θ=360度的时候,这个四元数球走的角度是360/2 = 180,在球面可以保证沿q1和q2走180度到达同一个位置,在现实中也可以保证一个姿态沿x轴转360和沿y轴转360是同一个姿态,实现这个四元数表达的逻辑上的自洽。
齐次变换
齐次变换是在旋转的基础上加了平移。它和旋转的知识点基本上是很像的,可以对应学习。
简单的齐次变换直接手写齐次矩阵:
旋转部分按照上面的方法手写,平移部分看新坐标系原点在旧坐标系下的位置。
值得注意:对于齐次变换,求逆矩阵,可以通过如下方式快速求逆,节省计算时间:
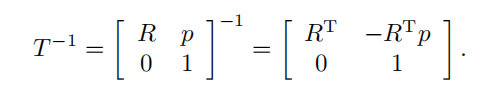
左乘右乘:
和旋转部分一样,有一个Tsb,左乘T,即T*Tsb代表在s系下的变换,右乘即Tsb*T代表在body系下的变换。
运动旋量定义
和上面旋转部分的一样:
和
一样,表示导数的
在左边,就是得到ws,在右边就是wbody,以此辅助记忆。
那么这里的 和
相乘,也是同样的规矩:
如果在左边,就是
,
在右边则是
。这就是旋量的矩阵表示形式。
值得一提的是:
vb表示在body坐标系下,刚体上过body坐标原点的那个位置的线速度。
vs表示:如果运动的刚体足够大,那么刚体上过固定坐标系s原点的那个位置在固定坐标系下的瞬时速度。
上面的表述挺拗口,大家理解意思即可。这本书的世界观里,所有的坐标系都是不动的,因此一有这种表述就很麻烦,要强调不是坐标系原点的速度,而是"刚体上恰好过坐标系原点的那个位置处的速度",哈哈。大家理解即可。
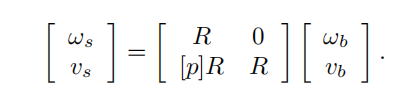
上式表示了两个旋量之间的变换,通过伴随变换矩阵Ad进行连接。
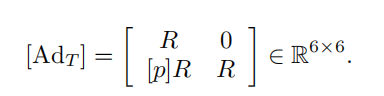
这个伴随变换矩阵有几个性质,罗列一下(我不想手打公式直接截图了,见谅):
力旋量
这里我直接跳到力旋量这里,因为我认为这里内容更加相关:
这块的内容实际上是动力学的内容,后续会用到,列出介绍:
半径向量r叉乘力f,可以得到力矩:
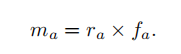 (力矩的变换仍然遵循用旋转矩阵可以变换:
(力矩的变换仍然遵循用旋转矩阵可以变换:![]() )
)
力旋量就是把力矩和力合在一起:
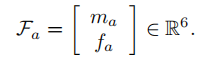
所以就有了空间力旋量 以及物体力旋量
,它俩之间可以通过上面提到的伴随变换矩阵建立联系:
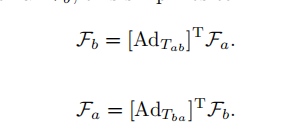
我们可以注意到:
内反外转置。比如左边是b,右边是a,那么中间就是ab,然后ad外面用T给它翻过来。
为什么有这个性质呢?这个是通过推导得到的:
同一系统功率相等。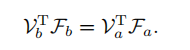 再根据
再根据![]() 正常这种旋量联立公式得到。
正常这种旋量联立公式得到。
需要记住Ad本身是没有转置特性的!!!它是需要求逆的。
力旋量这里可以用转置不是因为Ad可以转置,而是经过推导得到,且需要遵循“内反外转置”原则。
运动旋量的螺旋释义
这部分的内容初看比较抽象,记得当时看了好几次才理解。
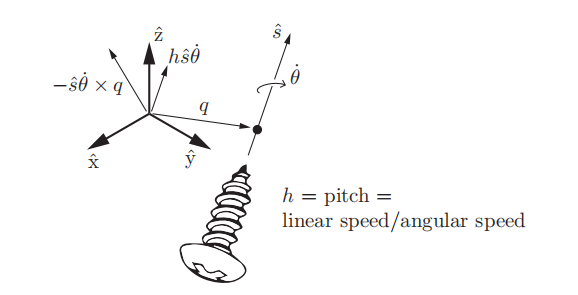
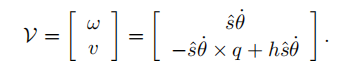
s表示螺旋轴的朝向,\dot{\theta}则表示绕轴转动的角速度大小。(注意这里是dot,上面是有一点的,表示角度的导数,角速度)。h表示节距,即线速度/角速度。q为轴上任意一点,用于配合s定位这根轴。
这里其实也好理解,主要费解的是下面的v。v是由两项构成的,表示绕螺旋轴的移动。这个需要看图,配合右手螺旋定则才能理解,我这里就不写了。另一项
是沿着轴的移动,这两项方向是正交的。
这里容易混淆的是,它多了一个螺旋轴的概念:。
那么也是[w,v],
也是[w,v],让人看了迷糊不已。其实S是V的一个正则化。
正则化的原则是:有w,用w正则化:
![]()
没有w,用v正则化:
![]()
也就是说,这样也是对的:
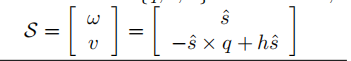
即满足条件:
虽然都用[w,v]表示,但是S中的w和v必须满足两个条件之一:
第一个:w模长为1
第二个:w=0,v的模长为1,即节距无限大。

都算出来以后,q为s轴上任意一点,根据上述公式反解即可。(可以应用向量a叉乘向量b等于a的反对称矩阵乘以b)
另外S和V一样,都可以用伴随变换矩阵Ad建立联系:
![]()
指数坐标与矩阵对数:
Chasles-Mozzi定理(查理-莫兹定理):任何刚体运动都可以通过绕空间某一固定螺旋轴S的运动描述。
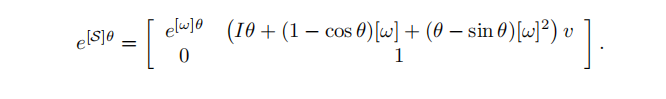
注意上面用的是螺旋轴S,即旋量的正则化形式。w的模长为1,或w=0,v的模长为1。
从螺旋轴S到齐次矩阵T的公式就长这样了,带入算就是了。
但是从T到S的,还是有些麻烦。
这里需要回顾上面讲的,从R到w和θ的过程。(即分为R是单位阵,以及R的迹是-1或不是-1的情况),所以认为w和θ已经可以求出来了。那么其实就差一个v了,v可以通过一个公式得到:

注意p在这里是齐次矩阵T里面的那个平移向量。
书的最后放了一张表格,我觉得这个表格实在整理的太好了,实在舍不得精简和删除,把它放在这里,以供查询。这张表格就基本代表了这节的所有内容了:


最后再强调一下,旋量中的
是沿轴的速度,指数表示中的
是
,是沿轴转过的角度,这二者可是不一样的,不要记混淆。
配套的代码实现,可以参考:【现代机器人学】学习笔记十三:配套代码解析
更多推荐
 已为社区贡献13条内容
已为社区贡献13条内容

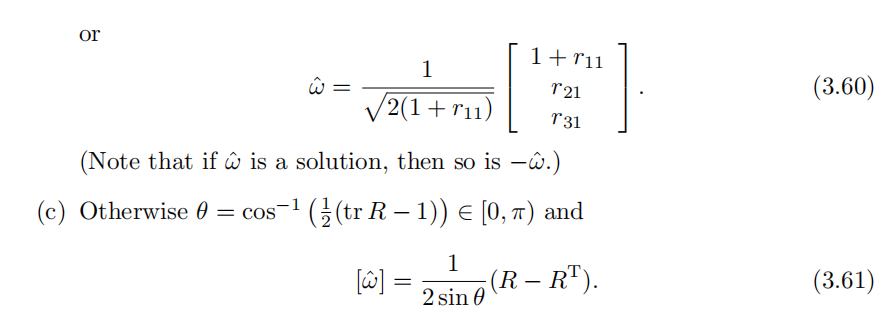
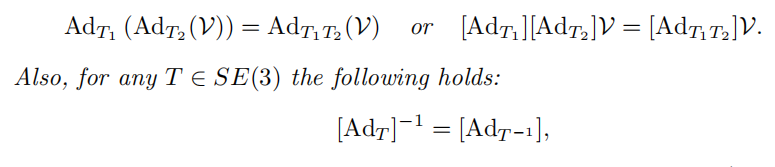








所有评论(0)