滤波器基础系列博客，传送门：

滤波器基础01——滤波器的种类与特性

滤波器基础02——滤波器的传递函数与性能参数

滤波器基础03——Sallen-Key滤波器、多反馈滤波器与Bainter陷波器

滤波器基础04——全通滤波器

滤波器基础05——巴特沃斯、切比雪夫与贝塞尔滤波器

滤波器基础06——滤波器设计软件

---

一. 电路元件的S域模型

通过引入拉式变化，将电路复杂的微分方程关系转化为简单的阻抗分压关系，大大简化了对电路频域性能的分析。

1.1 电阻R

电阻时域的伏安特性关系如下：
$$U_R\left(t\right)=R{i}_R\left(t\right)$$
取拉式变换有：
$$U_R\left(s\right)=R{i}_R\left(s\right)$$

这意味着电感在复频域或者说s域中保持不变，仍为R。

1.2 电感L

流过电感的电流不能突变，对于含有初始值$i_L\left(0_{-}\right)$的电感L，有如下关系：
$$u_L\left(t\right)=L\frac{d{i}_L\left(t\right)}{dt}\leftrightarrow U_L\left(s\right)=sL{I}_L\left(s\right)-L{i}_L\left(0_{-}\right)\leftrightarrow I_L\left(s\right)=\frac{U_L\left(s\right)}{sL}+\frac{i_L\left(0_{-}\right)}{s}$$

对于电流初始值为0的电感，其在s域中变为sL。

1.3 电容C

电容两端的电压不能突变，对应含有初始值$u_C\left(0_{-}\right)$的电容C，有如下关系：
$$i_C\left(t\right)=C\frac{d{u}_C\left(t\right)}{dt}\leftrightarrow I_C\left(s\right)=sC{U}_C\left(s\right)-C{u}_C\left(0_{-}\right)\leftrightarrow U_C\left(s\right)=\frac{I_C\left(s\right)}{sC}+\frac{u_C\left(0_{-}\right)}{s}$$
对于电压初始值为0的电容，其在s域中变为1/sC。

---

二. 滤波器的传递函数、幅频特性、相频特性与Bode图

2.1 传递函数

滤波器的传递函数定义为输出电压的拉式变换与输入电压拉式变换的比值，为：
$$H\left(s\right)=\frac{U_o\left(s\right)}{U_i\left(s\right)}$$
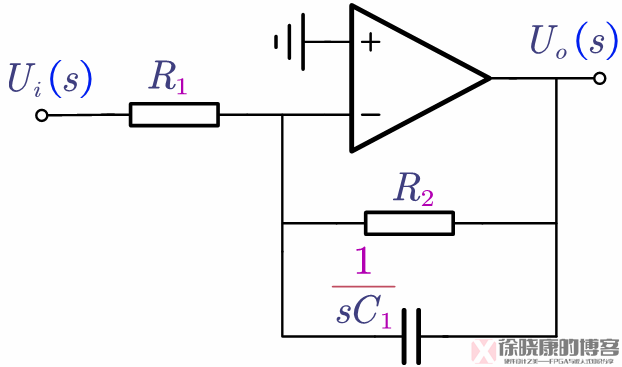
以一阶低通有源滤波器为例，其电路如下图所示：

其传递函数为：
$$H\left(s\right)=\frac{-\frac{R_2}{R_1}}{R_2{C}_{1}s+1}$$
令$A_m=-R_2/R_1\text{，}{n}_1=R_2{C}_1$，传递函数可写为：
$$H\left(s\right)=\frac{A_m}{1+n_{1}s}$$
这就是一阶低通滤波器的通用传递函数。对于更加复杂的滤波器，都可以写成如下通用形式：

$$H\left(s\right)=A_m\times \frac{1+m_{1}s+m_2{s}^2+...+m_m{s}^m}{1+n_{1}s+n_2{s}^2+...+n_n{s}^n}$$
其中，$n⩾m$，传递函数分母上s的最高次幂称为滤波器的阶数。

根据上式我们可以写出如下多种滤波器的通用形式，如：

将$s=0$与$s\to \infty$代入传递函数，就能理解低通、高通、带通、带阻的含义了。

2.2 幅频特性与相频特性

传递函数可写成实部加虚部的形式：
$$H\left(j\omega \right)=X\left(\omega \right)+jY\left(\omega \right)$$
输出信号与输入信号幅值比$A\left(\omega \right)$称为幅频特性，有：
$$A\left(\omega \right)=A_o/A_i=\left|H\left(j\omega \right)\right|=\sqrt{X^2\left(\omega \right)+Y^2\left(\omega \right)}$$

输出信号与输入信号相位之差$\phi \left(\omega \right)$为相频特性，有：
$$\phi \left(\omega \right)={\phi }_o-{\phi }_i=\angle H\left(j\omega \right)=\{\begin{array}{ll}\mathrm{arc}\tan \left(Y\left(\omega \right)/X\left(\omega \right)\right),& X\left(\omega \right)>0\\ 180°+\mathrm{arc}\tan \left(Y\left(\omega \right)/X\left(\omega \right)\right),& X\left(\omega \right)<0\\ 90°,& X\left(\omega \right)=0\text{，}Y\left(\omega \right)>0\\ -90°,& X\left(\omega \right)=0\text{，}Y\left(\omega \right)<0\end{array}$$

2.3 Bode图

横坐标按$\lg \omega$分度，单位为rad/s。幅频曲线纵坐标按：
$$dbA\left(w\right)=20\lg \left(A\left(\omega \right)\right)$$
线性分度，单位是分贝(dB)。对数相频曲线纵坐标按$\phi \left(\omega \right)$线性分度，单位为°。由此构成的坐标系称为半对数坐标系。构成的图称为Bode图。

根据传递函数就能画出滤波器的伯德图，可利用similink快速绘制，具体步骤可参考：

---

三. 滤波器的特征频率 $F_0$、品质因数Q与阻尼系数 $\alpha$

3.1 特征频率

在对滤波器长久的研究中，人们发现传递函数上存在一特殊的频率点对滤波器特性影响很大，称其为特征频率，符号为${\omega }_0$，单位为rad/s，对应以Hz为单位的特征频率为$F_0$。这两者都称为特征频率，表示的是同一个物理量，只是使用的单位不同。

对于一阶、三阶等奇数阶滤波器，特征频率是使得传递函数分母的实部等于虚部的点；

对于二阶、四阶等偶数阶滤波器，特征频率是使得传递函数分母的实部为0的点。

奇数阶以一阶低通滤波器为例，其传递函数为：
$$H\left(s\right)=A_m\times \frac{1}{1+n_{1}s}$$
奇数阶滤波器特征频率${\omega }_0$是满足传递函数的分母实部等于虚部的点，有：
$$1=n_1{\omega }_0\Rightarrow {\omega }_0=1/n_1$$
偶数阶以二阶低通滤波器为例，其传递函数为
$$H\left(s\right)=A_m\times \frac{1}{1+n_{1}s+n_2{s}^2}$$
代入$s=j\omega$到上式，有：
$$H\left(j\omega \right)=A_m\times \frac{1}{1-n_2{\omega }^2+j{n}_1\omega }$$
偶数阶滤波器特征频率${\omega }_0$是满足传递函数的分母实部为0的点，有：
$$1-n_2{{\omega }_0}^2\to {\omega }_0=\frac{1}{\sqrt{n_2}}$$

3.2 品质因数

另一个影响滤波器特性的参数称为滤波器品质因素，用字母Q表示，它定义为传递函数在特征频率处的幅值与$A_m$的比值。

对于上述二阶低通滤波器，有：
$$Q=\frac{A_m}{n_1{\omega }_0}/A_m=\frac{1}{n_1{\omega }_0}$$

3.3 阻尼系数

滤波器阻尼系数$\alpha$与品质因数Q表示的是同一个物理量，它们是互为倒数的关系，有：
$$\alpha =\frac{1}{Q}$$

---

四. 归一化滤波器

还是以低通二阶滤波器为例，在已知特征频率${\omega }_0$和品质因素Q之后，可得：
$$n_1=\frac{1}{Q{\omega }_0}\text{，}{n}_2=\frac{1}{{{\omega }_0}^2}$$
可见，在引入特征频率与品质因数后，就能将传递函数分母的系数用这两个有实际意义的物理量表示出来，有：

$$H\left(j\omega \right)=A_m\times \frac{1}{1+\frac{1}{Q{\omega }_0}j\omega +\frac{1}{{{\omega }_0}^2}{\left(j\omega \right)}^2}=A_m\times \frac{1}{1+\frac{1}{Q}j\frac{\omega }{{\omega }_0}+{\left(j\frac{\omega }{{\omega }_0}\right)}^2}$$
令$x=\omega /{\omega }_0$，那么上式可以改写为：
$$H\left(j\omega \right)=A_m\times \frac{1}{1+\frac{1}{Q}jx+{\left(jx\right)}^2}$$
x为频率与特征频率的比值，称为相对频率，是一个无量纲数。x = 1就表示频率等于特征频率点，这就是滤波器的归一化传递函数，通过引入相对频率，使频率的变化转换为相对频率的变化，此时滤波器特性转化为仅和品质因数Q有关。

滤波器的归一化在设计滤波器，确定不同截止频率的元件参数值时十分有用，这里不再展开。

---

五. 滤波器的截止频率、中心频率与带宽

5.1 截止频率

滤波器的截止频率定义为幅值比通带幅值低3dB时的频率，记为 ${\omega }_c$ 与 $f_c$ 。以一阶低通滤波器为例，其传递函数为：
$$H\left(s\right)=\frac{1}{1+s}$$
通带幅值为：
$$dBA\left(0\right)=20\lg \left(\left|H\left(0\right)\right|\right)=20\lg \left(1\right)=0dB$$
所以，截止频率处幅值的dB值为-3dB，有：
$$\begin{gathered} dBA\left({\omega }_c\right)=-3dB=20\lg \left(\left|H\left(j{\omega }_c\right)\right|\right)=20\lg \left(\frac{1}{\sqrt{1+{{\omega }_c}^2}}\right)=-10\lg \left(1+{{\omega }_c}^2\right) \\ \Rightarrow 1+{{\omega }_c}^2=10^{0.3}\Rightarrow {\omega }_c=\sqrt{10^{0.3}-1}=1 \end{gathered}$$
显然$20\ast \lg \left(0.707\right)=-3$，所以截止频率处的幅值为通带幅值的0.707倍。功率比 = 幅值比的平方，截止频率处信号功率为通带功率的 0.707 X 0.707 = 0.5倍，所以截止频率也可以描述为功率下降为通带功率一半的频率点。

一般来说，截止频率与特征频率是不同的频率点，但对于上述一阶低通滤波器，两频率是一个点。

实际设计滤波器时，通常会先预设好截止频率，所以，明确截止频率、特征频率、品质因数这三者的关系就能在确定截止频率后，快速确定后两者的数值，从而确定滤波器参数。

定义截止频率与特征频率的比值为K，有：
$$K=\frac{{\omega }_c}{{\omega }_0}$$
根据二阶低通滤波器传递函数：
$$H\left(j\omega \right)=A_m\times \frac{1}{1+\frac{1}{Q}j\frac{\omega }{{\omega }_0}+{\left(j\frac{\omega }{{\omega }_0}\right)}^2}$$

$$\begin{gathered} \left|H\left(j{\omega }_c\right)\right|=\left|A_m\times \frac{1}{1+\frac{1}{Q}j\frac{{\omega }_c}{{\omega }_0}+{\left(j\frac{{\omega }_c}{{\omega }_0}\right)}^2}\right|=\left|A_m\times \frac{1}{1-K^2+j\frac{K}{Q}}\right|=\frac{1}{\sqrt{2}}\left|A_m\right| \\ \Rightarrow \sqrt{{\left(1-K^2\right)}^2+{\left(\frac{K}{Q}\right)}^2}=\sqrt{2}\Rightarrow K=\frac{\sqrt{4Q^2-2+\sqrt{4-16Q^2+32Q^4}}}{2Q} \end{gathered}$$

所以，对于二阶低通滤波器，在Q确定时，K的值也就确定了即截止频率与特征频率的比值就确定了。通过这一点，我们先预设截止频率，然后确定Q值，这时就能根据公式推出特征频率，进而确定传递函数。以下给出一些典型的Q值对应的K值。

Q	0.4	0.5	0.6	0.7071	0.8	1	1.2	1.5	2.0
K	0.4278	0.6436	0.8271	1	1.1146	1.2720	1.3590	1.4299	1.5510

5.2 中心频率

中心频率是仅在带通或带阻滤波器才存在的概念，用${\omega }_{center}$与$f_{center}$表示，对于低通或高通滤波器不存在中心频率的概念。

以带通滤波器为例。带通滤波器有两个截止频率，均是功率降为通带功率0.5倍的频率点，低频率点记为$f_L$，高频率点记为$f_H$。带通滤波器的中心频率指的是通带的中心点，有：
$$\text{中心频率}=\frac{f_H+f_L}{2}$$
同理，带阻滤波器也有两个截止频率，中心频率定义为阻带的中心点，计算公式同上。

5.3 带宽

滤波器带宽指的是通带的宽度，英文BandWidth，记为BW。

对于低通滤波器，通带宽度等于截止频率。

对于高通滤波器，没有带宽的概念。如果是有源高通滤波器，受限与运放的带宽，频率太高的信号是无法通过的，此时高通实际上变为了带通，这时才有带宽的概念。

对于带通滤波器，$\text{带宽}=f_H-f_L$，即两个截止频率的差值。

对于带阻滤波器，不存在通带带宽的概念，只存在阻带带宽的概念。

---

六. 滤波器的增益与衰减

滤波器增益指的是通带内输出幅值与输入幅值的比，用A表示。

对于低通滤波器，增益为传递函数在s = 0这一点的幅值。
$$\text{二阶低通滤波器：}H\left(s\right)=A_m\times \frac{1}{1+n_{1}s+n_2{s}^2}$$

$$A=\left|H\left(0\right)\right|=\left|A_m\times \frac{1}{1+n_{1}0+n_2{0}^2}\right|=\left|A_m\right|$$

对于高通滤波器，增益为传递函数在$s\to \infty$时的幅值。
$$\text{二阶高通滤波器：}H\left(s\right)=A_m\times \frac{s^2}{1+n_{1}s+n_2{s}^2}$$

$$A=\left|H\left(\infty \right)\right|=\left|A_m\times \frac{{\infty }^2}{1+n_1\infty +n_2{\infty }^2}\right|=\left|\frac{A_m}{n_2}\right|$$

对于带通滤波器，增益为传递函数在频率处于两个截止频率[$f_L$, $f_H$]范围内的幅值。可用传递函数在频率为中心频率$f_c$这一点的幅值来表示。
$$\text{二阶带通滤波器：}H\left(s\right)=A_m\times \frac{m_{1}s}{1+n_{1}s+n_2{s}^2}$$

$${\omega }_{center}=\frac{{\omega }_H+{\omega }_L}{2}$$

在中心频率点处，传递函数分母实部为0，所以对于二阶带通滤波器，中心频率=特征频率，有：
$$A=\left|H\left({\omega }_{center}\right)\right|=\left|A_m\times \frac{m_{1}j{\omega }_{center}}{1+n_{1}j{\omega }_{center}+n_2{\left(j{\omega }_{center}\right)}^2}\right|=\left|A_m{m}_1\right|$$

对于带阻滤波器，不存在增益的说法，只会说阻带衰减。其传递函数如下：
$$\text{二阶带阻滤波器：}H\left(s\right)=A_m\times \frac{1+m_2{s}^2}{1+n_{1}s+n_2{s}^2}$$

$$1+m_2{s}^2=0\Rightarrow \omega =1/\sqrt{m_2}$$

显然，分子为0时对应的衰减是最大的，直接衰减到0，但实际情况下，因为元件都不是理想的，衰减永远不可能到真的到0，只能近似到0。

---

七. 滤波器的相移、延时与群延时

输出正弦波和输入正弦波之间，会存在相移，也就相应的存在延时。当输入波形为复合波形，包含多个不同频率的正弦波，且它们的相移没有特殊的规律，就可能出现不同的延时——这会引起输出波形与输入波形形态不同，造成线性失真。

群延时，Group delay，是一个随频率变化的量，用以描述一个滤波器对不同频率的输入信号，产生的延时是否一致。其数学定义是：
$$GD=-\frac{d\phi \left(\omega \right)}{d\omega }$$
即相移对角频率求导的负数。之所以取负数，是因为一般都将延时量定义为正值，而这个延时由小于 0 的滞后相移引起。

对于每一个输入信号来说，滤波器产生的相移与滤波器产生的延时之间存在以下关系：
$$t_{delay}\left(\omega \right)=\frac{\phi \left(\omega \right)}{2\pi }\times T=\frac{\phi \left(\omega \right)}{2\pi f}=\frac{\phi \left(\omega \right)}{\omega }$$
为保证信号不失真，就需要在频率增大时同步增大相移，则延时就会相等。但频率是无限增加了而相移最大就是超前180°或是滞后180°，不能无限增加，所以延时无法一直相等。因此，我们只关心较低频率处的相移与延时特性。

---

八. 滤波器的灵敏度

滤波电路由许多元件构成，每个元件参数值的变化都会影响滤波器的性能。滤波器某一性能指标y对某一元件参数x变化的灵敏度记作Sxy，定义为： $Sxy=(dy/y)/(dx/x)$。

该灵敏度与测量仪器或电路系统灵敏度不是一个概念，该灵敏度越小，标志着电路容错能力越强，稳定性也越高。

---

九. 参考

《ADI新概念模拟电路》—— 4.运放电路的频率特性和滤波器，作者杨建国

《ADI滤波器设计教程》—— ADI智库

---

徐晓康的博客持续分享高质量硬件、FPGA与嵌入式知识，软件，工具等内容，欢迎大家关注。