【笔记】自适应卡尔曼滤波 Adaptive Extended Kalman Filter
·
0 阅读文章
《Adaptive Adjustment of Noise Covariance in Kalman Filter for Dynamic State Estimation》
1 主要内容
一般情况下,kalman中的Q、R都是根据经验、实验或数据手册得到的,但是有些参数是无法获得的,尤其是过程噪声,就需要通过不断试凑确定参数,显然是不靠谱的。
这个文章提供一种自适应调整Q、R的方法,不需要精确的初值,就可以获得较高的滤波精度。
2 思路
2.1 状态方程

2.2 预测

2.3 校正

2.4 Q、R的估计
1)R 的估计

为了使R平滑变化,使用低通滤波。

[16] Online Stochastic Modelling for Network-Based GPS Real-Time Kinematic Positioning
2)Q的估计


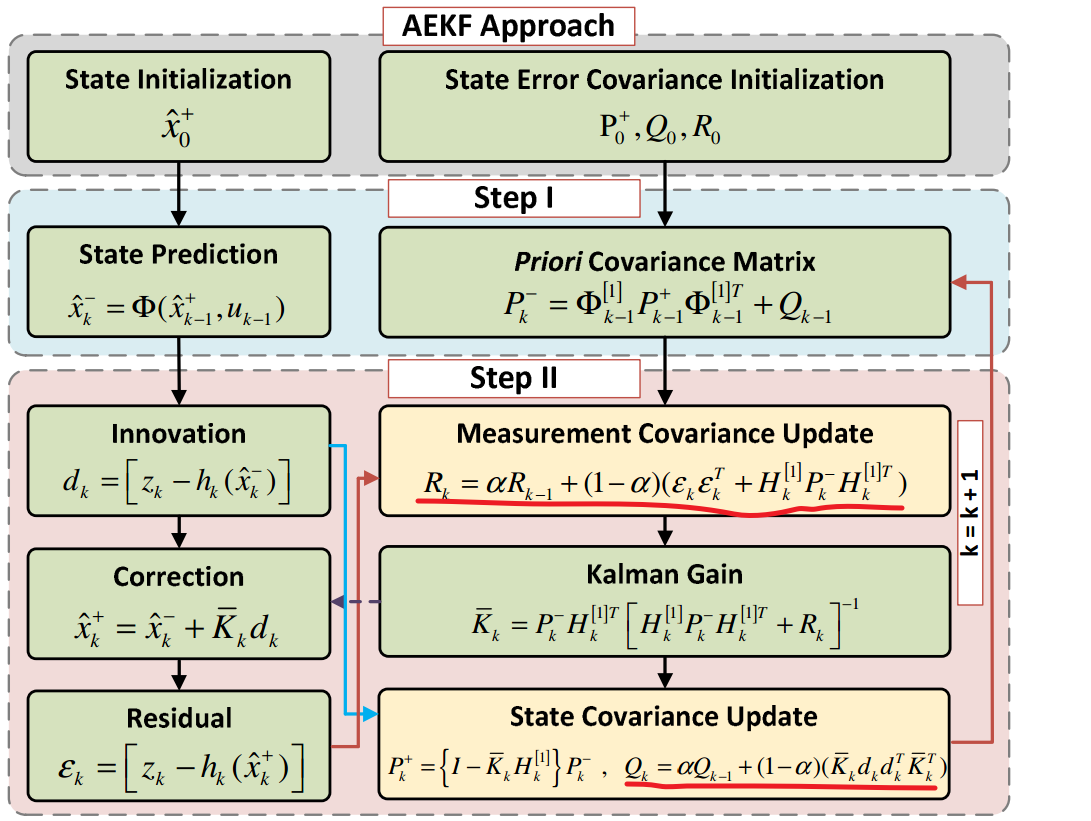
2.5 算法流程图
下图中,划红线地方是相对于常规的EKF增加的部分,也就是测量协方差和过程协方差的更新。

3 仿真实验验证
MSE:mean squared error,计算估计值误差的均方差,用于评定滤波器效果好坏的指标。
下面给出了2个表,第一个是常规的EKF( CEKF),第二个是本文中提到的自适应AEKF。

这个表怎么看呢。Qtrue和Rtrue 分别是Q、R的真值,仿真中把Q、R进行不同比例的缩放,验证不同组合条件下滤波器的精度。
从第1个表,可以得出:
- 只要Q、R的比值和Qtrue、Rtrue相等,就能获得最优的性能,并不需要保证Q、R和真实值接近。
比如,对角线上的值都是相同的。
比如0.1Rtrue、Qtrue和0.01Rtrue、0.1Qtrue的MSE相同,都是0.083。
比如10Rtrue、10Qtrue和Rtrue、Qtrue的MSE相同,都是0.051。
从第2个表,可以看出:
- 不管Q、R的初值是多少,最终的MSE都能取得比较好的效果。
- 相对于CEKF,即使用Q、R的真值,MSE也略大于CEKF中的MSE,这是正常的,因为R、Q会存在波动,并能保证在所有时间都保持和Rtrue、Qtrue比值保持一致。
阅读全文
AI总结
更多推荐
 已为社区贡献3条内容
已为社区贡献3条内容
目录










所有评论(0)