提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

概述

ARIMA （Autoregressive Integrated Moving Average model）–自回归差分移动平均模型，是用于单变量时间序列数据预测的最广泛使用方法之一。AR自回归模型，MA移动平均模型，ARMA自回归移动平均模型都是ARIMA的特殊形式。
ARIMA（p,d,q）模型有3个参数，表示经过d次差分后是平稳的ARIMA（p,q）过程。

---

一、时间序列平稳性

1、严平稳

如果对一切时滞 $k$ 和时点 $t_1、t_2\dots \dots t_n$，都有 $Y_{t_1}、Y_{t_2}\dots \dots Y_{t_n}$与 $Y_{t_1-k}、Y_{t_2-k}\dots \dots Y_{t_n-k}$的联合分布相同，则称序列 {$Y_t$}为严平稳

2、弱平稳

一个序列 {$Y_t$}称为弱（或者二阶矩）平稳，需满足：
（1）均值函数在所有时间上恒为常数
（1）对所有的时间 $t$ 和时滞 $k$，自协方差函数只与时滞有关，与时间点无关，即 ${\gamma }_{t,t-k}={\gamma }_{0,k}$

一般严平稳序列很少满足且不容易证明，通常用弱平稳来指序列的平稳性

二、建模步骤

1.平稳性检验

观察时序图，或者ADF检验判断序列是否平稳。如果平稳直接使用ARMA模型去拟合，如果不平稳但是通过d次差分后是一个平稳过程，使用ARIMA模型拟合。
单位根检验 ADF test

from statsmodels.tsa.stattools import adfuller
adfuller(daytotal['total_purchase_amt'])

原始序列的ADF检验结果为：
(-1.5898802926313504, --------- t 统计量
0.4886749751375929, --------- p值
18, --------- lags used
408, --------- lags used
{‘1%’: -3.446479704252724,
‘5%’: -2.8686500930967354,
‘10%’: -2.5705574627547096}, --------- 置信度对应t值
15960.28197033403)
当 p-value>0.05, 不能拒绝原假设，存在单位根，时间序列非平稳，因此要做差分运算，一般差分1,2 阶就平稳了。除了差分，对数变换或者box-cox变换也是有效的方法。

adfuller(daytotal['total_purchase_amt'].diff(1).dropna())

一阶差分后ADF检验结果为平稳序列，对于ARIMA模型，d值可以选取1

2.人工p 和 q 阶数的确定

样本自相关系数ACF（Autocorrelation function）和偏自相关系数PACF为识别纯AR($p$)或MA($q$)模型提供了有效工具，但是对于混合ARMA模型来说，会有拖尾，识别比较困难

	AR($p$)	MA($q$)	ARMA（$p$，$q$）
ACF	拖尾	滞后q阶后截尾	拖尾
PACF	滞后p阶后截尾	拖尾	拖尾

确定ARIMA的p，q值，绘制一阶差分后序列的自相关和偏自相关图

from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
plot_acf(daytotal['total_purchase_amt'].diff(1).dropna())
plot_pacf(daytotal['total_purchase_amt'].diff(1).dropna())

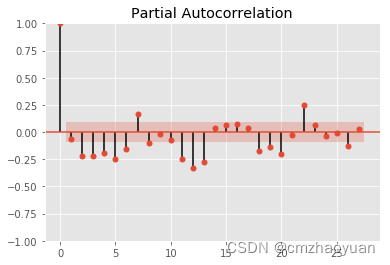
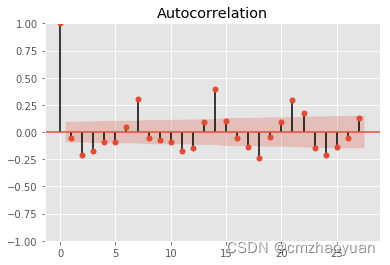
3.模型拟合AIC和BIC确定最优p、q

通过搜索AIC和BIC最小的参数组合，确定p、q。

from statsmodels.tsa.arima.model import ARIMA
import itertools
# 设定参数搜索范围
pmax = 12
qmax = 12
d=1
#
model_eval= pd.DataFrame(columns = ['model','aic','bic'])
for p,q in itertools.product(range(0,pmax),range(0,qmax)):
    model = ARIMA(daytotal['total_purchase_amt'], order=(p,d,q)).fit()
    param = 'ARIMA({0},{1},{2})'.format(p, d,q)
    AIC=model.aic
    BIC=model.bic
    print([param, AIC,BIC])
    model_eval=model_eval.append(pd.DataFrame([[param, AIC,BIC]]))
#排序，选取BIC最小值的参数组合
model_eval.sort_values(by='bic')

根据BIC最小值，确定模型为ARIMA(4,1,10)

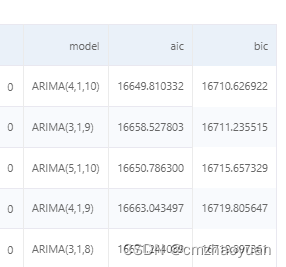
4.模型评价

如果模型被正确识别，并且参与估计充分接近真值，那么残差就应该近似于白噪声。
python使用plot_diagnosis()查看残差图。

from statsmodels.tsa.arima.model import ARIMA
model = ARIMA(daytotal['total_purchase_amt'], order=(4,1,10)).fit()
model.plot_diagnostics(figsize=(16, 12))

1、时序图-------判断是否是有趋势或者季节项。
2、直方图-------拟合曲线看是否是正态分布的形状。
3、QQ图-------看是否在一条直线上。
4、自相关图-------除了在lags=0的时候，在95%的置信区间之外，其他都在置信区间里面。

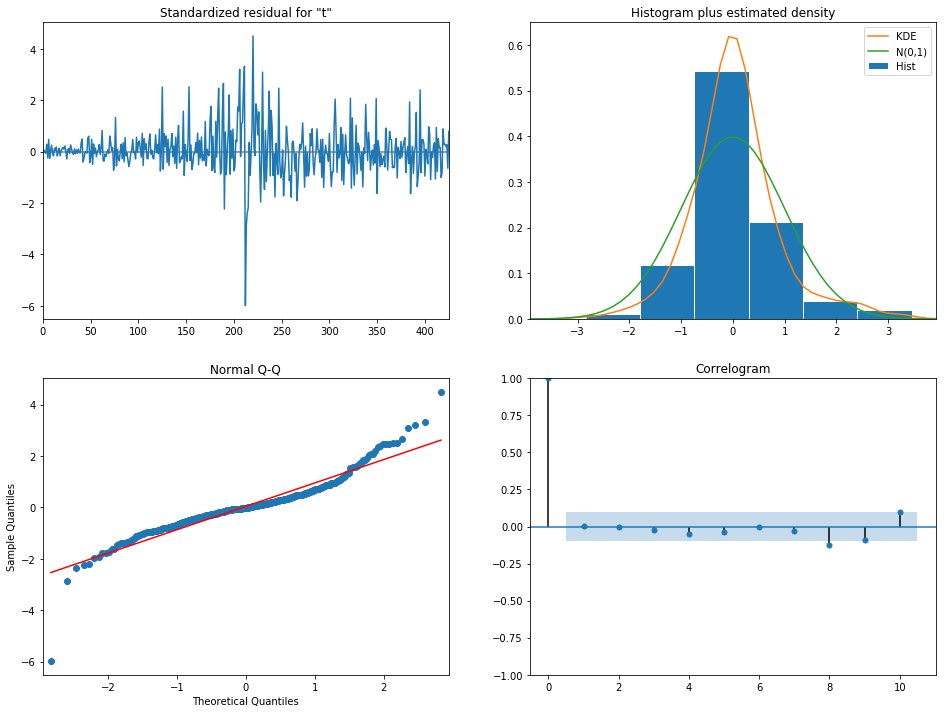
除了观察各个单独的滞后处残差的相关系数，可以使用Ljung-Box统计量混合检验，将这些相关系数的值作为一个组啦进行检验，判断残差自相关性。

from statsmodels.stats.diagnostic import acorr_ljungbox
acorr_ljungbox(model.resid, boxpierce=True)

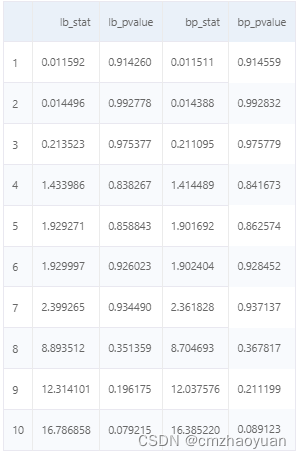
p值都大于0.05，所以没有证据拒绝残差项是不相关的零假设，接受原假设，认为一个残差是一个白噪声序列。

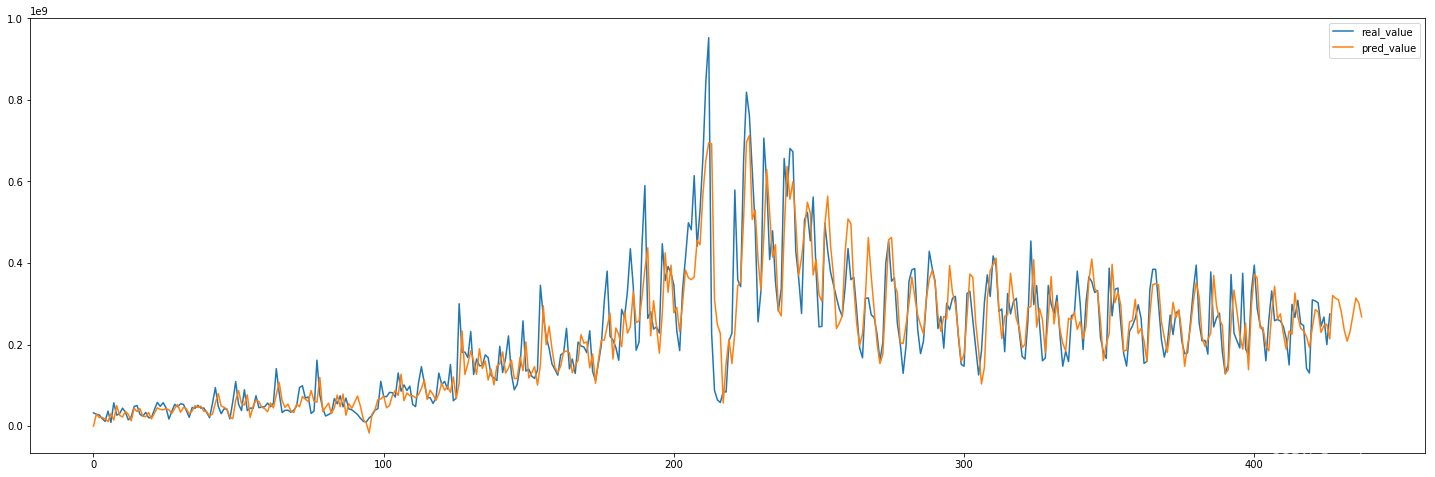
5.模型预测

当模型确定了，预测即等同于外推趋势

ahead=10 # 向前预测多少个值
data=daytotal['total_purchase_amt']
pred_value=model.predict(0, len(data)+ahead) # 预测的第一个数据是0

# 画出拟合图形
plt.figure(figsize=(25,8))
plt.rcParams['font.family']=['SimHei']
plt.plot(data, label='real_value')
plt.plot(pred_value, label='pred_value')
plt.legend()

总结

优点：
ARIMA模型十分简单，只需要考虑序列自身内在的规律，而不需要借助其他外部变量。
缺点：
1、要求时序数据是稳定的，或者是通过差分后是稳定的
2、自回归移动平均，本质上是线性模型，不能捕捉非线性关系