2023-2-20更新：   修改了一些文字错误，优化了排版，增加了一些拓展内容，祝大家学业有成！（期待三连😁😁）

结论： 因子分析与主成分分析是包含与扩展的关系。

   为了能够充分有效的利用数据，化繁为简是一项必做的工作，希望将原来繁多的描述变量浓缩成少数几个新指标，同时尽可能多的保存旧变量的信息，这些分析过程被称为数据降维。主成分分析和因子分析是数据降维分析的主要手段。另一种化繁为简的手段是聚类。

一、 主成分分析

引言：大家都学过线性代数，极大线性无关组的概念想必都很清楚，简单复习一下:一个向量组由多个列向量（或行向量）组成，但组成它的这些列向量之间可能存在某些线性关系（比如有一个列向量是另一个列向量的2倍），那么这样的向量组是不是显得有点臃肿呢？我们对这个向量组进行一些变换（如正交变换）得到一个新的向量组（称为原向量组的极大线性无关组），这个新向量组的列向量个数比原向量组的列向量数量更少，且各个列向量之间线性无关，且原向量组的每一个列向量都可以由这个无关组的向量线性表示。那么，这个极大无关组就可以代表原来的向量组。

   同样的，主成分分析与之有相似的思想，当我们对某个对象进行研究时，往往会收集到与研究对象相关的很多项指标，这些指标之间可能有重复、包含的关系，那么如何对多维的数据进行简化呢？下面就是主成分分析（PCA）要做的事情了。

   主成分分析可以简单的总结成一句话：数据的压缩和解释。常被用来寻找判断某种事物或现象的综合指标，并且给综合指标所包含的信息以适当的解释。

   在实际的应用过程中，主成分分析常被用作达到目的的中间手段，而非完全的一种分析方法。这也是为什么SPSS软件没有为主成分分析专门设置一个菜单选项，而是将其归并入因子分析。我们可以先了解主成分分析的分析模型。

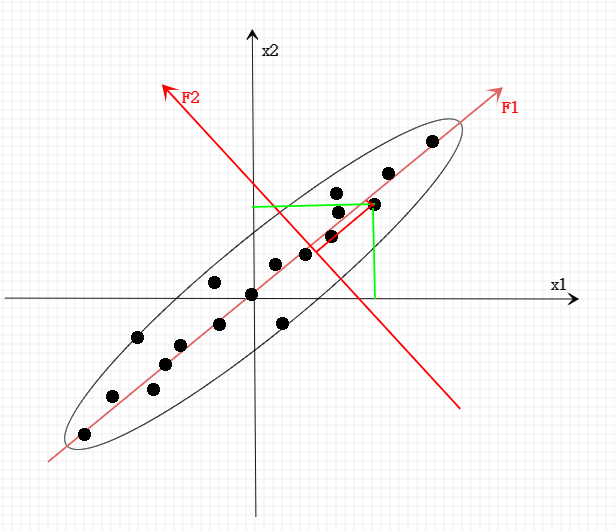
   上面这幅图经常被用来形象地解释主成分分析的原理。图中原来有两个坐标轴$X1$ 和$X2$ ，从散点分布可以很明显的知道散点在这两个坐标轴内存在线性相关关系。

   如果将这些散点在坐标轴 $X1$ 和 $X2$ 上的取值自变量 $x_1$ 和 $x_2$ 纳入到各种回归模型中（也就是说把这些点在原来坐标系下的坐标值带入到模型中去），将会由于它们的多元共线问题（第三节有讲）致使拟合结论出现偏差。那么如何处理才能避免呢？

   这里给大家强调，统计学上数据信息往往指的是数据变异（数据波动）。在上图中，散点的分布构成了一个椭圆形点阵，在椭圆的长轴方向，数据波动明显大于短轴方向。此时如果沿着椭圆的长轴和短轴方向设定新的坐标轴（$F1$ 和 $F2$）组成坐标系，那么新坐标系可以完全解释数据散点的信息，散点在新坐标轴上的取值就形成两个新的变量（$f_1$ 和 $f_2$），这两个新变量之间是相互独立（不相关）。

   从散点图上还可以知道，长轴和短轴能够解释的数据信息是不同的，长轴变量携带了大部分数据的变异信息，而短轴上的变量只携带一小部分变异信息。此时只需要使用长轴方向上的新变量（$f_1$）就可以代表原来两个变量（$x_1$ 和 $x_2$）的大部分信息，达到降维的作用。

   主成分分析的这种坐标轴变化是通过将原来的坐标轴进行线性组合完成的。这个线性组合的过程涉及到线性代数部分的内容，这里不过多解释。

   假设描述对象（例如汽车）由 $k$ 个自变量指标（油耗、车重、轴长、内饰等等）进行描述，因为这些指标很多都是相关的（重量与油耗），因此可以进行主成分分析，浓缩变量。经过坐标轴线性组合以后，可以形成下面的线性组合式子：

$$f_1=a_{11}{x}_1+a_{12}{x}_2+\cdots +a_{1k}{x}_k$$ $$...................................................$$ $$f_k=a_{k1}{x}_1+a_{k2}{x}_2+...+a_{kk}{x}_k$$

   通过线性组合以后，主成分分析可以形成 $k$ 个新变量。这里的线性组合大家可以理解成原来坐标轴的空间旋转，因此原来有多少变量（$k$ 个），经过主成分分析以后，形成数量一致的新变量（$k$ 个）。新变量之间的方差关系见下式，通常情况下，我们只许取前面几个即可。
$$\mathrm{Var}(f_1)>\mathrm{Var}(f_2)>\cdots >\mathrm{Var}(f_k)$$

为什么只取前面几个呢？ 举个例子：10辆汽车，每个汽车取 $k$ 个指标，通过前面的分析，现在形成了 $k$ 个新指标，这 $k$ 个新指标中，每辆汽车的第一个新指标取值之间相差很大，即方差大，那么说明这第一个新的指标可以用来评价者10辆汽车；而第 $k$ 个新指标，10辆汽车取值都差不多，即方差小，那这种指标就没了参考意义。这里的方差你也可以理解为数据变异的程度即波动的大小。 我们要对研究对象进行评价（区分或者排序），就是要研究那些变异大的指标。

---

前面说：对于新变量，我们通常只取前面几个，那么如何取舍呢？且看下文。

   在主成分分析后，SPSS等软件会输出下面这个结果。包括特征根值，方差贡献率和累计方差贡献率。从表格结果可知，原来的变量数量是6个，经过矩阵的线性组合（正交变换）以后，形成了6个新成分，前面2个成分总共贡献了数据变异的73.2%，且特征根都大于1，因此提取了前面2个成分作为主成分。

1. 特征根是矩阵线性组合后的产物，可以看作主成分的重要性指标，代表引入该主成分后可以解释多少原始变量的信息。如果特征根小于1，说明该主成分的解释力度还不如直接引入一个原变量的平均解释力度大，因此一般可以用特征根大于1作为纳入标准。
2. 方差贡献率表示该主成分的方差在全部方差中的比重。这个值越大，表明主成分解释数据信息的能力越强，它与特征根是正相关的，特征根越大，方差贡献率越大。
3. 累计贡献率表示前面n个主成分累计提取了多少数据信息。一般来说，如果前k个主成分的贡献率达到85%，表明提取前面k个主成分就基本可以解释所有数据信息（最低70以上就可以接收，你或许可以增加提取的主成分的数量，但这会降低模型的可解释性，或者你再重新搜集、整理原始指标）。

   主成分分析的一个重要的结论是主成分矩阵，如下表所示。主成分矩阵可以说明各主成分在原来变量上的载荷，所以也被称为载荷矩阵。（载荷矩阵里面的系数代表该变量与该因子的相关性强弱，正、负相关，绝对值越大相关性越强）

   通过载荷矩阵可以写出主成分的组成结构表达式。我们以第一主成分为例，写出其表达式。从式子可以知道，第一主成分包含原来变量1和变量2信息最多，3和5其次，4，6更少一些。这就是主成分分析的致命缺陷，提取出来的主成分不能明确解释成某几个原始变量的概率，为进一步分析制造了困难。（这个问题将由因子分析来解决）

$$F1=0.880X_1+0.868X_2+0.501X_3+0.386X_4-0.599X_5-0.412X_6$$

   主成分分析的另一个结论是主成分得分矩阵。其实就是主成分载荷矩阵除以主成分特征根后得到的矩阵。为什么要除以特征根呢？这是因为主成分载荷矩阵是带有成分重要性属性（包含特征根）的，如果要用提取得到的主成分进行综合排名比较或回归分析，需先要消除主成分的权重不平等（重要性不同），因此需要除以对应主成分的特征根，得到主成分得分矩阵。上表的主成分得分矩阵为：

   根据主成分得分矩阵的得分系数，就可以计算每个个案在新变量（主成分）上的数值。进而可以将新变量值用于综合评分和回归。

$$f_1=0.358x_1+0.353x_2+0.204x_3+0.157x_4-0.244x_5-0.168x_6$$

$$f_2同理$$

   以上就是主成分分析的所有过程。可以通过矩阵变换知道原始数据能够浓缩成几个主成分，以及每个主成分与原来变量之间线性组合关系式。但是细心的朋友会发现，每个原始变量在主成分中都占有一定的分量，这些分量（载荷）之间的大小分布没有清晰的分界线，这就造成 无法明确表述哪个主成分代表哪些原始变量 ，也就是说提取出来的主成分无法清晰的解释其代表的含义。

二、因子分析

   鉴于主成分分析现实含义的解释缺陷，统计学斯皮尔曼又对主成分分析进行扩展。因子分析在提取公因子时，不仅注意变量之间是否相关，而且考虑相关关系的强弱，使得提取出来的公因子不仅起到降维的作用，而且能够被很好的解释。因子分析与主成分分析是包含与扩展的关系。

   首先解释包含关系。如下图所示，在SPSS软件“因子分析”模块的提取菜单中，提取公因子的方法很多，其中一种就是主成分。由此可见，主成分只是因子分析的一种方法。

   其次是扩展关系。因子分析解决主成分分析解释障碍的方法是通过因子轴旋转(在SPSS软件中，旋转的方式有很多种，根据需要选择)。因子轴旋转可以使原始变量在公因子（主成分）上的载荷重新分布，从而使原始变量在公因子上的载荷两级分化，这样公因子（主成分）就能够用那些载荷大的原始变量来解释。以上过程就解决了主成分分析的现实含义解释障碍。

   上面两个表是旋转后的成分矩阵和成分得分系数矩阵，这两个表的数值与主成分分析的结果已经完全不同。从左边的表可以明显知道，第一公因子主要由变量1、2、3（或仅有变量1）解释，第二公因子由变量5、6解释。右边表格的得分系数也不在是通过成分载荷/特征根得到，而是通过回归得出（因为因子分析在提取公因子时，不仅注意变量之间是否相关，而且考虑相关关系的强弱）。

Summarize：

   从以上内容可以知道，主成分分析和因子分析的关系是包含与扩展。当因子分析提取公因子的方法是主成分（矩阵线性组合）时，因子分析结论的前半部分内容就是主成分分析的内容，而因子旋转是因子分析的专属（扩展），主成分分析是因子分析（提取公因子方法为主成分）的中间步骤。这就是为什么很多软件没有专门为主成分分析独立设计模块的原因。从应用范围和功能上讲，因子分析法完全能够替代主成分分析，并且解决了主成分分析不利于含义解释的问题，功能更为强大。

三、多元共线性问题简介

这一节的内容你大致浏览一下就明白了,了解即可。

3.1 多元共线性简介

“多元共线”一词最早由R.佛里希于1934年提出,其最初的含义是指回归模型中的某些自变量是线性相关的,即对于出现在模型中的自变量有关系

成立.其中常数km(m=1,2,…,n)不全为0.称为完全多元共线。

现在所说的“多元共线”有更广泛的含义,除包括完全共线性的情况,也包括变量间有某种关系但又不是十分完全的线性关系.如下式所示的情况

其中ε为随机误差项.此时可称为近似多元共线。

3.2 多元共线性的产生

3.21 由变量性质引起

在进行多元统计分析时，作为自变量的某些变量高度相关，比如身高、体重和胸围，变量之间的相关性是由变量自身的性质决定的，此时不论数据以什么形式取得，样本含量是大是小，都会出现自变量的共线性问题。因此，变量间自身的性质是导致多元共线性的重要原因。

3.22 由数据问题引起

（1）样本含量过小
假设只有两个自变量X1与X2,当n=2时,两点总能连成一条直线,即使性质上原本并不存在线性关系的变量X1与X2,由于样本含量问题产生了共线性。样本含量较小时，自变量容易呈现线性关系。

如果研究的自变量个数大于2,设为X1,X2，…，XP，虽然各自变量之间没有线性关系，但如果样本含量n小于模型中自变量的个数，就可能导致多元共线性问题。

（2）出现强影响观测值
进入20世纪80年代后期,人们开始关注单个或几个样本点对多重共线性的影响。研究表明,存在两类这样的数据点或点群:(1)导致或加剧多重共线性 (2)掩盖存在着的多重共线性。

(a)中因异常观测值的出现而掩盖了共线性;
(b)中因异常观测值的出现而产生了共线性。这样的异常观测值称为多元共线性强影响观测值。显然这种观测值会对设计矩阵的性态产生很大影响,从而影响参数估计。

(3)时序变量

若建模所用的自变量是时序变量,并且是高阶单整时序变量,这种时序变量之间高度相关,必然导致多重共线性。

3.3 多元共线性的影响

以多元线性回归分析为例：采用最小二乘法(the Least Squares Method)对多元线性回归模型的偏回归系数进行估计。（大概介绍一下，不写数学过程了）

1. 如果自变量存在完全多元共线性，无法利用最小二乘法估计偏回归系数。
2. 如果自变量之间存在近似共线性，此时如果仍然采用最小二乘法，会使偏回归系数的估计值不稳定、不合理，严重影响回归模型拟合的效果。

3.4 多元共线性在应用中的表现

（1）模型拟合效果很好，但偏回归系数几乎都无统计学意义；
（2）偏回归系数估计值的方差很大；
（3）偏回归系数估计值不稳定，随着样本含量的增减各偏回归系数发生较大变化或当一个自变量被引入或剔除时其余变量偏回归系数有很大变化；
（4）偏回归系数估计值的大小与符号可能与事先期望的不一致或与经验相悖，结果难以解释。

出现以上表现，提示存在多元共线性问题，应进行多元共线性诊断。这里就不展开说了，已经偏离本文主题了。
复制

3.5 如何解决多元共线性问题

1、从模型中删掉一个变量
2、获取额外的数据或新的样本
3、重新考虑模型
4、参数的先验信息
5、变量变换
6、岭回归
7、主成分回归
8、偏最小二乘回归
9、其它：神经网络、通径分析

---

四、附因子分析案例

本文原本是给大家说明主成分分析和因子分析之间的关系的。并不是教大家如何解决实际问题。可能有些小伙伴看懂了文章，却仍然不知道如何用主成分分析或者因子分析来解决一个实际问题。

今天补充一个案例，案例来源于SPSSPRO软件官方案例。

另外给大家推荐一下这个SPSSPRO软件：https://www.spsspro.com/introduction/

它支持非常多的数据分析模型（算法），还带有一个NoteBook（Python数据分析），每个算法都有文字介绍，还有案例数据，案例视频等，上手难度很小，大家可以用用（对于小白来说，应该比SPPSS这些软件友好）。

---

4.1 案例示例

仅供参考，碎石图、热力图什么的都可以学着放在你的论文中。不过他写的不一定好哦，其中一些说法并不是绝对的，取其精华即可。

根据某地区 2021 年的生产总值、人均可支配收入等多个指标，量化评估多个省市地区的经济发展水平排名或者各指标的权重。（思考：你认为衡量某地经济发展水平，还应该搜集哪些方面的数据？）

4.11 案例数据

因子分析所需数据为若干个定量变量，和一个可选的定类索引项。在本例中，生产总值（亿元）、人均可支配收入（元）、进出口总额（千美元）、财政预算收入（亿元）、工业企业流动资产（亿元）会用于提取因子，而地区则是索引项。

4.12案例操作

1. 新建项目；

2. 上传数据；

3. 选择对应数据打开后进行预览，确认无误后点击开始分析；
   

4. 选择【因子分析】；

5. 查看对应的数据数据格式，【因子分析】要求输入数据为放入 [定量] 自变量 X（变量数 ≥2）;

6. 选择主成分个数、因子旋转方式（注意：在因子分析中倾向于描述原始变量之间的相关关系，所以一般情况下在因子分析选取的主成分个数也就是自变量 X 个数，而特征根选择则是根据设定的阈值为界限，以大于该界限对应的主成分个数作为选取的主成分个数，默认为 1。）;

7. 点击【开始分析】，完成全部操作。

4.13 输出结果

输出结果 1：KMO 检验和 Bartlett 的检验
图表说明:KMO 检验的结果显示，KMO 的值为 0.775，同时，Bartlett 球形检验的结果显示，显著性 P 值为 0.000，水平上呈现显著性，拒绝原假设，即表明各变量间具有相关性，因子分析的结果是有效的，结果可靠程度为一般。

输出结果 2：方差解释表格

图表说明:
上表为总方差解释表格，主要是看因子对于变量解释的贡献率（可以理解为究竟需要多少因子才能把变量表达为 100%），一般都要表达到 90%以上才可以，否则就要调整因子数量。方差解释表中，前两个因子累积解释的贡献率达到 94.296%(一般情况下大于 90%即可)，说明使用前两个因子就能够很好地评估省市地区的经济发展水平。前三个因子则效果更佳，累积解释的贡献率达到 98.921%。

输出结果 3：碎石图

图表说明: 当折线由陡峭突然变得平稳时，陡峭到平稳对应的主成分个数即为参考提取主成分个数。

结果分析：由图可知，从第三个主成分开始，主成分的特征根值开始缓慢的下降，在满足因子累计解释的贡献度达到 90%的情况下，我们可以选择保留三个主成分。

输出结果 4：因子载荷系数表

图表说明: 上表为因子载荷系数表，可以分析到每个因子中隐变量的重要性。 ​

结果分析：第一个因子与生产总值、进出口总额、财政预算收入、工业企业流动资产这四个变量的相关程度较大，可以概括为“地方发展况状”；第二个因子与人均可支配收入这一个变量的相关程度较大，可以概括为“人民富裕程度”。

输出结果 5：因子载荷矩阵热力图

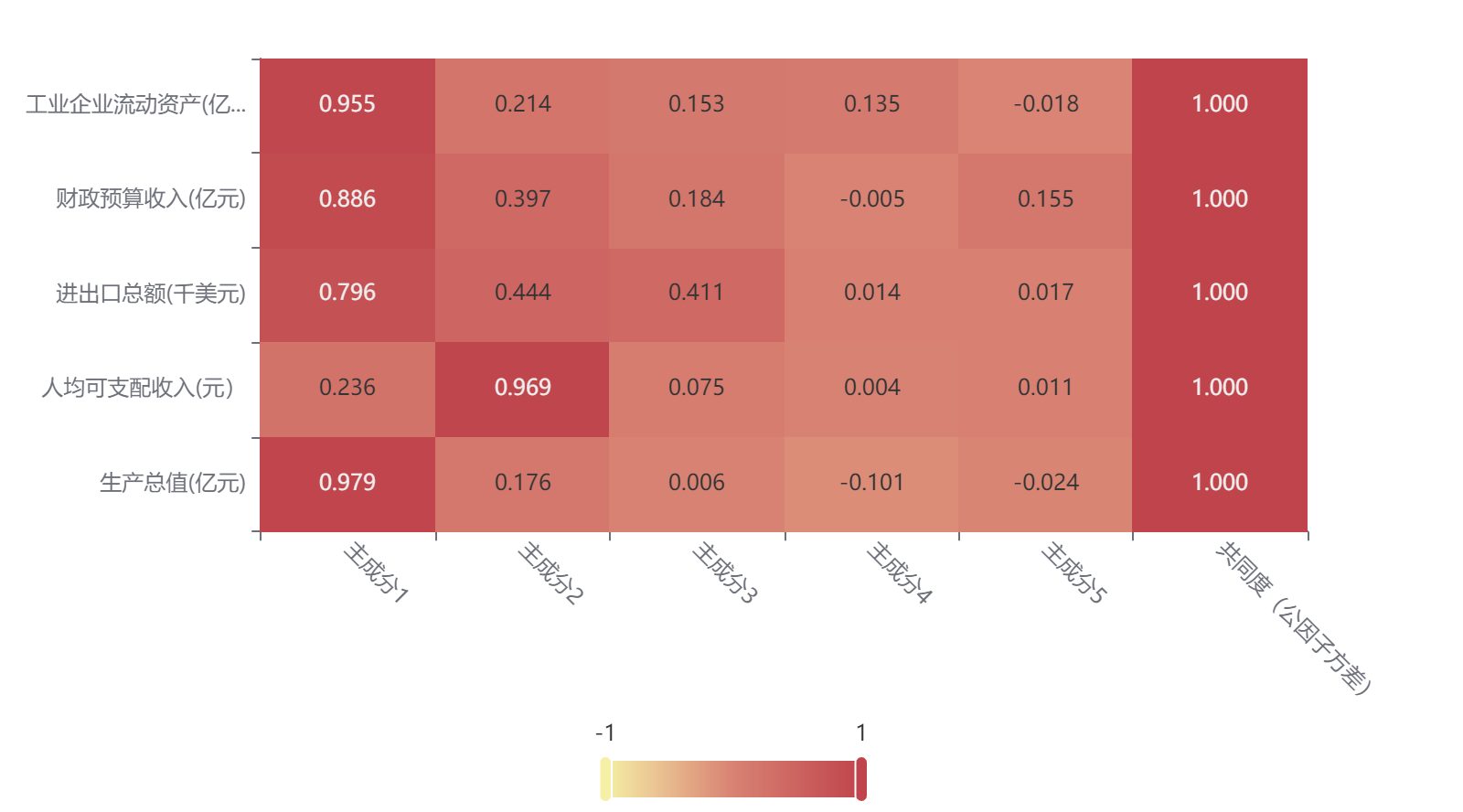
图表说明: 上图为载荷矩阵热力图，可以分析到每个因子中隐变量的重要性，热力图颜色越深说明相关性越大。

结果分析：第一个因子与生产总值、进出口总额、财政预算收入、工业企业流动资产这四个变量的相关程度较大，第二个因子与人均可支配收入这一个变量的相关程度较大。
​

输出结果 6：因子载荷象限分析

图表说明:因子载荷图通过将多因子降维成双因子或者三因子，通过象限图的方式呈现因子的空间分布。当保留两个因子时作出二维因子载荷象限。当保留三个因子时作出三维因子载荷象限。

输出结果 7：成分矩阵表

图表说明: 上表为成份矩阵表，意在说明各个成分的所包含的因子得分系数（主成分载荷），用于计算出成分得分，得出主成分公式。

结果分析：模型的公式：

F1=0.236× 生产总值(亿元)+0.057× 人均可支配收入(元）+0.192× 进出口总额(千美元)+0.214× 财政预算收入(亿元)+0.23× 工业企业流动资产(亿元)
F2=0.244× 生产总值(亿元)+1.348×人均可支配收入(元）+0.618× 进出口总额(千美元)+0.552× 财政预算收入(亿元)+0.298× 工业企业流动资产(亿元)
F3=0.063× 生产总值(亿元)+0.821× 人均可支配收入(元）+4.519× 进出口总额(千美元)+2.024×财政预算收入(亿元)+1.681× 工业企业流动资产(亿元)
F4=-3.888× 生产总值(亿元)+0.164×人均可支配收入(元）+0.517× 进出口总额(千美元)-0.199× 财政预算收入(亿元)+5.176× 工业企业流动资产(亿元)
F5=-1.375× 生产总值(亿元)+0.605× 人均可支配收入(元）+0.94× 进出口总额(千美元)+8.783×财政预算收入(亿元)-1.017× 工业企业流动资产(亿元) 由上可以得到：

F=(0.669/1.0)×F1+(0.274/1.0)×F2+(0.046/1.0)×F3+(0.006/1.0)×F4+(0.005/1.0)×F5

输出结果 8：因子权重分析

图表说明: 上表为因子分析的根据载荷系数等信息所做的主成分权重分析，其计算公式为：方差解释率/旋转后累积方差解释率。

结果分析：因子的权重计算结果显示，因子 1 的权重为 66.9%、因子 2 的权重为 27.396%、因子 3 的权重为 4.625%、因子 4 的权重为 0.576%、因子 5 的权重为 0.503%。
​

输出结果 9：综合得分表

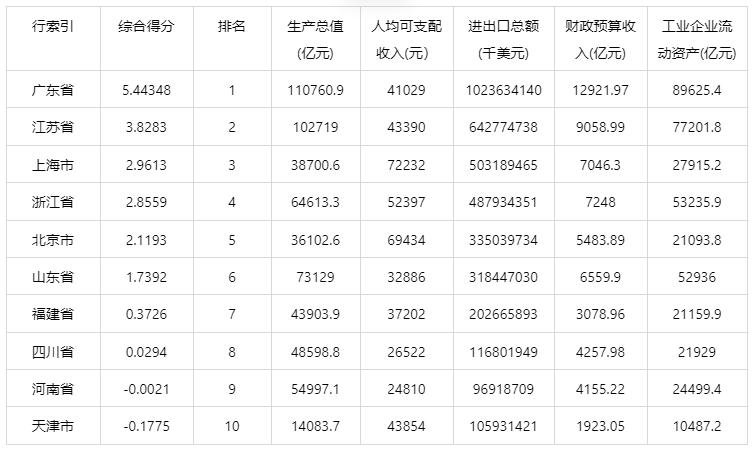
图表说明:综合得分根据F值计算得到的综合得分进行降序排序，可得到各个样本的综合得分与排名情况。

结果分析：由综合得分可知，广东省的综合得分最高，也就是广东省的经济发展水平排名第一，其次是江苏省。

4.14注意事项

• 因子分析要求变量之间的共线性或相关关系比较强，否则不能通过 KMO 检验和 Bartlett 球形检验；
• 因子分析是主成分的推广，相对于主成分分析，更倾向于描述原始变量之间的相关关系（可侧重分析输出结果 4、输出结果 5、输出结果 6）;
• 因子分析时通常需要综合自己的专业知识，以及软件结果进行综合判断，即使是特征根值小于 1，也一样可以提取主成分；
• KMO 值为 null 不存在可能导致的原因为：
   （1）样本量过少容易导致相关系数过高，一般希望分析样本量大于 5 倍分析项个数；
   （2）各个分析项之间的相关关系过高或过低。

---

把 永 远 爱 你 写 进 诗 的 结 尾 ~