
计算几何基础【用图来助你理解几何算法】
计算几何基础1.基本概念1.1计算几何的引入计算几何是几何学的一个重要分支,也是计算机科学的一个分支,研究解决几何问题的算法。在现代工程与数学、计算机图形学、机器人学、VLSI设计、计算机辅助设计等学科领域中,计算几何都有重要应用。计算几何问题的输入一般是关于一组几何物体(如点、线)的描述;输出常常是有关这些物体相关问题的回答,如直线是否相交、点围成的面积等问题。1.2 浮点数造成的误差在学习
写在前面,本人也是小白,这是我在大学自学的内容,有部分内容来自网上,若侵权请告知。当然如果这篇文章能够帮助到你,可以点赞收藏,如果写的不妥的地方,欢迎大佬们指出。
1.基本概念
1.1计算几何的引入
计算几何是几何学的一个重要分支,也是计算机科学的一个分支,研究解决几何问题的算法。在现代工程与数学、计算机图形学、机器人学、VLSI设计、计算机辅助设计等学科领域中,计算几何都有重要应用。
计算几何问题的输入一般是关于一组几何物体(如点、线)的描述;输出常常是有关这些物体相关问题的回答,如直线是否相交、点围成的面积等问题。
1.2 浮点数造成的误差
在学习计算几何之前,我们来回顾一下高中知识,我们求直线方程,或者是交点时,经常出现根号多少多少,以至我们可以直接用根号来表示,但是在我们计算机语言表示时,是需要转化为浮点数的,而浮点数在计算机内部也是按照二进制存取的,大家来思考一下0.3转化为二进制是多少呢?
小数转化为二进制:将小数部分一直做2倍运算,每次取出个位数,直到小数部分没有为止。那0.3=(0.010001100110011…)2是不是求不出精确的啊。计算机会截取前面几位,因此我们在几何题中尽量少用三角函数、除法、开方、求幂、取对数运算,可能要丢失精度。
1.3 如何解决浮点数造成的误差
1.我们在做等于判断时,往往都是直接用== ,但是在计算几何中,判断点,距离,以及弧度制是否相同时,都不能用==,在计算几何中,我们认为误差在1e-6或者更小的范围内是相等的。
2.在输出时一定要注意以下情况,第一不要输出-0.例如a=-0.0001,保留三位小数,第二,在提交几何题的代码时出现RE的情况,acos(1.00001);

1.4 相关定义
点的定义:二维平面下的点的表示只需要两个实数,即横坐标与纵坐标即可。
struct Point{
double x, y;
Point(double x=0, double y=0):x(x), y(y) {}
};
向量的定义:既有大小又有方向的量叫做向量,在计算机中我们常用坐标表示,想一想我们向量是怎么表示的啊,是不是用坐标表示的。
typedef Point Vector;
1.5 向量之间的运算
向量加减法:a=(x1,y1),b=(x2,y2),我们所得到的就是另外一个向量 c=a ± b=(x1±x2,y1±y2).附加:两点相减得到一个向量
向量乘除法:a=(x1,y1),k,向量乘除法就是将向量缩放k倍 ak=(x1 * k,y1k).
向量点积(内积)又称数量积,点积 a ⋅ b=|a| |b| cosθ 设,a=(x1,y1),b=(x2,y2), a ⋅ b =x1 *x2+y1 *y2
几何意义:向量a在向量b的投影a′(带有方向性)与b的长度乘积。
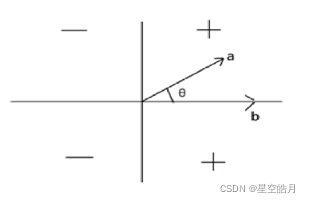
向量叉积(外积)又称向量积,叉积a × b=|a| |b| sinθ,θ表示向量α旋转到向量β所经过的夹角设,a=(x1,y1),b=(x2,y2), |a × b|=x1 *y2-x2 *y1;
几何意义:向量α与β所张成的平行四边形的有向面积
判断外积符号,满足我们高中物理中所学的,右手定则a x b,若b在a的逆时针方向,则为正值,顺时针则为负值。两向量共线或者平行则为0。



2.凸包
2.1凸包定义
在一个实数向量空间V中,对于给定集合X,所有包含X的凸集的交集S被称为X的凸包。X的凸包可以用X内所有点(X1,…Xn)的凸组合来构造.
简单来说:给你一个点集Q,你可以把Q中的每个点想象成一块木板上的铁钉,而点集Q的凸包就是包围了所有铁钉的一条拉紧了橡皮绳所构成的形状;

2.2算法分析
观察凸包我们能发现凸包上的每一个点与它相邻点构成的角都是向左转的;我们把相邻的左转角连成的不封闭图形叫做凸壳(如下图)

图一,图二是凸壳,图三不是凸壳。可以看出求凸包的过程就是一个不断维护凸壳的过程。我们可以借助栈这个结构来维护凸壳。判断矢量a是否在b的逆时针方向:我们就可以用前面所学到的叉积知识,来判断。假设有a,b,c 三个点,我们已知a,b两点是凸壳上的,判断c点是否在凸壳上,等价于判断bc向量是否在ab向量的逆时针方向,如果在就是凸壳上的点,不在就不是。
2.3算法步骤
1.我们要找到最左下角的那个点(作为参照点)
2.对这些点按极角的大小进行排序,如果极角相等的话就按距离远近排序
3.然后我们能确定参照点和第一个被我们排序的点,这两个点肯定是在凸壳上的。然后我们依次枚举剩下的每个点,这里需要用到栈的思想,我们先把凸壳上的两个点压入栈,然后依次将给出的点都压入,每次压入之前判断栈顶的那个点是否是凸壳上的点,如果不是则弹出,否则继续压入后面的点。直到形成凸包。

2.4算法实现

3.直线和线段
3.1相关定义
直线表示常用的有三种形式
- 一般式:ax+by+c=0
- 点向式:x0+y0+vxt+vyt=0
- 斜截式:y=kx+b
计算机中常用点向式表示直线,即参数方程形式表示。直线可以用直线上的一个点P0和方向向量v表示(高数上学过吧),P=P0+vt,其中t为参数
struct Line{
Point v,p;
Line(Point v,Point p):v(v),p(p){}//结构体中的构造函数
Point point(double t){
return v+(p-v)*t;
}
};
3.2判断点是否在直线上 [叉积的运用]
利用三点共线的等价条件α×β==0,直线上取两不同点与待测点构成向量求叉积是否为零。

判断点是否在线段上,就只需要,多判断一个点积,如果PA和PB的夹角为180,就在直线上。

3.3计算点到直线的距离 [叉积的运用]
大家想一想怎样求PO?我们可以借助到ABP形成的平行四边形来计算PO。PO*AB=ABxAP PO=Cross(AB,AP)/Length(AB)


3.4计算点到线段的距离 [点积与叉积的运用]
点到直线的距离也就是求点到直线最短的是吧,那点到线段的距离也是这样,也就是左图的PA就是最短的距离。
思路:判断P是否跨立在AB,如果是,则P到AB的投影在AB线段上,可用前面点到直线的距离求,如果不在,则判断以O为原点判断P在哪个象限,就可以求出最短距离(点积)


3.5计算点到直线上的投影 [点积的运用]
我们可以利用点积公式求出AO长度,然后求出AB长度,已知AB两点的坐标用定比分点来求出O点坐标,也就是A点+AO这段向量即可求出O点。


补充:求P关于AB直线的对称点,我们学了点到直线的投影这就变得简单了,先求出O,然后P’=2*O-P
3.6计算两直线的交点 [叉积的运用]
首先我们在求交点时,我们要保证相交( Cross(AB,CD))的前提下才能求交点。
求O点我们还是用到定比分点的方法。
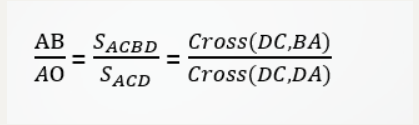


3.7判断两线段是否相交 [叉积的运用]
- 不包括端点

线段AB与CD相交(不考虑端点) 的充分必要条件是
(CA x CB) * (DA x DB) < 0 && (BC X BD) * (AC*AD)<0

- 包含端点

包含端点相交其实也很简单,判断一下四个端点是的相交情况即可。

4.三角形的运用
4.1计算三角形的面积
方法一:
已知三条边(a, b ,c),利用海伦公式S =√(p(p-a)(p-b)(p-c) ), p是三角形半周长 p = (a+b+c)/2
方法二:
已知三个顶点(A,B,C),当然可以用海伦公式求,先算出三条边长。但是有更加巧妙的算法,设三角形三顶点坐标A(xa,ya),B(xb,yb),C(xc,yc),求三角形面积S。
我们前面学过一个公式,叉乘,计算边a和边b构成的平行四边形面积
AB: (xb – xa, yb – ya), BC: (xc – xb, yc - yb);
2 * S = AB X BC = (xb – xa) * (yc - yb) – (yb – ya) * (xc – xb)
S = (xb – xa) * (yc - yb) – (yb – ya) * (xc – xb) / 2;
4.2判断点是否在三角形内部
方法一:叉积法
利用叉积做跨立实验。下面三个条件必须同时满足满足
1.直线PC不能跨立AB
2.直线PB不能跨立AC
3.直线PA不能跨立BC
注:有些题,给的不是三角形。需要提前判断是否为三角形(利用叉积)
方法二:面积法
求▲ABC ?= ▲ APB + ▲ BCP + ▲ ACP
4.3三角形的四心
4.3.1 重心
三条中线的交点
性质一、重心bai到顶点的距离与重du心到对边中zhi点的距离之比为2:1。
性质二、重心和三角形3个顶点组成的3个三角形面积相等。
性质三、重心到三角形3个顶点距离平方的和最小。 (等边三角形)
性质四、在平面直角坐标系中,重心的坐标是顶点坐标的算术平均数,即其坐标为((X1+X2+X3)/3,(Y1+Y2+Y3)/3)
性质五、三角形内到三边距离之积最大的点。
性质六、在△ABC中,若MA向量+MB向量+MC向量=0(向量) ,则M点为△ABC的重心,反之也成立。
4.3.2 外心
三边中垂线交点,到三角形三个顶点距离相同。
1.三角形三条边的垂直平分线的交于一点,该点即为三角形外接圆的圆心.
2三角形的外接圆有且只有一个,即对于给定的三角形,其外心是唯一的,但一个圆的内接三角形却有无数个,这些三角形的外心重合。
3.锐角三角形的外心在三角形内;钝角三角形的外心在三角形外;直角三角形的外心与斜边的中点重合
4.∠BOC=2∠BAC,∠AOB=2∠ACB,∠COA=2∠CBA
5.S△ABC=abc/4R
4.3.3内心
角平分线的交点,
1.内心到三角形三边的距离相同
2.三角形a,b,c分别为三边,S为三角形面积,则内切圆半径r=2S/(a+b+c);
3.如何求内心?A(x1,y1),B(x2,y2),C(x3,y3)
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hBLfB7hP-1648455412848)(C:\Users\xieqi\AppData\Roaming\Typora\typora-user-images\image-20220327202429256.png)]
4.(欧拉定理)△ABC中,R和r分别为外接圆和内切圆的半径,外心和内心的距离为d,则d²= R² -2Rr
4.3.4垂心
三条高线的交点
1.锐角三角形的垂心在三角形内;直角三角形的垂心在直角顶点上;钝角三角形的垂心在三角形外
2.垂心O关于三边的对称点,均在△ABC的外接圆圆上。
3.三角形任一顶点到垂心的距离,等于外心到对边的距离的2倍。
4.锐角三角形的垂心到三顶点的距离之和等于其内切圆与外接圆半径之和的2倍。
等等。。。等考到了自己查。
4.4三角形的费马点
1.该点到三角形三个顶点的距离之和(d)最小。
2.若三角形的三个内角均小于120度,那么该点连接三个顶点形成的三个角均为120度;若三角形存在一个内角大于120度,则该顶点就是费马点。
3.若有一个内角大于120度(这里假设为角C),则距离d为a+b;
若三个内角都小于120度,则距离d为sqrt((aa+bb+cc+4sqrt(3.0)*s/2);
5.多边形
5.1多边形面积
我们可以从第一个顶点除法把凸多边形分成n-2个三角形,然后把面积加起来,最后返回值说为有向面积更贴近本质
double PolygonArea(Point* p, int n) {//p为端点的集合,n为端点个数
double s = 0;
for(int i = 1; i < n - 1; ++i) {
s += Cross(p[i] - p[0], p[i + 1] - p[0]);
}
return s;
}
5.2判断点是否在多边形内

有三种方法,这里讲最简单的两种方法
方法一:
面积法:前面我们说过求多边形面积的方法,然后这里利用叉积
算出点与每条边构成的三角形面积之和是否等于多边形的面积
即可,注:这里算的面积是有向面积。
方法二:
转角法的基本思想是看多边形相对于这个点转了多少度
如果是360°,说明点在多边形内
如果是0°,说明点在多边形外
如果是180°,说明点在多边形边界上
方法三:
射线法…
6.圆
6.1定义
计算机中存储圆通常记录圆心坐标与半径即可
struct Circle{
Point c;
double r;
circle(Point c, double r):c(c), r(r){}
Point point(double a){//通过圆心角求坐标
return Point(c.x +cos(a)*r,c.y + sin(a)*r);
}
};
6.2 圆的应用
6.2.1 点与圆的关系
(1)点P在圆A内(包括在圆周上以及在圆内);
(2)点P在圆A外
求圆心A到P的距离和半径R做比较即可。
AP <= R,则P在内部
AP > R,则P在外部
6.2.2 直线与圆的关系
(1)直线与圆相交
(2)直线与圆相切
(3)直线与圆相离
求点到直线的距离D和半径作比较。
D < R 相交
D = R 相切
D > R 相离
6.2.3求直线与圆的交点
已知圆心c,半径r,和直线的两个点l1和l2,求直线与圆的两个
交点。在计算交点前,必须保证有交点。
现在我们假设已经知道p点,和pp1与pp2的距离,那么我们可以
用定比分法。求出p1和p2.
现在问题转化为求p点,和pp1与pp2的距离。求p点我们在前面已经
学习过了,点在直线上的投影。然后再用勾股定理求出pp1和pp2即可。

补充:
如果求线段与圆的交点,则先求直线与圆的交点,然后再判断点是否在
线段上,这个知识前面我们也学习到了。
6.2.4 圆与圆的关系
1.圆与圆内含:R - r > d
2.圆与圆内切:R- r = d
3.圆与圆相交:R+r > d
4.圆与圆外切:R + r = d
5.圆与圆外离:R + r < d
6.2.5 圆与圆的交点
首先保证必须有交点,也就是圆相交,其次是两个圆心不能重合。圆心a和圆心b
1.两交点的连线必然和两圆心连线垂直。
2.转化为已知ab直线,利用点向式求p1p2直线。然后利用直线与圆的交点来求。

6.2.6 计算圆上到点p最近点,如p与圆心重合,返回p本身
设最近点为cp直线与圆的交点为u和v,u和v其中之一就是最近点,盘点up和vp的距离即可。
求u和v可以直接用定比分法来求。利用点向式,cp方向求出u点,pc方向求出v点。
如果p点和c点重合,则直接输出p点,因为最近点有无数多个。

6.2.7求圆外一点与该圆的公切点
我们都知道,三角形pou和pov是直角三角形,可求po,和∠pou = ∠pov,po的方向向量也能求出,然后让po的方向向量分别向逆时针和顺时针旋转∠pou,这样会得到ou和ov的方向向量,在用点向式求出u和v点。

7.最近点对
7.1问题描述
n个点在公共空间中,求出所有点对的欧几里得距离最小的点对。

暴力求解:O(n²),枚举一个点与其他点的距离,记录最小距离
利用分治思想进行求解。首先分析题目,符合分治法的适用条件,规模越小容易求解,同时具有最优子结构。
7.2分治法求解
1.分解:
对所有的点按照x坐标(或者y)从小到大排序
(排序方法时间复杂度O(nlogn) )。
根据下标进行分割,使得点集分为两个集合。
2.求解:
递归的寻找两个集合中的最近点对。
取两个集合最近点对中的最小值min(dis_left, dis_right )。
3.合并:
最近距离不一定存在于两个集合中,可能一个点在集合A,一个点在集合B,而这两点间距离小于dis。

这其中如何合并是关键。根据递归的方法可以计算出划分的两个子集中所有点对的最小距离dis_left, dis_right ,再比较两者取最小值,即dis= min(dis_left, dis_right ) 。那么一个点在集合A,一个在集合B中的情况,可以针对此情况,用之前分解的标准值,即按照x坐标(或者y)从小到大排序后的中间点的x坐标作为mid,划分一个[mid−dis,mid+dis]区域,如果存在最小距离点对,必定存在这个区域中。
之后只需要根据[mid−dis,mid)左边区域的点来遍历右边区域[mid,mid+dis]的点,即可找到是否存在小于dis距离的点对。但是存在一个最坏情况,即通过左右两个区域计算得到的dis距离来划分的第三区域可能包含集合所有的点,这时候进行遍历查找,时间复杂度仍然和brute force方法相同,都为O(n^2) 。因此需要对此进行深一步的考虑。
1985年Preparata和Shamos具体分析了点在[mid−dis,mid+dis]区域中出现的情况,若(p,q)是Q的最近点对,p在带域左半部分,则q点必在下图所示的d∗2d长方形上,而在该长方形上,最多只能存在6个点使得每个点对之间的距离不小于d,证明如右侧,在d *2d区域上画6个小长方形如图,若存在大于6个点则必有某小长方形上有多于1个点,而这个小长方形最远对角线距离不过5/6 *d,故此区域不可能存在大于6个点.
需要根据[mid−dis,mid)左边区域的点来遍历右边区域[mid,mid+dis]的点,即可找到是否存在小于dis距离的点对。但是存在一个最坏情况,即通过左右两个区域计算得到的dis距离来划分的第三区域可能包含集合所有的点,这时候进行遍历查找,时间复杂度仍然和brute force方法相同,都为O(n^2) 。因此需要对此进行深一步的考虑。
1985年Preparata和Shamos具体分析了点在[mid−dis,mid+dis]区域中出现的情况,若(p,q)是Q的最近点对,p在带域左半部分,则q点必在下图所示的d∗2d长方形上,而在该长方形上,最多只能存在6个点使得每个点对之间的距离不小于d,证明如右侧,在d *2d区域上画6个小长方形如图,若存在大于6个点则必有某小长方形上有多于1个点,而这个小长方形最远对角线距离不过5/6 *d,故此区域不可能存在大于6个点.


计算几何刷题博客总结(某个博主写的,有题解):https://blog.csdn.net/Dream_maker_yk/article/details/80916637
8.计算几何基础算法模板
#include<iostream>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
#define hhh puts("hhh")
#define see(x) (cerr<<(#x)<<'='<<(x)<<endl)
using namespace std;
typedef long long ll;
const int maxn = 1e5+10;
const int mod = 1e9+7;
const double eps = 1e-9;
//求正负符号
int sgn(double d) {
if(fabs(d)<eps) return 0;
if(d>0) return 1;
return -1;
}
//求x,y大小关系,y默认为0
int dcmp(double x, double y=0) {
if(fabs(x-y)<eps) return 0;
if(x>y) return 1;
return -1;
}
struct Point{
double x, y;
Point(double x=0, double y=0):x(x), y(y) {}
};
typedef Point Vector;
Vector operator + (Vector A, Vector B) {return Vector(A.x+B.x,A.y+B.y);}
Vector operator - (Point A, Point B) {return Vector(A.x-B.x,A.y-B.y);}
Vector operator * (Vector A, double p) {return Vector(A.x*p,A.y*p);}
Vector operator / (Vector A, double p) {return Vector(A.x/p,A.y/p);}
bool operator < (const Point &a, const Point &b) {
if(a.x==b.x) return a.y<b.y;
return a.x<b.x;
}
bool operator == (const Point &a, const Point &b) {
if(sgn(a.x-b.x)==0 && sgn(a.y-b.y)==0) return true;
return false;
}
//向量点乘,内积
double Dot(Vector A, Vector B) {
return A.x*B.x+A.y*B.y;
}
//向量叉乘,外积
double Cross(Vector A, Vector B) {
return A.x*B.y-A.y*B.x;
}
//向量长度
double Length(Vector A) {
return sqrt(Dot(A,A));
}
//二维向量夹角,rad值
double Angle(Vector A, Vector B) {
return acos(Dot(A,B)/Length(A)/Length(B));
}
//三角形面积的二倍
double Area2(Point A, Point B, Point C) {
return Cross(B-A,C-A);
}
//向量逆时针旋转rad角度
Vector Rotate(Vector A, double rad) {
return Vector(A.x*cos(rad)-A.y*sin(rad),A.x*sin(rad)+A.y*cos(rad));
}
//向量A逆时针转90°后的单位向量
Vector Normal(Vector A) {
double L=Length(A);
return Vector(-A.y/L,A.x/L);
}
//判断bc是否在ab的逆时针方向,构造凸包时常用
bool ToLeftTest(Point a, Point b, Point c) {
return Cross(b-a,c-b)>0;
}
struct Line{
Point v, p;
Line(){}
Line(Point v, Point p):v(v), p(p) {}
Point point(double t) {
return v+(p-v)*t;
}
};
//求两直线交点,但需保证Cross(v,w)!=0,即两直线不能夹直角
Point GetLineIntersection(Point P, Vector v, Point Q, Vector w) {
Vector u=P-Q;
double t=Cross(w,u)/Cross(v,w);
return P+v*t;
}
//点P到直线AB的距离公式
double DistanceToLine(Point P, Point A, Point B) {
Vector v1=B-A, v2=P-A;
return fabs(Cross(v1,v2)/Length(v1));
}
//点P到线段AB的距离公式
double DistanceToSegment(Point P, Point A, Point B) {
if(A==B) return Length(P-A);
Vector v1=B-A, v2=P-A, v3=P-B;
if(dcmp(Dot(v1,v2))<0) return Length(v2);
if(dcmp(Dot(v1,v3))>0) return Length(v3);
return DistanceToLine(P,A,B);
}
//点P在直线AB上的投影点
Point GetLineProjection(Point P, Point A, Point B) {
Vector v=B-A;
return A+v*(Dot(v,P-A)/Dot(v,v));
}
//判断点P是否在线段AB上,包含端点
bool OnSegment(Point p, Point a1, Point a2) {
return dcmp(Cross(a1-p,a2-p))==0 && dcmp(Dot(a1-p,a2-p))<=0;
}
//判断两条线段是否相交
bool SegmentProperIntersection(Point a1, Point a2, Point b1, Point b2) {
double c1=Cross(a2-a1,b1-a1), c2=Cross(a2-a1,b2-a1);
double c3=Cross(b2-b1,a1-b1), c4=Cross(b2-b1,a2-b1);
//若允许线段在端点处相交,则加入如下if判断,否则不需要
if(!sgn(c1)||!sgn(c2)||!sgn(c3)||!sgn(c4)) {
bool f1=OnSegment(b1,a1,a2);
bool f2=OnSegment(b2,a1,a2);
bool f3=OnSegment(a1,b1,b2);
bool f4=OnSegment(a2,b1,b2);
bool f=(f1|f2|f3|f4);
return f;
}
return sgn(c1)*sgn(c2)<0 && sgn(c3)*sgn(c4)<0;
}
//求多边形面积,p为顶点集合,n为顶点个数
//方法为从第一个顶点出发把凸多边形分成n-2个三角形(另外一个常用的方法就自己写吧)
//顶点应按照逆时针顺序排列!!!关键点
double PolygonArea(Point *p, int n) {
double s=0;
for(int i=1; i<n-1; ++i) s+=Cross(p[i]-p[0],p[i+1]-p[0]);
return s/2;
}
//判断点是否在多边形内(不保证凸多边形)
//若点在多边形内返回1,在多边形外部返回0,在多边形上返回-1
//若要判断在凸多边形内,则只需判断是否此点在所有边的左边
int isPointInPolygon(Point p, vector<Point> poly) {
int wn=0;
int n=poly.size();
for(int i=0; i<n; ++i) {
if(OnSegment(p,poly[i],poly[(i+1)%n])) return -1;
int k=sgn(Cross(poly[(i+1)%n]-poly[i],p-poly[i]));
int d1=sgn(poly[i].y-p.y);
int d2=sgn(poly[(i+1)%n].y-p.y);
if(k>0&&d1<=0&&d2>0) wn++;
if(k<0&&d2<=0&&d1>0) wn--;
}
if(wn!=0) return 1;
return 0;
}
struct Circle{
Point c;
double r;
Circle(Point c, double r):c(c), r(r) {}
Point point(double a) { //通过圆心角求坐标
return Point(c.x+cos(a)*r,c.y+sin(a)*r);
}
};
//求圆与直线的交点,交点存放在sol里面
int getLineCircleIntersection(Line L, Circle C, double &t1, double &t2, vector<Point> &sol) {
double a=L.v.x, b=L.p.x-C.c.x, c=L.v.y, d=L.p.y-C.c.y;
double e=a*a+c*c, f=2*(a*b+c*d), g=b*b+d*d-C.r*C.r;
double delta=f*f-4*e*g;
if(sgn(delta)<0) return 0; //相离
if(sgn(delta)==0) { //相切
t1=-f/(2*e);
t2=-f/(2*e);
sol.push_back(L.point(t1));
return 1;
}
//相交
t1=(-f-sqrt(delta))/(2*e);
sol.push_back(L.point(t1));
t2=(-f+sqrt(delta))/(2*e);
sol.push_back(L.point(t2));
return 2;
}
//两个圆相交的面积
double AreaOfOverlap(Point c1, double r1, Point c2, double r2) {
double d=Length(c1-c2);
if(r1+r2<d+eps) return 0.0;
if(d<fabs(r1-r2)+eps) {
double r=min(r1,r2);
return acos(-1)*r*r;
}
double x=(d*d+r1*r1-r2*r2)/(2.0*d);
double p=(r1+r2+d)/2.0;
double t1=acos(x/r1);
double t2=acos((d-x)/r2);
double s1=r1*r1*t1;
double s2=r2*r2*t2;
double s3=2*sqrt(p*(p-r1)*(p-r2)*(p-d));
return s1+s2-s3;
}
//求解凸包,GrahamScan算法,复杂度nlogn
//顶点编号从0到n-1
//凸包顶点(编号为排序后的编号)保存在stk数组中,从0到top-1
Point lst[maxn];
int stk[maxn], top;
bool cmp(Point p1, Point p2) {
int tmp=sgn(Cross(p1-lst[0],p2-lst[0]));
if(tmp>0) return true;
if(tmp==0&&Length(lst[0]-p1)<Length(lst[0]-p2)) return true;
return false;
}
void Graham(int n) {
int k=0;
Point p0;
p0.x=lst[0].x;
p0.y=lst[0].y;
for(int i=1; i<n; ++i) {
if(p0.y>lst[i].y || (p0.y==lst[i].y&&p0.x>lst[i].x)) {
p0.x=lst[i].x;
p0.y=lst[i].y;
k=i;
}
}
lst[k]=lst[0];
lst[0]=p0;
sort(lst+1,lst+n,cmp);
if(n==1) { top=1; stk[0]=0; return; }
if(n==2) { top=2; stk[0]=0; stk[1]=1; return; }
stk[0]=0, stk[1]=1, top=2;
for(int i=2; i<n; ++i) {
while(top>1&&Cross(lst[stk[top-1]]-lst[stk[top-2]],lst[i]-lst[stk[top-2]])<=0) --top;
stk[top]=i, ++top;
}
}
//三角形
double sqr(double x){
return x*x;
}
double dis(Point a,Point b){ //求ab的长度
return sqrt(sqr(a.x-b.x)+sqr(a.y-b.y));
}
//三角形内心,角平分线的交点,到三角形三边的距离相同
Point Incenter(Point a,Point b,Point c){
double A=dis(b,c);
double B=dis(a,c);
double C=dis(a,b);
double S=A+B+C;
double x=(A*a.x+B*b.x+C*c.x)/S;
double y=(A*a.y+B*b.y+C*c.y)/S;
return Point(x,y);
}
//三条中线的交点,到三角形三顶点距离的平方和最小的点,三角形内到三边距离之积最大的点,重心和3个顶点组成的3个三角形面积相等。
Point gravity(Point a,Point b,Point c){
double x=(a.x+b.x+c.x)/3;
double y=(a.y+b.y+c.y)/3;
return Point(x,y);
}
//三角形外心,三边中垂线交点,到三角形三个顶点距离相同
Point Circum(Point a,Point b,Point c){
double x1=a.x,y1=a.y;
double x2=b.x,y2=b.y;
double x3=c.x,y3=c.y;
double a1=2*(x2-x1);
double b1=2*(y2-y1);
double c1=x2*x2+y2*y2-x1*x1-y1*y1;
double a2=2*(x3-x2);
double b2=2*(y3-y2);
double c2=x3*x3+y3*y3-x2*x2-y2*y2;
double x=(c1*b2-c2*b1)/(a1*b2-a2*b1);
double y=(a1*c2-a2*c1)/(a1*b2-a2*b1);
return Point(x,y);
}
//三角形垂心,三条高线的交点
Point ortho(Point a,Point b,Point c){
double A1=b.x-c.x;
double B1=b.y-c.y;
double C1=A1*a.y-B1*a.x;
double A2=a.x-c.x;
double B2=a.y-c.y;
double C2=A2*b.y-B2*b.x;
double x=(A1*C2-A2*C1)/(A2*B1-A1*B2);
double y=(B1*C2-B2*C1)/(A2*B1-A1*B2);
return Point(x,y);
}
//两条线段的叉积
double crossProduct(double x1, double y1, double x2, double y2) {
return x1 * y2 - x2 * y1;
}
//判断是否点是否在三角形内部
bool isInside(double x, double y, double x1, double y1, double x2, double y2, double x3, double y3) {
//特判是否形成三角形
if (crossProduct(x3 - x1, y3 - y1, x2 - x1, y2 - y1) == 0) {
return false;
}
//注意输入点的顺序不一定是逆时针,需要判断一下
if(crossProduct(x3 - x1, y3 - y1, x2 - x1, y2 - y1) >= 0)
{
double tmpx = x2;
double tmpy = y2;
x2 = x3;
y2 = y3;
x3 = tmpx;
y3 = tmpy;
}
if(crossProduct(x2 - x1, y2 - y1, x - x1, y - y1) < 0) return false;
if(crossProduct(x3 - x2, y3 - y2, x - x2, y - y2) < 0) return false;
if(crossProduct(x1 - x3, y1 - y3, x - x3, y - y3) < 0) return false;
return true;
}
//最近点对模板
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
const int MAXN=1e5+5;
struct Point{
double x,y;
}p[MAXN];
int temp[MAXN];
bool cmpx(const Point &a,const Point &b){
return a.x<b.x;
}
bool cmpy(const int &a,const int &b){
return p[a].y<p[b].y;
}
double dis(int a,int b){//两点之间的距离
return sqrt((p[a].x-p[b].x)*(p[a].x-p[b].x)+(p[a].y-p[b].y)*(p[a].y-p[b].y));
}
double min(double a,double b){//重载min函数
return a<b?a:b;
}
double closestPair(int l,int r)
{
if(r==l) return (1<<30);//只有一个点返回无穷大
if(r-l==1) return dis(l,r);
int mid=(r+l)>>1;
double d1=closestPair(l,mid);//递归左边
double d2=closestPair(mid+1,r);
double d=min(d1,d2);
int cnt=0;
for(int i=l;i<=r;i++)
if(fabs(p[i].x-p[mid].x)<d) temp[cnt++]=i;
sort(temp,temp+cnt,cmpy);
for(int i=0;i<cnt;i++)
for(int j=i+1;j<=i+6 && j<cnt;j++){
if(p[temp[j]].y-p[temp[i]].y>=d) break;
d=min(d,dis(temp[i],temp[j]));
}
return d;
}
int main(){
int n;
while(scanf("%d",&n),n){
for(int i=0;i<n;i++) scanf("%lf%lf",&p[i].x,&p[i].y);
sort(p,p+n,cmpx);//对点进行x轴排序
printf("%.2f\n",closestPair(0,n-1)/2);
}
return 0;
}
//求圆心为(x0, y0), AB两个点的弧长公式
double arc(double x0, double y0, double x1, double y1, double x2, double y2) {
double r,ab,k,b,h,so,C,l,O,s;
r=sqrt((x1-x0)*(x1-x0)+(y1-y0)*(y1-y0));
double r2=(x1-x0)*(x1-x0)+(y1-y0)*(y1-y0);
ab=sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
double ab2=(x1-x2)*(x1-x2)+(y1-y2)*(y1-y2);
double co=(2*r2-ab2)/(2*r2);
O=acos(co);
if(fabs(ab-2*r)<eps)
{
l=PI*r;
return l;
}
else
{
if(O>PI)
O=2*PI-O;
l=O*r;
return l;
}
}
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容








所有评论(0)