实验目的：掌握各种常见的数学统计、数学分析运算的编程实现过程。

实验工具：python

实验内容：
1、随机生成一个10x15的高斯矩阵，均值为自己学号后两位，方差为1。对该矩阵分别进行LU、QR、奇异值，并展示分解结果。

#导入库
import numpy as np
import random

#生成10*15的随机高斯矩阵
a=np.random.normal(loc=50.0,scale=1.0,size = (10,15)) 
print(a)

#SVD分解（奇异值分解）
U,E,V=np.linalg.svd(a)
print(U,E,V,sep='\n\n')

#QR分解
q,r=np.linalg.qr(a)#Python扩展库numpy实现了矩阵QR分解的函数qr()
print(q,r,np.dot(q,r),sep='\n\n')

#LU分解
from scipy.linalg import lu
p,l,u=lu(a)#scipy.linalg.lu函数可以基本实现对Ax=b的LU分解
print(p,l,u,p.dot(l).dot(u),sep='\n\n')#scipy.linalg.lu函数的返回值有三个p'、l'、u',矩阵分解变为(p'l')u' = a

2、利用软件求解优化问题：
min Z = - X1 - 0.8X2 - 1.2X3,
约束：X1 –X2 + X3 <= 30,
3X1 + 2X2 + 4X3 <=42,
3X1 + 2X2 <= 30,
X1, X2 , X3 >=0。
并找到其中有效约束。

#导入sympy包，用于求导，方程组求解等等
from sympy import * 
 
#设置变量
x1 = symbols("x1")
x2 = symbols("x2")
x3 = symbols("x3")
a = symbols("a")
b = symbols("b")
c = symbols("c")

#构造拉格朗日等式
L = -x1-0.8*x2-1.2*x3 + a*(x1-x2+x3-30) + b*(3*x1+2*x2+4*x3-42) + c*(3*x1+2*x2-30)
 
#求导，构造KKT条件
difyL_x1 = diff(L, x1)  #对变量x1求导x1'=-1+a+3b+3c=0
difyL_x2 = diff(L, x2)  #对变量x2求导x2'=-0.8-a+2b+2c=0
difyL_x3 = diff(L, x3)  #对变量x3求导x3'=-1.2+a+4b=0
difyL_a=diff(L,a)  #对a求导
difyL_b=diff(L,b)
difyL_c=diff(L,c)

#求解KKT等式
aa = solve([difyL_x1, difyL_x2, difyL_x3, difyL_a,difyL_b,difyL_c], [x1, x2,x3, a, b, c])
x1=aa.get(x1)
x2=aa.get(x2)
x1=aa.get(x3)
a=aa.get(a)
b=aa.get(b)
c=aa.get(c)

print(aa)
print("最优解为：", -x1-0.8*x2-1.2*x3 + a*(x1-x2+x3-30) + b*(3*x1+2*x2+4*x3-42) + c*(3*x1+2*x2-30))

输出：

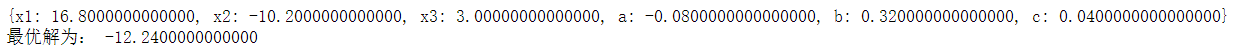
3、对于函数f(x) = (x2-5x+3)exp(-4x)cosx, x = 0: 0.1:1,进行三种方式插值，并将插值曲线与原曲线绘制在同一个Figure窗口。

import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt

x=np.linspace(0,1,11)#x = 0: 0.1:1
print('x=',x)
y=(x**2-5*x+3)*np.cos(x)*np.exp(-4*x)
plt.plot(x,y,"ro")

xnew=np.linspace(0,1,11)#xnew = 0: 0.1:1

for kind in ["nearest","zero","slinear","quadratic","cubic"]:  #"nearest","zero"为阶梯插值#slinear 线性插值#"quadratic","cubic" 为2阶、3阶B样条曲线插值
    f=interpolate.interp1d(x,y,kind=kind)
    ynew=f(xnew)
    plt.plot(xnew,ynew,label=str(kind))

plt.legend(loc="lower right")
plt.show()

输出：


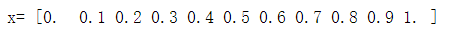
4、统计自己过去12个月实际生活花费的数值，并拟合成一条一次、二次、三次曲线，三条曲线分别用不同颜色和线型展示在同一张图里。

#拟合多项式
import matplotlib.pyplot as plt
import numpy as np

# 需要拟合的数据组
x = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]
y = [2012, 1842, 2345, 1954, 2431, 2321, 2006, 1845, 2030, 1700, 1986, 2064]
plt.plot(x,y,'.')

plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文
plt.rcParams['axes.unicode_minus'] = False    # 用来正常显示负号

z1 = np.polyfit(x, y, 1) #用1次多项式拟合
p1 = np.poly1d(z1) #使用次数合成多项式
y_pre1 = p1(x)
plt.plot(x,y_pre1,label='一次拟合')

z2 = np.polyfit(x, y, 2) #用2次多项式拟合
p2 = np.poly1d(z2)
y_pre2 = p2(x)
plt.plot(x,y_pre2,label='二次拟合')

z3 = np.polyfit(x, y, 3) #用3次多项式拟合
p3 = np.poly1d(z3)
y_pre3 = p3(x)
plt.plot(x,y_pre3,label='三次拟合')
plt.legend() # 显示label
plt.show()

拟合多项式：

# 拟合函数
import numpy as np
import matplotlib.pyplot as plt
from scipy import optimize as op

plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文
plt.rcParams['axes.unicode_minus'] = False    # 用来正常显示负号

# 需要拟合的数据组
x_group = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]
y_group = [2012, 1842, 2345, 1954, 2431, 2321, 2006, 1845, 2030, 1700, 1986, 2064]
plt.scatter(x_group, y_group, marker='o',label='真实值')

# 需要拟合的一次函数
def f_1(x, A, B):
    return A * x + B
# 得到返回的A，B值
A, B = op.curve_fit(f_1, x_group, y_group)[0]
# 画图比较
x = np.arange(0, 15, 0.01)
y = A * x + B
plt.plot(x, y,color='red',label='一次拟合')

# 需要拟合的二次函数
def f_2(x, A, B, C):
    return A * x**2 + B * x + C
# 得到返回的A，B, C值
A, B, C = op.curve_fit(f_2, x_group, y_group)[0]
# 画图比较
x = np.arange(0, 15, 0.01)
y = A * x**2 + B *x + C
plt.plot(x, y,color='blue',label='二次拟合')

# 需要拟合的三次函数
def f_3(x, A, B, C, D):
    return A * x**3 + B * x**2 + C*x + D
# 得到返回的A，B,C,D值
A, B, C, D = op.curve_fit(f_3, x_group, y_group)[0]
# 画图比较
x = np.arange(0, 15, 0.01)
y = A * x**3 + B *x**2 + C*x +D
plt.plot(x, y,color='green',label='三次拟合')

plt.legend() # 显示label
plt.show()

拟合函数：

5、求解三重积分∫（-0.5，1）∫（0，0.5）∫（-0.5pi,pi）(y sinx exp(x)+z cosx x2)dxdydz.

import numpy as np
import math # 导入 math 模块
from scipy import integrate

#三重积分（scipy.integrate.tplquad）,二重积分（scipy.integrate.dblquad），积分（scipy.integrate.quad）
v,err=integrate.tplquad(lambda x,y,z:y*np.sin(x)*math.exp(x)+z*x*x*np.cos(x),-0.5,1,0,0.5,-0.5*np.pi,np.pi)
print(v)

输出：

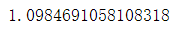
6、求微分方程 xy’+ y – exp(x) = 0,在初始条件y(1) = 2 exp下的特解，并画出解函数的图形。

from scipy.integrate import odeint
import numpy as np
import math
import matplotlib.pyplot as plt

def dy_dx(y,x):
    return (math.exp(x)-y)/x
x=np.linspace(1,10,num=100)
y=odeint(dy_dx,2*math.exp(1),x)

plt.plot(x,y)
plt.grid()
plt.show()

输出：

7、 某人进行射击，及每次命中的概率为0.1，独立射击50次，求击中10次以上且40次以下的概率。

import numpy as np
from scipy import stats
import matplotlib.pyplot as plt

n=50
p=0.1
k=np.arange(n+1)
P=stats.binom.pmf(k,n,p)
print(P)

i=0
p1=0
for i in range(11,40):
    p1+=P[i]
print(p1)

输出：

8、假设自己过去12个月实际生活花费的数值服从正态分布，请求出其均值和方差的极大似然估计。

from scipy.stats import norm
import matplotlib.pyplot as plt
import numpy as np

x_norm =[2012, 1842, 2345, 1954, 2431, 2321, 2006, 1845, 2030, 1700, 1986, 2064]
x_mean, x_std = norm.fit(x_norm)#norm.fit 返回给定数据下，各参数的最大似然估计（MLE）值
print ('mean, ', x_mean)
print ('x_std, ', x_std)

输出：