现代控制理论(1)——状态空间表达式
文章目录前言一、状态变量及状态空间表达式二、状态空间表达式模拟结构图三、状态空间表达式的建立1.由系统框图建立2.由系统的机理建立3.由微分方程或传递函数建立总结前言提示:这里可以添加本文要记录的大概内容:例如:随着人工智能的不断发展,机器学习这门技术也越来越重要,很多人都开启了学习机器学习,本文就介绍了机器学习的基础内容。一、状态变量及状态空间表达式1.状态变量:足以完全表征系统运动状态的最小个
文章目录
一、状态变量及状态空间表达式
1.状态变量:足以完全表征系统运动状态的最小个数的一组变量
x
1
⋯
x
n
x_1\cdots x_n
x1⋯xn
2.状态矢量: 以状态变量为分量构成的矢量
x
(
t
)
=
(
x
1
⋮
x
n
)
x(t)= \begin{pmatrix} x_1 \\ \vdots\\ x_n\\ \end{pmatrix}
x(t)=⎝⎜⎛x1⋮xn⎠⎟⎞
3.状态空间: 以状态变量为坐标轴构成的n维空间
4.状态方程:描述系统
u
u
u与
x
x
x之间关系的一阶微分方程组
x
˙
=
A
x
+
B
u
\dot x=Ax+Bu
x˙=Ax+Bu
5.输出方程:描述系统
y
y
y与
x
x
x之间关系的一阶微分方程组
y
=
C
x
+
D
u
y=Cx+Du
y=Cx+Du
6.状态空间表达式:
x
˙
=
A
x
+
B
u
\dot x=Ax+Bu
x˙=Ax+Bu
y
=
C
x
+
D
u
y=Cx+Du
y=Cx+Du
单输入单输出系统:
x
˙
=
A
x
+
b
u
\dot x=Ax+bu
x˙=Ax+bu
y
=
c
x
y=cx
y=cx
式中
x
x
x为
n
×
1
n\times1
n×1阵,
A
A
A为
n
×
n
n\times n
n×n阵,
b
b
b为
n
×
1
n\times1
n×1阵,
c
c
c为
1
×
n
1\times n
1×n阵
多输入多输出系统:
x
˙
=
A
x
+
B
u
\dot x=Ax+Bu
x˙=Ax+Bu
y
=
C
x
+
D
u
y=Cx+Du
y=Cx+Du
式中
u
u
u为
r
×
1
r\times 1
r×1阵,
y
y
y为
m
×
1
m\times 1
m×1阵
A
A
A为
n
×
n
n\times n
n×n阵,
B
B
B为
n
×
r
n\times r
n×r阵,
c
c
c为
m
×
n
m\times n
m×n阵,
D
D
D为
m
×
r
m\times r
m×r阵
二、状态空间表达式模拟结构图
绘制模拟结构图的步骤:
1、选积分器数目等于状态变量数
2、将每个积分器输出选作一个状态变量
3、据方程画加法器和比例器
三、状态空间表达式的建立
1.由系统框图建立
系统框图->模拟结构图->选定状态变量->建立状态空间表达式
2.由系统的机理建立
3.由微分方程或传递函数建立
对于单变量线性定常系统,可以用一个n阶线性常系数微分方程来描述:
y
(
n
)
+
a
n
−
1
y
(
n
−
1
)
+
⋯
+
a
1
y
˙
+
a
0
y
=
b
m
u
(
m
)
+
b
m
−
1
u
(
m
−
1
)
+
⋯
+
b
1
u
˙
+
b
0
u
y^{(n)}+a_{n-1}y^{(n-1)}+\cdots+a_1\dot y+a_0y=b_mu^{(m)}+b_{m-1}u^{(m-1)}+\cdots+b_1\dot u+b_0u
y(n)+an−1y(n−1)+⋯+a1y˙+a0y=bmu(m)+bm−1u(m−1)+⋯+b1u˙+b0u
相应的传递函数为:
W
(
s
)
=
Y
(
s
)
U
(
s
)
=
b
m
s
m
+
b
m
−
1
s
m
−
1
+
⋯
+
b
1
s
+
b
0
s
n
+
a
n
−
1
s
n
−
1
+
⋯
+
a
1
s
+
a
0
W(s)=\frac{Y(s)}{U(s)}=\frac{b_ms^m+b_{m-1}s^{m-1}+\cdots+b_1s+b_0}{s^n+a_{n-1}s^{n-1}+\cdots+a_1s+a_0}
W(s)=U(s)Y(s)=sn+an−1sn−1+⋯+a1s+a0bmsm+bm−1sm−1+⋯+b1s+b0
(1)当n>m时,传递函数为真分式,状态空间表达式中d=0
(2)当n=m时,长除法,化为整数与真分式之和
W
(
s
)
=
b
m
+
N
(
s
)
D
(
s
)
W(s)=b_m+\frac{N(s)}{D(s)}
W(s)=bm+D(s)N(s)
此时
d
=
b
m
d=b_m
d=bm
3.1能控标准型
1、传递函数中没有零点时
y
(
n
)
+
a
n
−
1
y
(
n
−
1
)
+
⋯
+
a
1
y
˙
+
a
0
y
=
b
0
u
y^{(n)}+a_{n-1}y^{(n-1)}+\cdots+a_1\dot y+a_0y=b_0u
y(n)+an−1y(n−1)+⋯+a1y˙+a0y=b0u
可以直接列写状态空间表达式:

称为能控标准型
2、传递函数中有零点时
y
(
n
)
+
a
n
−
1
y
(
n
−
1
)
+
⋯
+
a
1
y
˙
+
a
0
y
=
b
m
u
(
m
)
+
b
m
−
1
u
(
m
−
1
)
+
⋯
+
b
1
u
˙
+
b
0
u
y^{(n)}+a_{n-1}y^{(n-1)}+\cdots+a_1\dot y+a_0y=b_mu^{(m)}+b_{m-1}u^{(m-1)}+\cdots+b_1\dot u+b_0u
y(n)+an−1y(n−1)+⋯+a1y˙+a0y=bmu(m)+bm−1u(m−1)+⋯+b1u˙+b0u
状态方程与传递函数无零点的状态方程相同
输出方程不同
当n=m时,输出方程为

当m<n时,输出方程为

3.2能观标准型

式中

四、状态矢量的线性变换
令
x
=
T
Z
x=TZ
x=TZ
新的状态空间表达式
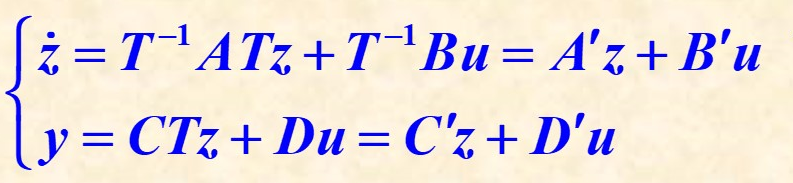
1.状态空间表达式变换为约当标准型
1、无重根时

2、有重根时

重根对应的特征向量的求法

2.当A为友矩阵时
求变换阵T更方便
1、无重根时
变换阵T为范德蒙德矩阵
2、有重根时
变换阵T为:

3.系统的并联型实现(约当标准型实现)
1、具有互异根
展开成部分分式:
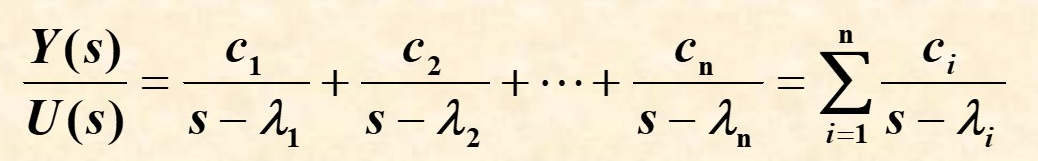
其状态空间表达式如下:

2、具有重根时
假设有三个重根,一个单根
展开成部分分式:

其状态空间表达式如下

五、从状态空间表达式求传递函数矩阵
x
˙
=
A
x
+
B
u
\dot x=Ax+Bu
x˙=Ax+Bu
y
=
C
x
+
D
u
y=Cx+Du
y=Cx+Du
拉普拉斯变换
s
X
(
s
)
=
A
X
(
s
)
+
b
U
(
s
)
sX(s)=AX(s)+bU(s)
sX(s)=AX(s)+bU(s)
Y
=
C
X
(
s
)
+
D
U
(
s
)
Y=CX(s)+DU(s)
Y=CX(s)+DU(s)
假定初始条件为0则有
X
(
s
)
=
(
s
I
−
A
)
−
1
b
U
(
s
)
X(s)=(sI-A)^{-1}bU(s)
X(s)=(sI−A)−1bU(s)
Y
(
s
)
=
c
(
s
I
−
A
)
−
1
b
U
(
s
)
+
d
U
(
s
)
Y(s)=c(sI-A)^{-1}bU(s)+dU(s)
Y(s)=c(sI−A)−1bU(s)+dU(s)
即可求得传递函数矩阵
线性变换不改变系统的传递函数矩阵,同一系统,传递函数阵是唯一的
具有输出反馈的系统如图

其传递函数应等于
W
1
(
s
)
[
1
+
W
2
(
s
)
W
1
(
s
)
]
−
1
W_1(s)[1+W_2(s)W_1(s)]^{-1}
W1(s)[1+W2(s)W1(s)]−1
其中
W
1
(
s
)
W
2
(
s
)
W_1(s)W_2(s)
W1(s)W2(s)分别是前向通道和反馈通道的传递函数
更多推荐
 已为社区贡献7条内容
已为社区贡献7条内容










所有评论(0)