基本概念

二叉树由结点的有限集合构成。
这个有限集合要么是空集，要么是一个根节点及两棵互不相交、分别称为这个跟的左子树和右子树的二叉树组成的集合。

二叉树的特点

1. 每个结点最多有两棵子树，所以二叉树中不存在度大于2的结点。
2. 左子树和右子树是有顺序的，次序不能随意颠倒。
3. 及时树中某结点只有一颗子树，也要区分它是左子树还是右子树。

二叉树的五种基本形态

1. 空二叉树
2. 只有一个根节点
3. 根节点只有左子树
4. 根节点只有右子树
5. 根节点既有左子树，又有右子树

相关概念

边（edge）：两个结点（node）的有序对（order pair），称为边
结点的度：一个节点含有的子树的个数成为该结点的度
叶节点：度为0的结点成为叶节点
路径（path）
路径长度（the length of the paths）
层数：根是第0层（其他结点的层数等于其父节点的层数加1）
深度：层数最大的叶节点的层数

二叉树相关结论

二叉树的存储结构

二叉树的顺序存储结构一般只适用于完全二叉树，通常我们表示二叉树时，都是使用链式存储结构的。

二叉链表

二叉树每个结点最多有两个孩子，所以它有一个数据域和两个指针域。
我们称这样的链表叫做二叉链表。
如图：

lchild	data	rchild

其中data是数据域，lchild和rchild都是指针域，分别存放指向左孩子和右孩子的指针

二叉树的二叉链表结构定义

/*定义二叉树的结构*/
typedef struct Node
{
    char data;                    /*数据域*/
    struct Node *lchild, *rchild; /*左子树和右子树*/
} * BiTree, BiNode;
/*整棵树和结点名称*/

二叉树的遍历

遍历（traversal）
系统地访问数据结构中的结点，使得每个结点都正好被访问一次

深搜有限遍历二叉树：
以下是三种深度优先遍历的递归定义：

前序遍历

规则：若二叉树为空，则操作返回，否则，先访问根节点，然后前序访问左子树，之后前序访问右子树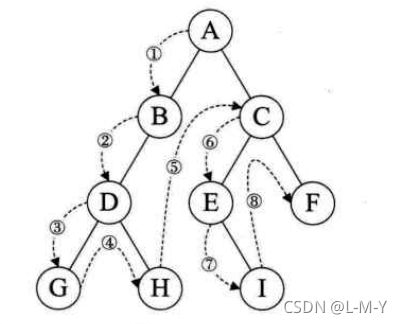

中序遍历

按中序遍历左子树，访问根节点，按中序遍历右子树

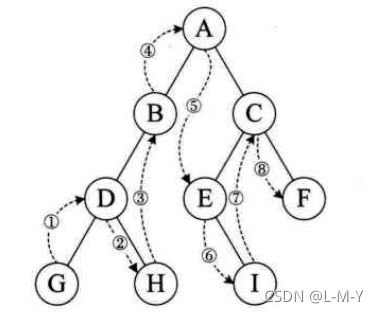
之前看过大佬对中序遍历的解释：把每一个结点都看成一颗颗葡萄，把这些葡萄垂直投影到同一平面上，然后从左到右访问，即为中序遍历。

后序遍历

按后序遍历左子树，按后序遍历右子树，访问根节点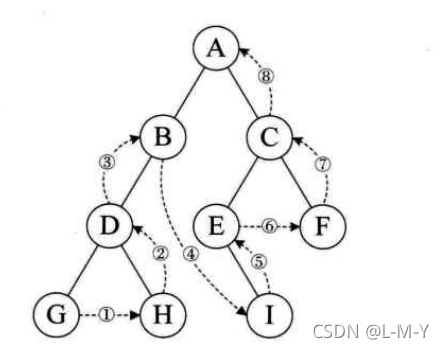

小总结

先序遍历：先根 再左 再右
中序遍历：先左 再根 再右
后序遍历：先左 再右 再根
这个根，指的是每个分叉子树（左右子树的根节点）根节点并不只是整棵树的根节点

代码

#include <iostream>
#include <string>
#include <algorithm>
using namespace std;
/*定义二叉树的结构*/
typedef struct Node
{
    char data;                    /*数据域*/
    struct Node *lchild, *rchild; /*左子树和右子树*/
} * BiTree, BiNode;
/*整棵树和结点名称*/

/*先需创建二叉树*/
void CreateBiTree(BiTree &T)
{
    char ch;
    cin >> ch;
    if (ch == '#')
        T = NULL;
    else
    {
        T = new BiNode; /*创建一个新节点*/
        T->data = ch;
        CreateBiTree(T->lchild);
        CreateBiTree(T->rchild);
    }
    /*递归创建*/
}
void InOrderTraverse(BiTree T)
{
    /*中序遍历*/
    if (T)
    {
        InOrderTraverse(T->lchild);
        cout << T->data;
        InOrderTraverse(T->rchild);
    }
}
void PreOrderTraverse(BiTree T)
{
    /*先序遍历*/
    if (T)
    {
        cout << T->data;
        PreOrderTraverse(T->lchild);
        PreOrderTraverse(T->rchild);
    }
}
void PostOrderTraverse(BiTree T)
{
    /*后序遍历*/
    if (T)
    {
        PostOrderTraverse(T->lchild);
        PostOrderTraverse(T->rchild);
        cout << T->data;
    }
}
/*统计二叉树中结点的个数*/
int NodeCount(BiTree T)
{
    if (T == NULL)
        return 0;
    else
        return NodeCount(T->lchild) + NodeCount(T->rchild) + 1;
}
/*求树的深度*/
int Depth(BiTree T)
{
    if (T == NULL)
        return 0;
    else
    {
        int i = Depth(T->lchild);
        int j = Depth(T->rchild);
        return i > j ? i + 1 : j + 1;
    }
}
/*复制二叉树*/
void Copy(BiTree T, BiTree &NewT)
{
    if (T = NULL)
    {
        NewT = NULL;
        return;
    }
    else
    {
        NewT = new BiNode;
        NewT->data = T->data;
        Copy(T->lchild, NewT->lchild);
        Copy(T->rchild, NewT->rchild);
    }
}
/*统计二叉树中叶子结点的个数*/
int LeafCount(BiTree T)
{
    if (!T)
        return 0;
    if (!T->lchild && !T->rchild)
        return 1;
    /*如果二叉树左子树和右子树皆为空，说明该二叉树根节点为叶子结点，结果为1*/
    else
        return LeafCount(T->lchild) + LeafCount(T->rchild);
}
/*二叉树中从每个叶子结点到跟结点的路径*/
void PrintAllPath(BiTree T, char path[], int pathlen)
{
    int i;
    if (T != NULL)
    {
        path[pathlen] = T->data; /*将当前结点放入路径中*/
        if (T->lchild == NULL && T->rchild == NULL)
        {
            /*若这个节点是叶子结点*/
            for (i = pathlen; i >= 0; i--)
                cout << path[i] << "　";
            cout << "\n";
        }
        else
        {
            PrintAllPath(T->lchild, path, pathlen + 1);
            PrintAllPath(T->rchild, path, pathlen + 1);
        }
    }
}
/*判断二叉树是否为空*/
int BiTree_empty(BiTree T)
{
    if (T)
        return 1;
    else
        return 0;
}
int main()
{
    BiTree T;
    //测试数据AB#CD##E##F#GH###
    cout << "先序遍历输入(以#结束)：";
    CreateBiTree(T);
    cout << "中序遍历输出：";
    InOrderTraverse(T);
    cout << endl
         << "先序遍历输出:";
    PreOrderTraverse(T);
    cout << "\n"
         << "后序遍历输出:";
    PostOrderTraverse(T);
    cout << endl
         << "树的深度:" << Depth(T);
    cout << endl
         << "结点的个数:" << NodeCount(T);
    cout << endl
         << "二叉树中从每个叶子结点到根结点的所有路径：" << endl;
    char path[256];
    int pathlen = 0;
    PrintAllPath(T, path, pathlen);
    return 0;
}

特殊二叉树

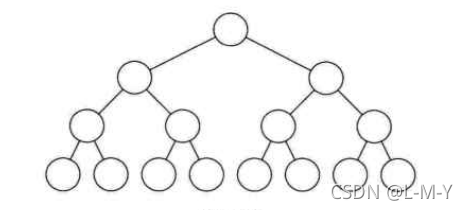
1. 满二叉树
   一颗二叉树中，如果所有分支结点都存在左子树和右子树且左右子树都在同一层上，这样的二叉树成为满二叉树
   如图：
   

2. 斜树
   所有的结点都只有左子树叫左斜树。所有结点都是只有右子树的二叉树叫右斜树。二者统称斜树。（这玩意竖着看其实就是线性表）

3. 完全二叉树
   若一棵有n个结点的二叉树（按照层序规律编号），其中编号为i（1<=i<=n）的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置相同，则这棵树是完全二叉树，如图：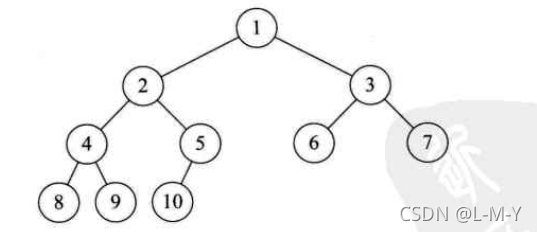

完全二叉树的性质：
1）叶节点只可能在最下两层
2）最下层的叶子一定集中在左部连续位置
3）结点度为 1，则该结点只有左孩子。
4）倒数第二层，如果有叶节点，则一定位于右部连续位置。
5）相同结点的二叉树，完全二叉树的深度最小