c语言请利用两个栈s1和s2来模拟一个队列,考研数据结构之队列(3.3)——练习题之利用两个栈s1和s2来模拟一个队列,然后利用栈的运算来实现队列的enQueue、deQueue及isQueueEmp...
题目请利用两个栈sI和s2来模拟-一个队列,假设栈中元素为int型,栈中元素最多为maxSize。己知栈的3个运算定义如下。push(ST,x):元素x入ST栈。pop(ST,&x):ST栈顶元素出栈,赋给变量X。isEmpty(ST):判断ST栈是否为空。如何利用栈的运算来实现该队列的3个运算:enQueue(元素入队列)、deQueue(元素出队列)、isQueueEmpty...
题目
请利用两个栈sI和s2来模拟-一个队列,假设栈中元素为int型,栈中元素最多为maxSize。己知栈的3个运算定义如下。
push(ST,x):元素x入ST栈。
pop(ST,&x): ST栈顶元素出栈,赋给变量X。
isEmpty(ST):判断ST栈是否为空。
如何利用栈的运算来实现该队列的3个运算: enQueue (元素入队列)、deQueue (元素出队列)、isQueueEmpty (判断队列是否为空,空返回1,不空返回0)。
分析
栈的特点是后进先出,队列的特点是先进先出。所以,当用两个栈sI和s2模拟一个队列时,sI作为输入栈,逐个元素压栈,以此模拟队列元素的入队。当需要出队时,将栈sI退栈并逐个压入栈s2中,sI中最先入栈的元素在s2中处于栈顶。s2退栈,相当于队列的出队,实现了先进先出。只有栈s2为空且sI也为空时,才算是队列空。
代码
核心代码:
/* 入队列 */
/* &s1指的是栈1;&s2指的是栈2;x指的是要入队列的元素 */
int enQueue(SqStack &s1,SqStack &s2,int x) {
int y;
if(s1.top==maxSize-1) { // 若栈s1满,则看s2是为空
if(!isEmpty(s2)) {
return 0;// s1满、s2非空,这时s1不能入栈,s2也不能入栈,因为栈的特点是先进后出
} else if(isEmpty(s2)) { // 若s1满、s2为空,则将s1退栈,将元素压入到s2中
while(!isEmpty(s2)) {
pop(s1,y);
push(s2,y);
}
push(s1,x);// 将栈s1所有元素压入s2中,再将新元素压入s1中,这就实现了元素的入队
return 1;
}
} else {
push(s1,x);// 若s1没有满,则x直接入栈,返回1
return 1;
}
}
/* 出队列 */
/* &s1指的是栈1;&s2指的是栈2;x指的是要出队列的元素 */
int deQueue(SqStack &s1,SqStack &s2,int &x) {
int y;
if(!isEmpty(s2)) { // 栈2不空,则直接出队,返回1
pop(s2,x);
return 1;
} else { // 处理s2空栈
if(isEmpty(s1)) { // 若输入栈也为空,则判定队空,返回0
return 0;
} else { // 先将栈s1倒入s2中,再做出队操作
while(!isEmpty(s1)) {
pop(s1,y);
push(s2,y);
}
pop(s2,x);// 然后s2退栈,实现队出队
return 1;
}
}
}
/* 判断是否队空 */
int isQueueEmpty(SqStack s1,SqStack s2) {
if(isEmpty(s1)&&isEmpty(s2)) {
return 1;// 队列空
} else {
return 0;// 队列不空
}
}
完整代码:
#include #define maxSize 20
typedef struct {
int data[maxSize];// 存放栈中元素,maxSize是已经定义好的常量
int top;// 栈顶指针
} SqStack; // 顺序栈类型定义
/* 初始化顺序栈 */
/* &st指的是要操作的顺序栈 */
void initStack(SqStack &st) {
st.top=-1; // 只需将栈顶指针设置为-1,本栈中将top=-1规定为栈空状态
}
/* 判断栈空 */
/* st指的是要进行判空的顺序栈 */
int isEmpty(SqStack st) {
// 栈为空的时候返回1,否则返回0
if(st.top==-1) { // 判空的条件是栈顶指针是否等于-1
return 1;
} else {
return 0;
}
}
/* 判断栈满 */
/* st指的是要进行判满的顺序栈 */
int isFull(SqStack st) {
// 如果栈顶指针等于maxSize-1那么栈满,否则栈空
if(st.top==maxSize-1) { // maxSize是栈中最大元素个数,已经定义
return 1;// 栈满返回1
} else {
return 0;// 栈空返回0
}
}
/* 进栈 */
/* &st指的是要操作的栈;x指的是要进栈的数据 */
int push(SqStack &st,int x) {
/* 进栈首先要判断栈是否栈满,如果满栈则不能进栈 */
if(isFull(st)==1) {
return 0;// 如果栈满返回0,表示不能进栈
} else {
// 注意:++top和top++在这里的作用是一样的,都可以使用,如果是a=++top和a=top++,那么两个a的值是不一样的,最后top的值还是一样
++st.top;// 先移动指针,再进栈
st.data[st.top]=x;
return 1;// 进栈成功返回1
}
}
/* 出栈 */
/* &st指的是要操作的栈;&x指的是要出栈的数据 */
int pop(SqStack &st,int &x) {
/* 出栈之前要判断栈是否为空 */
if(isEmpty(st)==1) {// 1表示栈空,0表示非空
return 0;// 如果栈空,不能出栈,返回0
} else {
x=st.data[st.top];// 先取出元素,再出栈
--st.top;
return 1;// 出栈成功返回1
}
}
/* 打印栈,从左到右表示栈底到栈顶 */
/* stack表示要被打印的栈 */
void printStack(SqStack stack) {
printf("\n");
for(int i=0; i<=stack.top; i++) {// 注意:data[0]表示栈底元素,data[top]表示栈顶元素
printf("%d\t",stack.data[i]);// 打印栈中元素
}
printf("\n");
}
/* 入队列 */
/* &s1指的是栈1;&s2指的是栈2;x指的是要入队列的元素 */
int enQueue(SqStack &s1,SqStack &s2,int x) {
int y;
if(s1.top==maxSize-1) { // 若栈s1满,则看s2是为空
if(!isEmpty(s2)) {
return 0;// s1满、s2非空,这时s1不能入栈,s2也不能入栈,因为栈的特点是先进后出
} else if(isEmpty(s2)) { // 若s1满、s2为空,则将s1退栈,将元素压入到s2中
while(!isEmpty(s2)) {
pop(s1,y);
push(s2,y);
}
push(s1,x);// 将栈s1所有元素压入s2中,再将新元素压入s1中,这就实现了元素的入队
return 1;
}
} else {
push(s1,x);// 若s1没有满,则x直接入栈,返回1
return 1;
}
}
/* 出队列 */
/* &s1指的是栈1;&s2指的是栈2;x指的是要出队列的元素 */
int deQueue(SqStack &s1,SqStack &s2,int &x) {
int y;
if(!isEmpty(s2)) { // 栈2不空,则直接出队,返回1
pop(s2,x);
return 1;
} else { // 处理s2空栈
if(isEmpty(s1)) { // 若输入栈也为空,则判定队空,返回0
return 0;
} else { // 先将栈s1倒入s2中,再做出队操作
while(!isEmpty(s1)) {
pop(s1,y);
push(s2,y);
}
pop(s2,x);// 然后s2退栈,实现队出队
return 1;
}
}
}
/* 判断是否队空 */
int isQueueEmpty(SqStack s1,SqStack s2) {
if(isEmpty(s1)&&isEmpty(s2)) {
return 1;// 队列空
} else {
return 0;// 队列不空
}
}
int main() {
SqStack stack1,stack2;
initStack(stack1);/* 初始化栈 */
initStack(stack2);
enQueue(stack1,stack2,1);// 将元素1压入栈中
enQueue(stack1,stack2,2);
enQueue(stack1,stack2,3);
enQueue(stack1,stack2,4);
enQueue(stack1,stack2,5);
enQueue(stack1,stack2,6);
int x;
deQueue(stack1,stack2,x);// 出栈
printf("%d",x);
return 0;
}
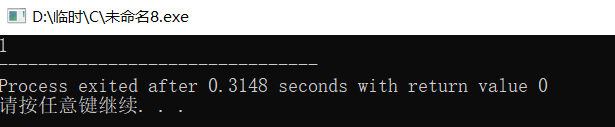
运行结果:
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容









所有评论(0)