NLP学习笔记33-HMM
一 序本文属于贪心NLP训练营学习笔记。本节课开始学习HMM。二 时序类模型常见时序类模型的场景:(沿着时间的维度在变化的,而且数据之间有一定相关性,时间长度不固定)1股票价格、语音、文本,温度的变化。HMM / CRF <= traditional method 传统RNN / LSTM <= deep learning 深度学习三 模型介绍z是状态值(隐式),x是观测值(已知),对
一 序
本文属于贪心NLP训练营学习笔记。本节课开始学习HMM。
二 时序类模型
常见时序类模型的场景:(沿着时间的维度在变化的,而且数据之间有一定相关性,时间长度不固定)
1股票价格、语音、文本,温度的变化。
- HMM / CRF <= traditional method 传统
- RNN / LSTM <= deep learning 深度学习
三 模型介绍
z是状态值(隐式),x是观测值(已知),对应不同时间t有不同的值。是有有方向的、生产模型。

既可以看做判别模型,也可以看做生成模型。
例子:扔不均匀硬币
现在有两个硬币A和B,它们出现正面的概率分别是,让叫小明的人丢硬币,而我只能看到丢的结果,不知道丢的是A还是B。
针对这个例子,我们现在有几个问题:
- 问题1(inference/decoding问题):通过观测到的正反面,小明丢硬币的序列是什么?
- 问题2(parameter estimate问题):
分别是什么?
- 问题3:如果计算某个观测序列出现的边界概率?例如:P(正反正正反)

Part of Speech Tagging(POS) 词性标注例子
观测到的是单词,不知道的是词性。
Q1:维特比解决
Q2:参数估计,再没有标注单词词性的情况下,使用EM算法。

Parameters of HMM :
隐变量 是离散型的(所有数据可以罗列出来),类似于词性标注中的隐状态词性也是有限的。假设其隐状态有m个。
观测变量 不限制,可以是离散型,连续型的。
看下具体的参数
A: transition probability 状态转移概率,是状态
下一个时态转化为
的概率,矩阵大小是m×m
B是emission probability/matrix,就是生成概率矩阵。就在状态下,生成观测变量
的概率。矩阵大小是m×V ,V为观测变量的取值类型,举例的是单词的词典。
对于是连续型的(如语音的波形),是不能写成矩阵的,连续型用高斯混合模型(Gaussian Mixed Model)处理。
: 某一个状态, 在第一个位置的概率

Two Major Tasks
1. 给定模型参数theta, 找出最适合的Z (隐藏状态) Inference / Decoding
2. 估计模型的参数theta
- 1. complete case: 知道x,z => 最大似然估计(MLE)
- 2. Incomplete case: 知道x, 不知道z => EM算法
Case1 Finding best Z (维特比算法)
我们一开始先不看具体的维特比算法。遇到问题的时候,先想一个最笨的方法:
枚举所有可能的隐藏状态组合, 算出概率最高的组合

指数级的复杂度,假设z是3个可能性,序列长度是10,那么可能性就是
维特比算法
对于这种指数级复杂度,使用动态规划算法,就是存储中间状态,避免重复计算。
使用维特比算法的一个前提是,某个隐式状态只和它前后的状态有关,与其他状态无关。
我们是想通过已知条件,x来估计
,可以理解为下面截图的
到
有很多种选择。怎么求出最好的那条连线。
初始概率是有
决定的。另外还有一个因素要从
状态生成观测变量
,因此数学表达就是:
以此类推,那么整根折线的概率就是把上面的概率连乘:
概率越高越好,接下来看如何用DP来简化,就是拆分成子问题来解决。

假设第k时刻,最好的概率.意思是第k时刻最好路径设置为i。
那么第k+1时刻,最好的路径是前一个状态乘上第k+1时刻的概率,加了log操作之后
换句话当前时刻的best score = max(上一个时刻的best score + log当前时刻的转移概率 + log当前时刻的输出概率)
这是一个经典动态规划的场景,每次计算都可以确定出前一个时刻到当前时刻的最佳路径,这样从第一个时刻开始一次向后计算,并把路径结果保存下来就可以求出第k个时刻的最佳路径。

问题2:Forward/Backward Algorithm
这个算法是用来估计:,这个概率可以拆分为:
Forward Algorithm:计算联合概率:
Backward Algorithm:计算条件概率:
前面用了贝叶斯定理,后面用正比于
表示除以p(x) 做一个常数项
接下来看我们用上面的前向x后向展开
前面哪里用了后向公式,因为x的范围1:n,前面只有
,所以还要补上
.
由于和
都是条件独立于
的(意思是
信息都包含在
,可以去掉,原理是D-Seperation定理)
前面一项是Backward Algorithm,后面一项是Forward Algorithm
前面说过是正比于关系,所以在计算的时候要用归一化处理一下

F/B 算法最主要用来计算模型参数
前向算法

算法目标是求:也是利用动态规划的思想来解决这个问题,公式:
这里是把
边缘化 marginalisation,这里缺乏背景知识不懂。
然后是 拆开,目标是:
=
观察式子跟图,找出条件独立的项,根据D-Seperation定理删除掉。
=
式子有3项,第一项是子问题,第二项是矩阵A可得,第三项是 矩阵B可得。我们换个写法:
然后初始条件:
前面有可得,后面有B可得。
后向算法
目标是求:
拆分成子问题:X项,也是跟你前向算法一样,采用边缘化。
第一行到第二行的变化可以乘以验证等价。使用
第一项是子项,第二项可有B可得,第三项可有A可得

时间复杂度是
四 估计模型参数
4.1Complete Case
可以看到x有三个值:abc,z有三个值:123.都是离散的,现在要估计参数。
比较简单:就是根据定义,统计状态转移次数,计算概率。

Incomplete Case
E-steps: 求Z的期望 (theta已知)
M-steps: 最大化 求
,(Z已知) ,不断repeat…until converge(收敛)

简单回归

估计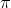
也是用使用哪个FB算法,计算的(期望)次数,再转变为概率。
假定隐变量只有三个状态:1,2,3,也是有3个样本s1,s2,s3。下面截图概率应该是3不是2.8

估计参数B
还是使用FB算法,求出,也是期望值。
假设隐状态有三个:1,2,3
观测值有三个:a,b,c,也要先求出灰色的z,假设已知在参数已知的情况下可以估计概率值.
下面截图的1->a计算数据不对。应该是1.7不是1.4。

估计参数A
这里用到了语言模型bigram的,
,参照这个,见下面截图,分母可用FB算法计算,
接下来看如何求分子。


由于是正比于的关系,不能是直接用,要归一化,记为
例如 求,
,以此类推。
下面看A怎么计算,具体的某一项例如就是把所有的肯能的两两之间状态从1->3的概率之和,见下图

先跟局右上角的 式子计算出所有的概率,计算过程就是统计的过程,使用的是期望的值是浮点数不是整数。
比如,分母是所有状态为1 的概率和(不含最后一列,因为最后一列不会再转移),分子是所有从1->3概率之和。
截图为了表示简洁,只画了状态1的转移概率,还有状态2,3 没有画。

这里例子是最简单,观测值、状态值是离散型的。连续型使用高斯混合模型的没讲。
EM算法限于篇幅,方下一篇整理。
更多推荐
 已为社区贡献9条内容
已为社区贡献9条内容








所有评论(0)